Оглавление:










Применение уравнений макроскопических балансов для решения стационарных задач
- В разделе 10.5 показано, как найти установившийся температурный профиль путем решения различных упрощенных форм хранения. В этом разделе мы покажем, как получить связь между входными и выходными характеристиками стационарной системы потока с использованием макроскопического упрощенного уравнения balance. Оценивая размер отбрасываемых элементов, можно определить в каждом конкретном случае количественный критерий применимости полученных результатов. Приведенные ниже примеры ориентированы на использование уравнений макроскопического баланса для решения некоторых практических задач problems.
Принимая во внимание эти примеры, мы можем лучше понять физический смысл каждого члена в равновесии equation. In примеры 14-2 и 14-3, уравнения макроскопического баланса применяются к части system. It разделен двумя управляющими поверхностями, разделенными небольшим расстоянием друг от друга. Где Cp представлен cal-iol-i — ’c-1, а температура G представлена°C. Газ. Тепло подается на внутреннюю трубуг-14-2, сухой воздух подается из массы воздуха-…*.
Несмотря на большие сложности, возникающие при попытках сформулировать задачу скользящего потока, а во многих случаях именно из-за них существует большое количество работ, освещающих эффекты скользящего потока в газе. Людмила Фирмаль
Температура, давление и линейная скорость воздуха на трубке составляют 148,9°C, 2,04 АТМ и 30,5 мс соответственно* *-_______________••-температура 17,8°C и давление N воздушный поток, размещение Фугасность отвода тепловой энергии-поток считается турбулентным, воздух определяется соотношением (14.14) (14.15)) (ya-ya1)+ 4- [( (14.16) Интеграл формулы (14.16) может быть вычислен по формуле (14.14).После объединения и замены номеров Мистер-Л. Три.. Дж( » Четыре 14-3. Теплообменный аппарат с 2 коаксиальными трубками:1-t горячий газ-TL₁. G-cold холодная жидкость-Гв₁; Получить параметры, количество охлаждающего воздуха.
Как видно из расчета (14.17). Потенциальная энергия、 Пример 14-2 прямоточный и противоточный теплообменник. Необходимо объяснить работу простого теплообменника с 2 коаксиальными трубками Горячие и холодные потоки взаимно противоположны. То есть, если величина u > ₁ или u>2 либо отрицательна. При решении задачи теплообмена можно предположить, что оба потока движутся в полностью развитом турбулентном режиме. Потери тепла в окружающую среду незначительны Поскольку нет потерь тепла в окружающую среду, QT, по предположению= — Qc.
С учетом формул (14.5) и (14.6) при Cp = const установлена зависимость A = CpT для несжимаемых жидкостей и идеальных газов, движущихся под действием не очень больших перепадов давления. Таким образом, формулы (14.19) и (14.20) можно переписать следующим образом: «’Л, л (па-П1)=(?Б 4’ccp. с (Tcₜ-Tₑₗ)= м、 (14.21) (14.22) Уравнение макроскопического баланса энергии в дифференциальной форме. Рассмотрим раздел теплообменника окружении разделах Z и Z + + ДЗ(см. рис.
Примените формулу (14.4) к части, занятой горячим потоком в выбранной области. hCₚ.hdTₕ= dQi、 (14.23) Согласно формуле (13.8), величина dQh может быть заменена формулой K(2π, dg) (Tc-Tn).Где K-суммарный коэффициент теплопередачи, который определяется в соотношении (13.9). в результате для горячего потока: dTₕ ТС-Че ’ К whCp, ч (14.24) в уравнениях по I слагаемым (14.24) и (14.25) получаем уравнение Sp между горячим и холодным потоками любовника*. д [Tₕ-ТК} (14.27) С = ЛГ(2lgb) Вы можете переписать его следующим образом: Qₑ=KAₜ(Tₕ-Tₑ)}ᵣ.
Интегрируем обе части раздела I Выражение (14.27) выражает значение wCₚ для каждого ржавого потока、—— Где Aa обозначает всю внешнюю поверхность внутренней трубки, а значение (GL-Tc) i₀ представляет собой»среднюю логарифмическую разность температур» между двумя потоками. Уравнения (14.28)и(14.29)описывают скорость теплопередачи от горячего потока через стенки теплообменника к холодному потоку и широко используются в инженерной практике. Это расход потока и может быть использован для описания как прямой поток зависимости температуры от координат каждого flow. No. Через Моховую трубу.
Природный газ (почти чистый метан) прокачивается по длинному и длинному трубопроводу с внутренним диаметром 61 см. Газ входит в длину ipP-провода ’ pipeline. At на каждой станции газ снова сжимается и частично охлаждается, так что температура и давление становятся начальными значениями(см. рис.14-4).Рассчитайте затраты на электроэнергию, понесенные на каждой насосной станции, предполагая, что газ идеален и профиль скорости трубопровода везде плоский.
- Отклонения от горизонтального положения трубопровода незначительны. Решение. Полезно решить эту проблему, рассмотрев трубу и компрессор Tdpfferesch.⁰ ₽ ⁰ ⁰ ⁰ ⁰ ⁰ ’Прежде всего, это похоже на выражение Skin^ write (14.10) *Если суммарный коэффициент теплопередачи является переменным, то он учитывается в задаче 14-1.Коэффициент K может сильно изменяться из-за изменения z-координаты ламинарного потока, и результаты, полученные в этом примере, следует использовать с особой осторожностью. (14.30) Благодаря тому, что вся труба достаточно длинная, температура потока может быть разморожена на постоянном уровне, достигая 21,1°C.
Предполагая, что газ идеален、 14-4.Насос сжимаемого газа Трубопровод: Уравнение состояния имеет вид p = pRTIM, а скопический баланс масс, описываемый в виде уравнения (14.30), представляет собой величины p и u. To выразите их вы можете использовать уравнение макроса-pb = piPj для исключения I7 * 1 pdp. 2fdz м о (14.31) Носить (14.33) Шестьдесят один ——————-Для каждого параметра, о котором идет речь,.,….- Вычислять. Кинематика I барометрическое давление и температура 21,1°c составляют 2,67 cps.
Внутренняя энергия запасается вначале в поступательных степенях свободы, и только после достаточного числа столкновений она будет запасаться во вращательных и колебательных степенях свободы. Людмила Фирмаль
Задача состоит в том, чтобы найти 4 неизвестных размера::= P3V3S3, 3, зz и Pz. Поскольку она характеризует происхождение энтальпии, температуру T°можно выбирать произвольно. Если обе части уравнения баланса массы уменьшаются на CPT°и результат вычитается из уравнения баланса энергии для каждого члена, то последнее принимает вид: (£пз «ручьи» + 4-я’}) + У> 2(Ср2 ′ 2 + 4-У3) (14.42) Правые части уравнений (14.39), (14.40) и (14.42) являются известными выражениями и обозначаются через w, P и E. используйте уравнение состояния идеального газа соответственно для исключения из уравнения( 14.40) области давления p и площади поперечного сечения S₃.
Формула (14.32), прибытие После подсчета Мы получаем: Мне нужно отлить Где-W-это рассчитано__________ ………………………это хорошая вещь.» __ К работе компрессора. Подставляя известную величину далее в соотношение (14.36), получаем: ₍₁- ₎₎₎ Яш Яш Яш Яш Яш Яш Яш Яш =(-0.9 + 115)10 «= 1.14-10» эрг г-1 Мощность, необходимая для сжатия газа: (14.37)) nZ> 2 Пиаф (14.40)) «, 3» 3 + P3S3 = «’101 + P1S1 +» > 2″ 2 +p₂s2 С энергией. «>S [£₽(Гз-г») + 4 «J]= u-i [yr (Г1-т т»)±|-«;] + + «’2 (rₛ-т0)+ 4 -» л] (14.41) Добавьте ur к этим уравнениям.
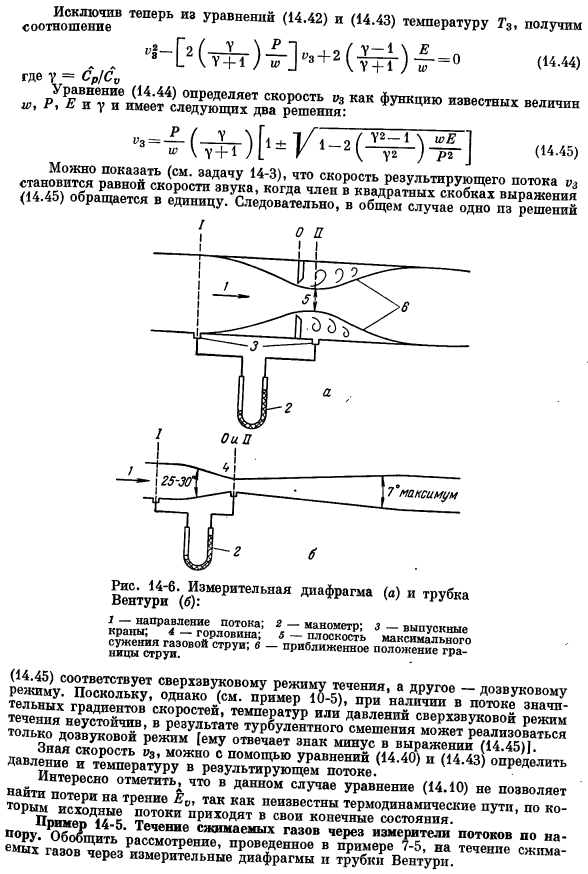
В результате уравнения сохранения импульса описываются следующим образом: Формулы (14.42) и (14.43) температура Г₃、 (Формула (14.44) определяет скорость ’ E и V………………………. Когда член в квадратной скобке bi (14.45) преобразуется в 1, это означает, что скорость результата равна скорости звука(см. задачу 14-3).Поэтому в общем случае 1 па (14.45) соответствует сверхзвуковому потоку, еще 1 соответствует дозвуковому потоку.
Однако если поток имеет значительные градиенты скорости, температуры или давления (см. Пример 10-5), то может быть реализован только дозвуковой режим, поскольку сверхзвуковой режим течения становится неустойчивым в результате турбулентного перемешивания (ему соответствует знак минус 1 уравнения (14.45)). Для определения скорости можно использовать уравнения (14.40) и (14.43). (14.46) Баланс С учетом погрешностей, обусловленных принятием вышеуказанных 3 допущений, был введен так называемый коэффициент потока Cd. Расход должен определяться по экспериментальным данным. При использовании трубки Вентури в качестве качества плоскости II удобно выбрать плоскость минимального сечения (см. рис.
В этом случае выполняется условие Sₐ=Sₒ, в результате чего коэффициенты a,= 1.In кроме того, экспериментально установлено, что коэффициент Cd наиболее равен в сжимаемых и псевдозазорных газах, а в наиболее удачной конструкции Вентури равен 0,98.Когда сжимаемый газ пропускает через измерение Специально для высокообъемной подачи, она чем несжимаемые газы и жидкости. Численное значение коэффициента для измерения диафрагмы также различно[3]. П Именно поэтому формула (14.49) может быть использована в практических целях. Необходимо знать плотность газа как функцию pressure. In другими словами, нам нужно знать уравнение состояния газа и термодинамический путь, по которому газ расширяется.
Опыт показал, что в большинстве случаев расчеты могут производиться исходя из предположения об изоляции расширения и отсутствии эффекта трения. Для идеального газа можно применить уравнение состояния pp = V = const. Где y = Cp / Cv (см. Пример 10-6).Таким образом, без трения теплоизоляция com текущий вид: Формуле(14.49) Эта формула определяет порядок, в котором она может быть измерена, последний для конкретного числа для инженера[31.
Смотрите также:

