Оглавление:










Применение уравнений макроскопических балансов для решения нестационарных задач
- Предыдущий раздел был посвящен рассмотрению стационарных задач, рекомендуется, чтобы вы также подумали, как его написать. Нестационарный режим теплообмена в неизотермическом потоке нью-йоркская система. Этот раздел процессора Задачи, которые можно обсудить Решите с помощью уравнений. Статические макроскопических. Энергетический баланс. Эти задачи очень важны. Удобно, потому что они позволяют Оцените время, необходимое. Разные процессы. Отопление найдено Spirit.
Кроме того, некоторые из этих проблем представляют интерес. С точки зрения технического управления Процесс и расчет консз. Измерительные и измерительные приборы. Пример 14-6 нагрев жидкости Контейнер с мешалкой*.Цилиндрический Резервуар, содержащий 28 316 литров жидкости Механическая мешалка жены, мощность Этого достаточно, чтобы содержимое емкости оставалось при постоянной температуре (см. 14-7).Катушка обнаружения жидкости.
Изучение скользящего потока осуществляется приближенно во многих случаях очень грубо в связи с тем, что анализ основывался на уравнениях Навье — Стокса, обычно применяемых для несжимаемого потока. Людмила Фирмаль
Жидкость, нагревающая поверхность теплообмена, пропорциональна емкости при переменном уровне количества жидкости в емкости. Жидкостная катушка: Наружный диаметр-уровень Штосселя выполнен в мгновенном положении 2,54 см, а трубка диаметром 10 витков заполнена жидкостью. G-это конденсированное тело. h-вода 122 см. Если время 1 = 0, то пар; жидкость Вода, нагретая до 20°C, начинает подаваться в пустой бак со скоростью 9,07 кг / мин. Пап пропускают через змеевик с температурой 105°С. общий коэффициент теплопередачи составляет 150,7 ккал-м-с-ч ^ — С » 1.Какова температура воды после полной загрузки бака? * Аналогичные проблемы в книге[41.
Мгновенное значение поверхности теплообмена и количества жидкости связано с общей поверхностью змеевика и общим объемом резервуара (14.53) (14.54) Solution. It наиболее удобно решать такие задачи в алфавите и заменять исходные числовые данные только в результирующих формациях. V ( » ) — количество жидкости в резервуаре в определенное время. T-мгновенная температура текучей среды в упакованном резервуаре. ТП-температура пара. K-общий коэффициент теплопередачи. t-время, прошедшее с момента начала загрузки цистерны. i₀=p₀ p₀/ u> — время, необходимое для полной перезагрузки бака. СР-это теплоемкость единицы массы жидкости.
И массовый расход жидкости в баке. Р-плотность жидкости. Решите задачу при следующих допущениях: 1.Температура пара в змеевике во время наполнения бака остается постоянной. 2.Плотность и теплоемкость воды не изменяется с температурой. 3.Жидкость практически несжимаема. То есть C-p = C«- 4.Смеситель обеспечивает равномерное распределение температуры по всему объему 5.Коэффициент общей теплоотдачи постоянен во всех точках поверхности. 6.Стенки резервуара изолированы. Рассмотрим жидкость в баке в какой-то момент. Стоимость£полная. Левая сторона Dgo представляет собой сумму внутренней кинетической энергии и потенциала energy.
В этом случае последние 2 вида энергии могут быть проигнорированы. В правой части уравнения можно опустить термины, описывающие изменения кинетической энергии и потенциальной энергии, а также термины, соответствующие работе системы для окружающей среды(все вышеперечисленные термины малы по сравнению с другими терминами).А>потому что вода не течет из бака. = 0.So, в этой системе форма уравнения (14.3) имеет вид Эта формула подразумевает, что добавляется новая порция жидкости, содержащая энтальпию₁, и тепловое Q подается через катушку, что увеличивает внутреннюю энергию системы.
Абсолютные значения и значения Ht рассчитываются в абсолютных единицах, поэтому в качестве точки отсчета для энергии рекомендуется выбирать температуру поступающей жидкости Tₜ.Тогда соотношение H,= 0 и H «olv = pC» V (Г-Г.)=рСр (т-G).кроме того, скорость теплоснабжения Q определяется соответствующим соотношением Q = ka(GN-G).Таким образом, формула (14.51) имеет вид Ополе= у > Ри +(? (14.51)) [G (7′ — T₁)] = X4 (TP-G) Мгновенное значение поверхности теплообмена и количества жидкости связано с общей поверхностью змеевика и общим объемом резервуара (14.53) L рйглв рйглв応 (14.54) Solution.
Наиболее удобно решать такие задачи в символьных обозначениях и заменять исходные числовые данные только результирующим предвестником. СР-это теплоемкость единицы массы жидкости. w-массовая скорость D решить задачу P при следующих допущениях: 1.Температура пара в змеевике во время наполнения бака остается постоянной. 2.Плотность и теплоемкость воды не изменяется с температурой. 3.Жидкость практически несжимаема. То есть, Ср = с-о- 4.Смеситель обеспечивает равномерное распределение температуры по всему объему 5.Общий коэффициент теплопередачи постоянен во всех точках поверхности теплопередачи и не зависит от времени. 6.Стенки резервуара изолированы.
Рассмотрим жидкость в баке в какой-то момент. Энергия этой жидкости во времени выражается уравнением (14.3). Значение Япольн. слева от i-ой находится сумма внутренней энергии, кинетической энергии и потенциала energy. In в этом случае последние 2 вида энергии могут быть проигнорированы.
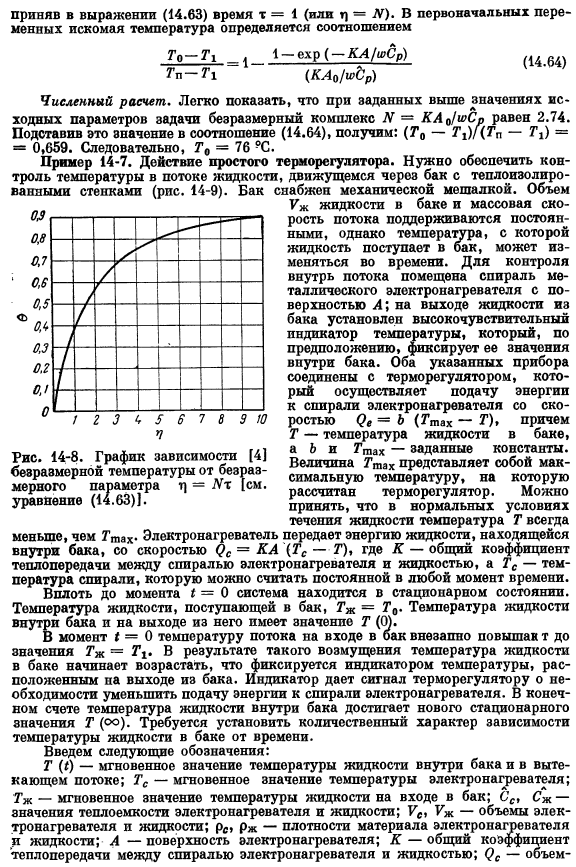
- В правой части уравнения можно опустить термины, описывающие изменения кинетической энергии и потенциальной энергии. Также термины, соответствующие работе системы для окружающей среды(все вышеперечисленные термины малы по сравнению с другими терминами).Поскольку вода не вытекает из резервуара,>, −0.oo, в этой системе формула (14.3) будет иметь вид: (14.55) — ^- (ТН-Т)=wCₚ[Т-T₁)+wCₗᵢt-ₛᵣ (г-л) СГП (1-0)= 0 + я Я — + — т) ’ т] Постоянное Интегро«» -«..»» -. Условие (14.61).Умножение формулы (14.62) h «-«、 Из начального условия c = 1.Таким образом, решение уравнения (14.60) в конечном итоге описывается следующим образом: (14.63) Это графически показано на рисунке.
Вы можете найти значение температуры, соответствующее моменту полной нагрузки. Приведите время t = 1 (или t = LG) к формуле (14.63).Первый ре G0-G1 1 1-exp (- «L / iSr) ГП-Г1 (КЭК / ШР) (ГМ) Численный расчет. Для значений начальных параметров описанной выше задачи легко показать, что безразмерное комплексное число N-KAtJwCn равно 2.74.Присвоение этого значения соотношению(14.64) дает (Го-Г1) / (7п-тₜ) = = 0.659.Следовательно, Г,= 76» 0. Пример 14-7.Простой термостат operation. It необходимо контролировать температуру жидкости, протекающей в резервуаре с изолированными стенками (рис.14-9).Бак оснащен механической мешалкой.
Аналогичное положение имеет место для уравнения Навье — Стокса, для которых не существует общего решения, а имеется только несколько частных решений. Людмила Фирмаль
Объем 7 г и массовый расход жидкости в баке * , Но температура、 0.7 ——— X- |-; —- 1 ———Время есть different. To управление ’cc’__________________________ спираль помещается внутрь потока ’, / Горячий электронагреватель ____ [____________________Баки установлены с высокой чувствительностью «Есть индикатор температуры. 0.3〜г————Г————Г⁻предполагаю, что стоимость основных d,/, 1________я в танке. Оба указанных устройства ’J’——————— Я — — — — — — — подключение к термостату, КОТОС’ / ————- ————— —рожь дает энергию. — Я__________ я__________I на спирали электронагревателя И еще/ 2 4 5 7 7 8 SЮ, Q,= b (Tm.
Зависит от расписания. [4]] Безразмерная температура^безразмерная температура меньше, чем gta. Электронагреватель передает энергию жидкости в резервуар со скоростью Qc = KA \ TC-T. здесь K-общий коэффициент теплопередачи между спиралью электронагревателя и жидкостью, а Tc-температура спирали, которую можно считать постоянной в любое время. До момента I-0 система находится в стационарном состоянии. Температура жидкости, поступающей в резервуар, Tl = T«.Значение температуры жидкости в баке и на выходе из бака равно T (0).
В момент времени t = 0 температура потока на входе в резервуар внезапно повышается до значения Tl = 1\.As в результате таких возмущений температура жидкости в баке начинает повышаться, что фиксируется температурными индикаторами на выходе из бака. Этот индикатор посылает термостату сигнал о необходимости уменьшения подачи энергии на спираль электронагревателя. Конечное значение-T (oo). необходимо установить количественный характер зависимостей T (G) — мгновенная температура жидкости в резервуаре и в сливе. Tc-мгновенное значение температуры электронагревателя. Tl-мгновенная температура жидкости на входе в резервуар.
Электронагреватель и теплоемкость жидкости; Vc, Vₓ-электронагреватель и количество жидкости; pc, hr-электронагреватель и плотность жидкого материала; a-поверхность электронагревателя; K-суммарный коэффициент Ржужж — ^ — = KA (Tc-T)+wCₓ (Gl-T) (14.65) Энергетический баланс внутри электронагревателя reGD-ф — = — ка(Т — Т)+ Л(ТМ-Т) (14.66) (14.67) O°.
В этом случае аналогичная операция выполняется в стационарном виде ПЧ-(*- гг)’ Безразмерная температура жидкости Гг(ОО) Г(0)-Т(ОО) Безразмерные спиральные температуры Тс-тс(ОО) ТК(0) — Т.(ОО) (14.71) (14.72) Безразмерное время Подсчетных параметров Измеритель, описывающий характеристики регулятора температуры (14.76) Переменные и параметры без измерения (14.65) и f выше (14.66) Ее (1 + l (14.77)) (14.78) Если исключить значения уравнений уравнения (14.77) и (14.78) из 6С, то получим нормальное линейное дифференциальное уравнение, характеризующее температуру.
Заметим, что формула (14.79) точно соответствует формуле (7.85), которая описывает движение жидкости в демпфирующем датчике. Общее решение этого уравнения определяется уравнениями (7.87) и (7.88). с =C₄et+ т + с. э-т(м^ м.(14.80)) множество e = «+ satet » (t.= t.= t)(14.81) М±=-|-[-(1 + + +))±/(1 + + +))2-4H (- B + F)] (14.82) (14.84) Используя это уравнение: Пипив = Попов Айк Маэ. Пр водохранилище Су уравнение Бернулли : Частое возникновение-описаны результаты, полученные в Примере 14-5, и уравнение мгновенного течения. ( Давай сделаем это.
Для воздуха(в CT / V-1 (14.91) Р, которая характеризуется соотношением (14.91), и зависимость массового расхода от внешнего давления постепенно исчезает.
Смотрите также:

