Оглавление:


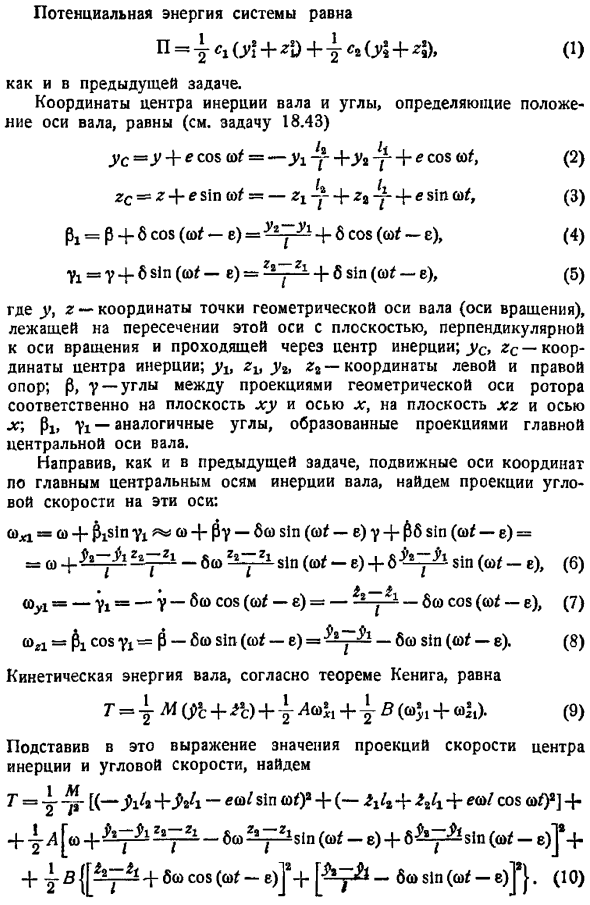
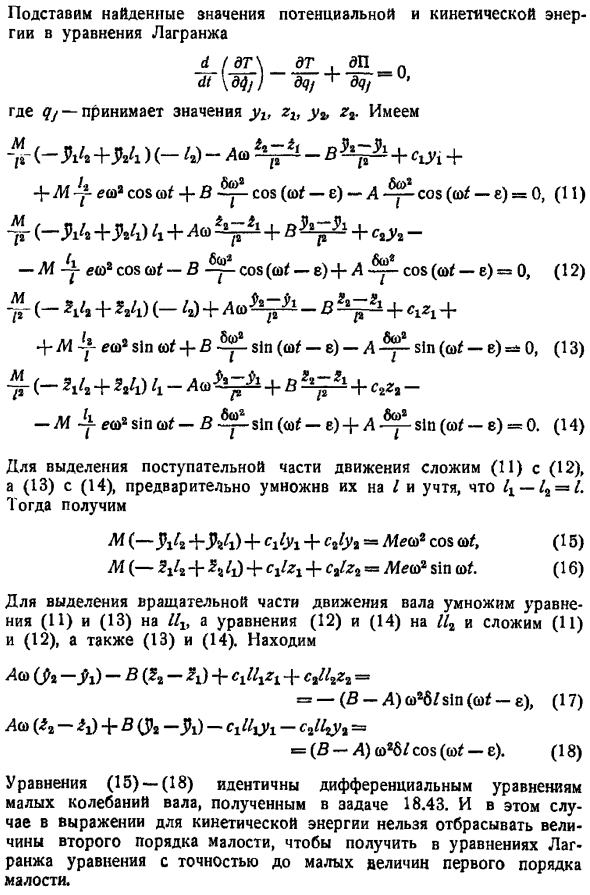

Применение уравнений Лагранжа в обобщенных координатах к составлению дифференциальных уравнений свободных и вынужденных колебаний вращающегося вала
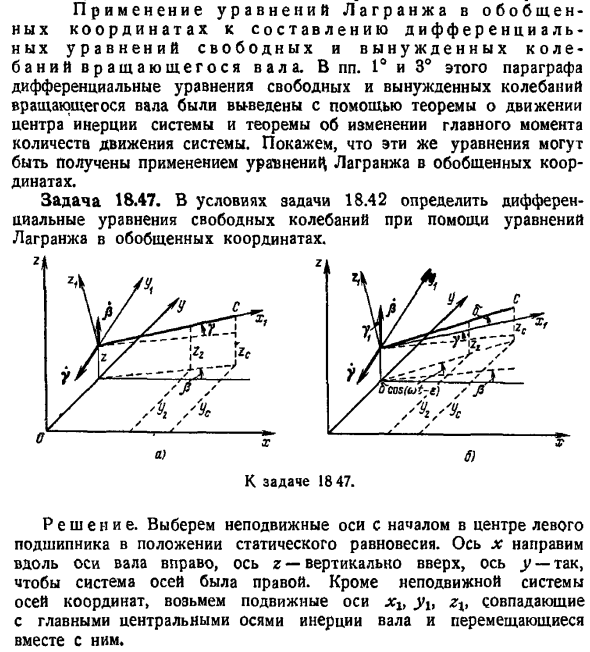
- В пунктах 1 и 3 в этом разделе дифференциальные уравнения свободных и вынужденных колебаний вращающегося вала были выведены с использованием теоремы о движении центра инерции системы и теоремы об изменении основного углового момента системы. Мы покажем, что, применяя уравнение Лагранжа с обобщенными координатами, мы получаем то же самое уравнение. Задача 18.47. В условиях задачи 18.42 уравнение Лагранжа обобщенных координат используется для определения дифференциального уравнения свободной вибрации. Вопрос в 1847. Решение. Выберите фиксированную ось, начиная с центра левого подшипника в положении статического равновесия. ось x расположена справа вдоль оси вала, ось z-слева, а ось y — справа.
Кроме неподвижной системы осей координат, возьмем движущуюся ось xit y , причем zit совпадает с главной инерционной осью вала и движется вместе с ней. П уС10 R — — CS zo, 1 Здесь, согласно условиям вопроса 18.41, вводится обозначение yb Zi, zt соответственно выбирают общие координаты координат левой и правой опоры, cb ct-коэффициент жесткости левой и правой опоры. Согласно теореме Кенига, кинетическая энергия вала равна сумме кинетической энергии центра инерции вала, вся масса системы сосредоточена в валу, а кинетическая энергия вала представляет собой относительное движение вокруг центра инерции. Р-4Т я е л и1 в, , ,.
Определить главный вектор количеств кулисного механизма, рассмотренного в задаче 262. Людмила Фирмаль
Где wx1, e 21-проекция угловой скорости вала на движущиеся координатные оси. Отметим, что угловая скорость вала состоит из 3-х элементов. w-угловая скорость вращения самого вала, направление вдоль оси XB, направление вдоль оси 0-z, проекция вдоль оси Y uh, находим Си 0sin ы я б г, 3 ол — г, 4 л pcosy. 5 Подставляя эти значения в уравнение кинетической энергии вала, замените усы Zc, 0 этими формулами см. вопрос 18.41 Л-л л С — — — А З.4 -, у — Мы получаем р-ж-д — — а.
В этом уравнении, если вы сохраните небольшое количество 2 7 14 К — Л, ЛУ — В- М 1 Подстановка значений потенциальной 1 и кинетической 7 энергии в уравнение Лагранжа ДТ ДП. ВР Л 3 dqj DQ в Куда Л, Zi, zt, найти дифференциальное уравнение движения вала Л 1 ЭМ-0, С — Л4 М 4 л ад,-о, 9 4 — в В4 −4 л-б 1 ад, — о, 10 4. М 4-Ла-41 г с АД, — О. 11 Чтобы разделить поступательные части движения, добавьте формулы 8 и 9, а также 10 и 11. 4-4 4 M число-число b1U1 s, 1 год −0, 12 Суи — см с Cflz О. 13 Чтобы разделить вращающиеся части движения вала, умножьте уравнение 8 и 10 на Hi, уравнение 9 и 11 на llt, снова на 8 и 9 и добавьте 10 и 11.А потом мы это выясним.
Полученное уравнение совпадает с дифференциальным уравнением колебаний малого вала, найденным в задаче 18.41 15-18. Особенностью составления дифференциальных уравнений движения с использованием уравнения Лагранжа с обобщенными координатами является необходимость сохранения малых квадратичных членов в выражении кинетической энергии.
- Это объясняется тем, что в уравнении Лагранжа кинетическая энергия выделяется малыми переменными обобщенными координатами и обобщенной скоростью. Задание 18.48.По условию задачи 18.43 мы создаем дифференциальное уравнение вынужденной вибрации вала, используя уравнение Лагранжа с обобщенными координатами. Решение. Рассмотрим вынужденную вибрацию вала, которая вызвана статическими и динамическими дисбалансами. Статический дисбаланс возникает, когда центр инерции смещается на небольшое расстояние е от оси вращения. Динамический дисбаланс определяется отклонением центральной оси основного вращения на небольшой угол 6 от оси вращения. н- , 3-я второй З 4, 1 Как и предыдущее задание.
Координаты центра инерции вала и угол, определяющий положение оси вала, равны см. задание 18.43 Йк Дж C0S — к г с COS о, 2 КЦ з Есин из -Цзы ЗТ-ж — е греха, 3 Пи П 6 Кос арт-с 6 в COS в-Е, 4 ух г грешить О -Е 1 я 6sin я Ф —э, 5 Где Y, Z-координаты точки геометрической оси вала оси вращения, на пересечении этой оси с плоскостью, перпендикулярной оси вращения и проходящей через центр инерции. усы, zc-координаты центра инерции. yy yy zt-координаты левой и правой опоры. p и y-углы между плоскостью X-Y и осью X, плоскостью X-Z и проекцией геометрической оси ротора на ось x соответственно. VI VI-аналогичный угол, образованный проекцией главной центральной оси вала.
Если бы человек, стоящий на гладкой горизонтальной плоскости, хотел подпрыгнуть, то он мог бы это совершить. Людмила Фирмаль
Как и в предыдущей задаче, если ориентировать координатные оси, движущиеся вдоль главной центральной оси инерции вала, то можно найти проекцию угловой скорости на эти оси. а Исин футов — М Ж — 6а грех В-С г 06 греха В-Е АА 0 1 Z1-6 0Z y 1 грех в-в 6 1- подоконник в-в, 6 айль — Йи — г-би в COS со — С — в COS в-с, 7 Я, потому что У1 — Би греха В-С — — 1-6 о грехе в-е. 8 Согласно теореме Кенига, кинетическая энергия вала равна р-г Я 0 я-у г-г, г б 51 г- Подставляя значения скорости центра инерции и проекции угловой скорости в этой формуле Т 2. А —Л4 м-съесть sinw 1 −2 2tlt поесть, потому что о Пи а о-6 о грех в-в 6 грех В-Е 2 в 6co cos at-e J 7 −6 0 sin co -e.
Подставим найденное значение потенциальной и кинетической энергии в уравнение Лагранжа о Л d4j йд, dqt Здесь qt-принимает значение yt, zb y g2.У нас есть — — M M — — -в Л М- им потому что искусство Б потому что в-с -значение COS п-е 0, 11 м Л4 4 8М с я- — M — ea2cosat-вcos CAF-в acos COF-е 0, 12 4 — 14 14 — аа я-б Mesha sin of В-sin at-в — грех of-в s 0, 13 4 — В1.4 4-АА Ч Б 1 с — M и с ним sin at-Bsin at-в Asin at-в 0. 14 Чтобы различить поступательные части движения, добавьте 11 к 12 и 13 к 14.Они были ранее умножены на I, принимая во внимание lL — 1. И — Я4 Л4 С11У1 mea2 cos at, 1 b М — 14 4 01 1 ctlzt Afeco2 sin at.
Для разделения вращающихся частей движения вала формулы 11 и 13 умножают на Z4, формулы 12 и 14 умножают на 11g, в дополнение к I и 12, В дополнение к 13 и 14.Выяснить АА ТВС-А — Б ст-ад cjl2z2 — Б-х о. 26 Син п-с, 17 АА ФА-ад Б J4 не-е — ая, ИСИ-ctlltyt Б — а о 6 со кроватка-е.
Смотрите также:
Предмет теоретическая механика

