Оглавление:



Применение теорий прочности в практических расчетах
- Применение теории прочности В реальных расчетах За столом. 13. приводится основная формула, полученная в предыдущем пункте. Эта таблица не содержит формул, связанных с теорией прочности Ю.I. Поскольку Ягна (см.§105) требует более обширной экспериментальной проверки. Основные проблемы, возникающие в
реальных расчетах, связаны с выбором конкретной теории прочности и соответствующих формул. Теория возможной энергии теория пластических материалов была выдвинута и подтверждена экспериментами. Есть отношение к хрупким материалам?В ^>
1, это хорошая идея, чтобы применить теорию Мора. Выбор критериев Людмила Фирмаль
прочности для анизотропных материалов должен осуществляться с учетом их механических свойств и особенностей условий работы. Следует также отметить, что в настоящее время применение существующей теории прочности достаточно обосновано экспериментально только для плоских напряженных состояний. В такого рода стрессовых условиях нужно встречаться чаще всего. П р и М Е Р1. На опасной части вала имеется изгибающий момент L4I=27500 кг-см, действующий на плоскость AB, крутящий момент L4kr=30000
кг-см(рис. 331). Выберите диаметр вала., Взятый на основе третьей и энергетической теории прочности [a]=500kpsm2. Максимальное касательное напряжение возникает во всех точках профиля сечения, а в точках А и в конца диаметра, совпадающего с рабочей поверхностью, максимальное нормальное напряжение-изгибающий момент.、 388T б л я с А13 Расчетная формула Название теории прочности для трехмерного напряженного состояния плоского
- напряженного состояния Первый Считанные секунды Третий. Энергия Теория Мора а) — ®1<[St] strasch=А1-Н(А2 4-4 — ®з)<[ст] В 1-a1ST8 +(ст1-З)2 4-* + (А2 — ®з)21<я strasch= * a3Est1 В 4 » стращ— ——- — ———-Н 4—в(^Х -^) А4-4г г х2<[а ] 1 — / ч В Рач-2 4 «П) 4″ -4~-1 (Х~У) 2+^2У х<н а Рейч=)/(а-СТУ)2 4» ^ 4г х<[а] 1 — / < штрасс-2 4 «1К~у (Х-У)2 4″Б?у Х<[®] В этом случае OU=0. Представлены А и Т через М К и мкр соответственно, и даны ему LSR16 Получаем при расчете третью теорию прочности (см. табл. Тринадцать.) Орк=/°2+^2=н , Откуда
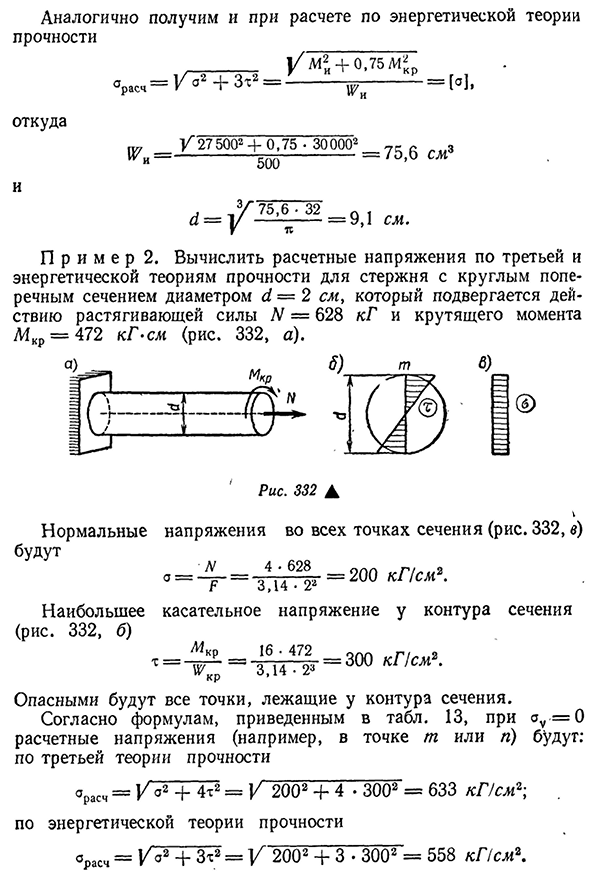
Таким образом, то же самое можно получить при расчете энергетической теории прочности °С= = я———— —- ————и=[о’ ] , Откуда ^_Gram 2 7 500″+0.75. 30000 » _7 5/6С л , И (/=1 / 7 5,6. 3 2=9 1 1 П р и М Е Р2. Расчет третьей и энергетической теории прочности для стержней с диаметром круглого сечения<1=2 см, с натяжением тяги N=628 кг и крутящим моментом MKR=472 кг 332, а). Рис 332А
Это будет нормально Напряжение во всех точках площади поперечного сечения(рис. 332, а) N_4-628 П~ ~ 3.14 * 22 =200kpcm*. Самый Людмила Фирмаль
крупный(рис. 332, Б) тангенциальное давление в контуре сечения 16 * 472 3.14 * 23 = 300kpcm?. На контурах опасного участка будут лежать все точки. По формуле, приведенной в таблице. 13, при AU=0 расчетное напряжение (например, в точке t или l) будет иметь вид:2002 4- 4 • 3002 =633 кг) в СМ\°C=/o2+Zt2=V2+3 согласно Энергетической теории прочности. 3002=558K, PSM.
Смотрите также:
| Понятие о новых теориях прочности | Основы расчета тонкостенных стержней открытого профиля основные понятия |
| Объединенная теория прочности | Свободное кручение тонкостенных стержней |

