Применение теории подобия для расчета поверхностного натяжения.

Применение теории подобия для расчета поверхностного натяжения.

Применение теории подобия для расчета поверхностного натяжения. Для представления температурной зависимости поверхностного натяжения можно использовать подобие изменения температуры исследуемой жидкости и соответственно выбранной стандартной жидкости (лучше всего, если жидкость аналогична). Карр и Волчинский [26]установили, что этот метод может быть использован для определения поверхностного натяжения при различных температурах, и показали зависимость по типу диаграммы Дюра. Для T1 и T1 поверхностное натяжение испытуемой жидкости и эталонной жидкости показывает одинаковое значение ab, а для T2 и T2 поверхностное натяжение равно ar, соответственно, его можно описать следующим образом. 7 * 2-L Г Г; = SOP51 (У1-26） В декартовой системе координат температура стандартной жидкости равна T [, Г2,Гз… Is на оси нанесена независимая переменная, температура Ti, Tg, Tg … y имеет такое же значение, как и следующее в поверхностном натяжении исследуемой жидкости. Для стандартных решений. На рисунке показана прямая линия.

Эмпирически экстраполяция показала, что такой показатель можно использовать в достаточно узком температурном диапазоне. Людмила Фирмаль

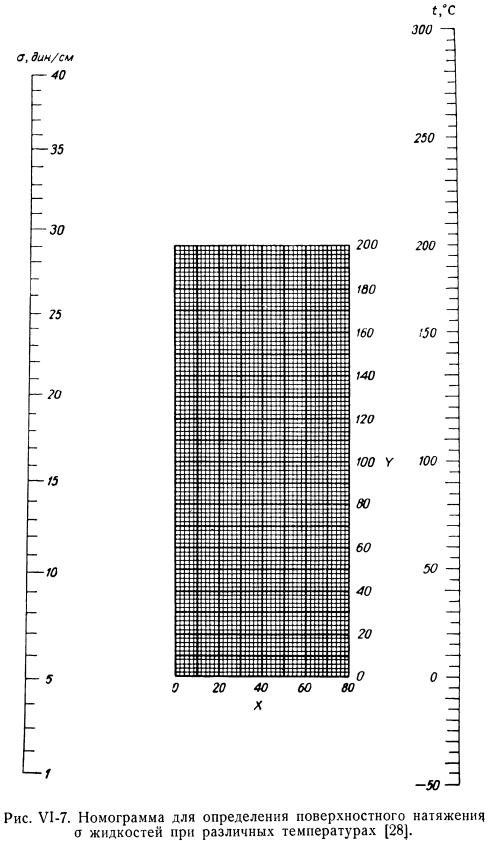
• Это связано с тем, что на больших интервалах прямая слегка изгибается, отклоняясь от прямой. Особенно большие отклонения наблюдаются вблизи критической температуры. Для редактирования рисунка достаточно иметь 2 значения поверхностного натяжения исследуемой жидкости:*при температуре Г и 02 при температуре Г2.Если известны критические температуры обеих жидкостей, то для температуры Ti достаточно только 1 CF, так как температура Гкр имеет поверхностное натяжение жидкости СР= 0. Более точные результаты можно получить с помощью графического метода, предложенного Otmer [27]. если o-поверхностное натяжение при температуре target целевой жидкости, o ’ поверхностное натяжение стандартной жидкости при температуре T \ Gkr, а Gkr-критическая температура целевой и стандартной жидкости, то: (VI-27） Рис, U1-7.Номограмма для измерения поверхностного натяжения жидкостей при различных температурах[28].

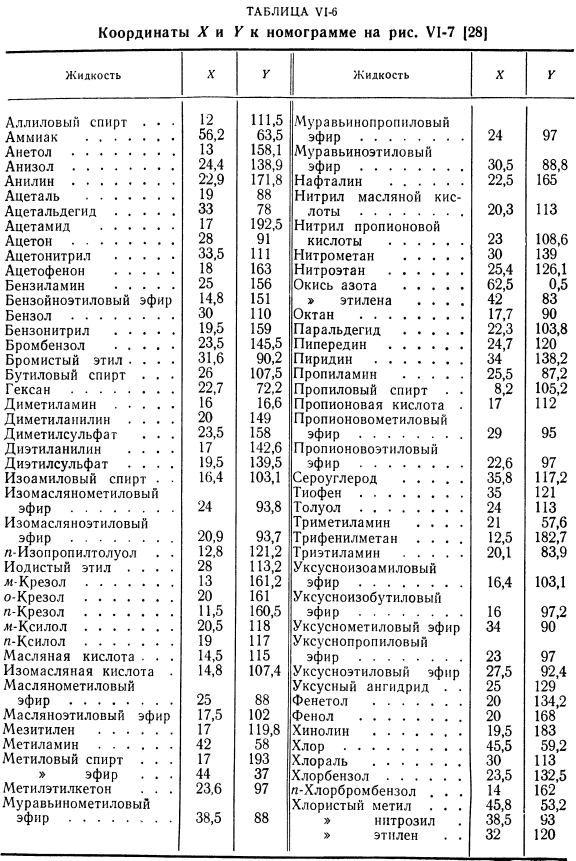
• Отмер нашел зависимость в T & it： 1 ^ 0 = / » 1 to ’+ C(Y1-28） Где rn и C-константы 2 рассматриваемых жидкостей. Если известны 01 и 02, то разница температур равна т т т’ * cr ’ 2-украинский 2 Вы можете определить значения поверхностного натяжения стандартных жидкостей 02 и 0, рассчитать значения констант px и C или нарисовать линейную диаграмму зависимостей от 1e до 1do’. Диаграмма Отмера превосходит предыдущую диаграмму и представляет собой температурную зависимость поверхностного натяжения в диапазоне температур, приближающемся к критическому Г|ф. В соответствии с уравнением (U1-28) была составлена точечная номограмма −100 жидкостей(рисунок U1-7).Вместо построения точек, соответствующих каждой жидкости на номограмме, добавьте таблицу координат этих точек (таблица U1-6) и примените сетку к номограмме для определения местоположения требуемых точек[28]. Они используют номограмму (рисунок U1-7) таким образом: согласно тому, что взято из таблицы. Когда Y1-6 преобразуется в координаты X и Y исследуемой жидкости, положение соответствующей точки в этой жидкости определяется на сетке номограммы.

Затем проведите прямую линию через найденные точки и точку на правой шкале, где определяется поверхностное натяжение, соответствующее температуре, пока она не пересечет левую шкалу с точкой, соответствующей требуемому поверхностному натяжению. Людмила Фирмаль

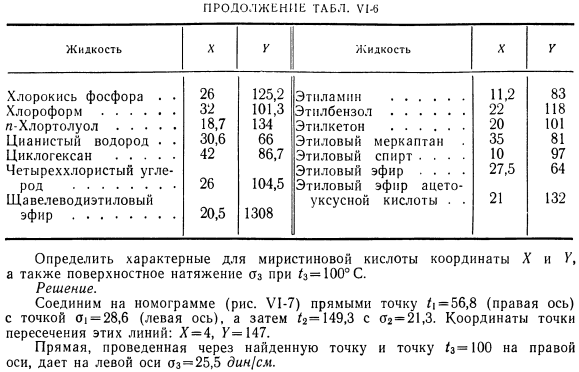
• Пример VI -! Определить поверхностное натяжение метилэтилкетона при 75°C Решение. Согласно таблице метилэтилкетон х = 23,6 U1-6; к = 97. Согласно номограмме (рисунок U1-7), A = * 18.（ Экспериментально установлено а = 17,8 дин/ см. Если значения поверхностного натяжения 01X известны для жидкостей 1X и 02, найдите координаты точек пересечения на сетке X-Y, соединив эти точки с осями I и о в номограмме (рис. Y1-7).Эти координаты можно использовать для определения поверхностного натяжения при любой температуре по номограмме. Пример U1-2.Экспериментально установлены следующие значения поверхностного натяжения миристиновой кислоты. 56.8 ° с,= 28.6 Дин / см / 2 = 149.3 ° cst2 = 21.3 Дин / см Таблица U1-6 Координаты X и Y для номограммы U1-7 (28） Продолжение табл. U1CH5. Определите характерные координаты X и V для миристиновой кислоты и поверхностное натяжение при f = 10°C o*. Решение. В номограмме(рисунок U1-7) соедините точки/|. = 56.8 (правая ось), точка 01 = 28.6 (левая ось), затем/ 2 = 149.3, 02 = 21.3.Координаты точек пересечения этих линий: X = 4, K = 147. Найденная точка и прямая линия через точку/ s = 100 на правой оси дают oz = 25,5 din/ cm на левой оси.

Смотрите также:

Решение задач по гидравлике

Возможно эти страницы вам будут полезны:

1. Расчет поверхностного натяжения смеси жидкостей.
2. Расчет поверхностного натяжения в зависимости от температуры и давления.
3. Зависимость поверхностного натяжения жидкости от различных физико-химических параметров.
4. Некоторые основные понятия кинетической теории газов.