Применение теоремы Кастильяно, теоремы Мора и способа Верещагина

Применение теоремы Кастильяно, теоремы Мора и способа Верещагина

• Применение теоремы Кастильяно, теоремы Мора и метода Верещагина. § Раскрытие статической неопределенности лучей, рассмотренных в § 136 и 137, также может быть сделано с помощью теоремы Кастильяно (§ 127). «Дополнительная» эталонная реакция(рис. 361, а) заменяет»дополнительную» неизвестную силу B,

действующую вместе с нагрузкой q, приданной главной статически определимой балке AB(рис. 361, б). Если вы дифференцируете силу на потенциальную энергию и вычислите отклонение/b, то/b будет равно нулю. уравнение(23.2) выглядит следующим образом: G’L7 —

» V -!’- o и<23< -> Остается вычислить м, установить пределы интеграла Людмила Фирмаль

и взять его: Как=+ ) 2 3-6). Поперечное сечение луча DV+x’j (23.5) принимает следующий вид: Дж[х-х Г X — б) Не менять КД Три. И так оно и есть. 5О—у Длина; уравнение?4_ = м- 8438 статически неопределенная роль[гл. XXIII Кроме того, он не отличается от описанных в методе сравнения деформаций. Раскрытие

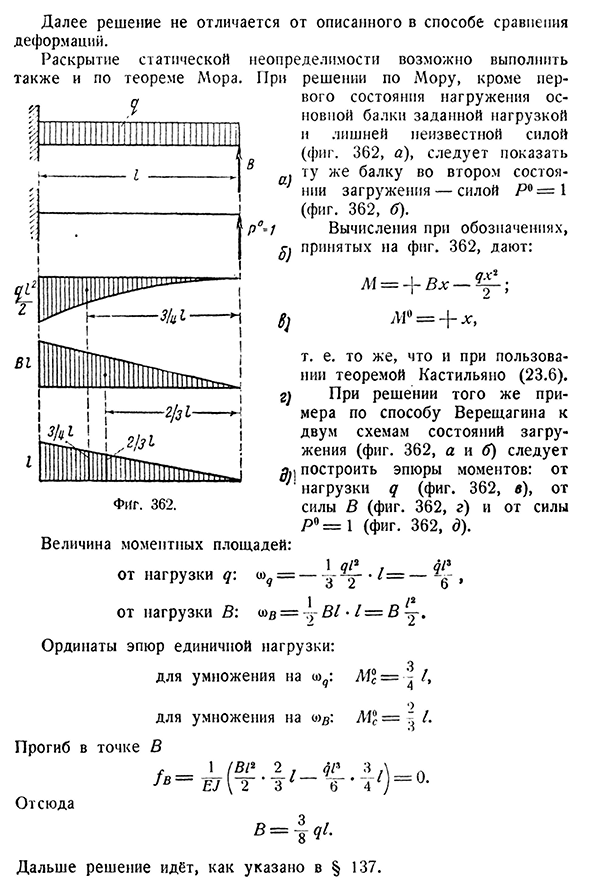
статической неопределенности возможно также с помощью теоремы Мора. За исключением Пер, в решении Мора- Фигура. 362. Между заданной нагрузкой и избыточной неизвестной силой и нагрузочным состоянием главной балки (рис. 362, а), во втором состоянии нагрузки должна отображаться та же балка-сила Р°=1(фиг. 362, б). Расчет

• обозначения, взятого на рисунке 362, дает X-L1°=C-X M^ — ^, Это то же самое, что использовать теорему Кастильяно(23.6). Этот же пример решается методом Верещагина и схемой двух состояний

нагружения(рис. 362, а и Б) необходимо построить график момента: нагрузки q(рис. 362, in), от силы In (рис. 362, г) от силы P°=1(фиг. 362, г). Размер крутящего момента в квадрате: нагрузка q: 1qP, qP^q— 2 * —

6 9 От нагрузки B:=Tf B L•I=B ордината единичной нагрузки график: Людмила Фирмаль

умножением на умножение Точка B отклонение / В qp6 И так оно и есть. Решение продолжается, как указано в§ 137.

Смотрите также:

• Примеры решения задач по сопромату

Общие понятия и метод расчёта	Выбор лишней неизвестной и основной системы
Способ сравнения деформаций	План решения статически неопределимой задачи.