Оглавление:




Применение симплексного метода для решения задач дробно-линейного программирования
- Применение симплекс-метода для решения проблем Дробное линейное программирование Линейность ограничений для линейных дробных задач Программирование и достижение экстремальных функций в экстремальных точках Область возможных решений проблемы позволяет Симплексный метод, чтобы решить это.
- Этого достаточно Измените только основные критерии оптимизации, разрешенные Решение проблемы. Чтобы вывести этот стандарт, Ниже. Заполните исходную симплексную таблицу обычным способом. Для этого введите две строки в верхней части таблицы вместо одной.
На верхней стороне числитель коэффициент Ζ \ (X) написан И коэффициент нижнего знаменателя. Людмила Фирмаль
Следовательно, следующее Вместо таблицы вводится 1 (t + 1) -я строка, две. второй -Линейный дробный знаменатель Ζ2 (Χ) этих строк Функциональная. Если линейный дробный функционал неоднороден, Добавляется к нулевому столбцу содержимое этих строк Освободите членов числителя и знаменателя соответственно.
Если линейный дробный функционал минимален, Построенная таблица преобразуется так же, как и линейная таблица Минимизируйте программирование, например, молекулы Ζι (Χ). так Достичь приемлемого базового решения для фракций Линейная задача. Чтобы вывести критерии оптимальности, Шаг s, получите следующую симплексную таблицу.
Он не содержит лучшего решения проблемы. значение Функционал задачи Z (s) на этом этапе получается как отношение Z (секунд) Числитель Ζψ и знаменатель Ζψ9, то есть Z (s) = — ^ -. Дай мне Xrk в настоящее время выбран в качестве разрешенного элемента в таблице (Вам нужно установить правила для этого места). Тогда новый (S + 1) -я таблица, числитель функции и знаменатель.
Форма Zis +,) = Ute? Mute-2- (Zlk-clk); Z2s + 1) = Zf- ± (Z2k-c2k), XRK XRK 119 Где Z \ k-c \ k и Z2k-C2k Функциональный знаменатель. тогда Ζ <* +! > = J ^. (11) Найти и преобразовать разницу между полученными значениями Функционально и до этого: 2 (с + D —Z & = s- * ,, (12) относительная влажность xi ~ *? {Z2k-C2k) + Zf (ZXk-clk) * lk 4s) (4s) — ^ (z2 ^ c2 *) j = 3 ~ Z *) (Z2k-C2k) + ZT (Zlk-Cik) *
- Обозначает следующие детерминанты. q _ \ Z \ k 6 \ k% Z \ | 22ft-C2kt Z2 I Этот определитель находится в числителе уравнения (12). В фракциях х Линейное программирование — минимум выбора Xrk χ. Симплекс отношения. Поэтому — <0. С (11) гк ΔΛ> 0 Z 0 Введенный вектор при максимизации функции В принципе, на самом деле соответствует наименьшему отрицательному.
Число Δ, очевидно, если Δ * = 0, то значение Функция следующего шага не меняется: Ζ ^ +! > = Z 0 (максимум). Пример 2. Найти оба экстремума функции (8) при ограничениях (9) — (10) Приведено к нормальной форме: 3αί-2hg— 10 Ζ = 2d, + * 2 + 3 ”* ϊ + * 2- * 4 = 5; (14) 5jf, -2dg2 + dgBП; (15) Xj> ©, i = 1, …, 5.
Искусственные ко второму главному ограничению (13) — (15) задачи. Людмила Фирмаль
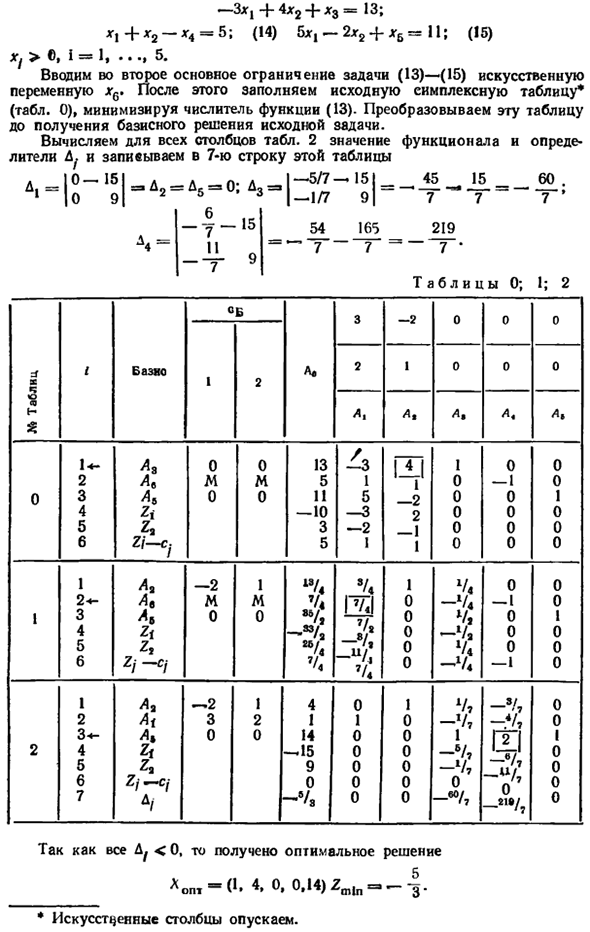
Переменная lg6. Затем заполните оригинальную таблицу мультиплекса * (Tab 0), уменьшите числитель функции (13). Преобразовать эту таблицу Чтобы получить базовое решение исходной задачи. Рассчитать для всех столбцов в таблице. Два значения функции и Определитель Δ Запишите в седьмую строку этой таблицы | —5/7 —.151> 45 15 60 -1/7 91 * 7 «* 7 7 ‘ ΔΙ = 0-15 , Δ2 = Δ5 = 0, Δ3 Δ4 = -τ-15 ϋ9 7 лет 54 J65 _ ^ 19
Поскольку все Δ ^ <0, оптимальное решение было получено. Aopt = (1, 4, 0, O.I4) Zm | n — §. * Искусственный столб опущен. Вы также можете определить максимальную функцию на основе таблицы 2 219 По этой причине мы вводим вектор A4 в базу, потому что минимум Δ, — = Δ4 => ~ — = -. Результаты расчета приведены в таблице. 3. Из всех неотрицательных Δ. Это включено в таблицу. 3 Этот Возможность оптимального решения Hopt = (5, 7, 0, 7, 0) maxZ = a β ~ 20 «
Смотрите также:
Примеры решения задач по математическому программированию
| Дробно-линейное программирование. Постановка задачи и свойства ее решения | Асимптотические решения задач дробно-линейного программирования |
| Графический метод решения задачи | Метод потенциалов |

