Оглавление:
Применение рядов в приближенных вычислениях
С помощью рядов можно приближенно вычислить значение функций, определенных интегралов, логарифмов, чисел, корней. Для вычисления приближенного значения функции в ее разложении в степенной ряд сохраняют первые к членов, а остальные члены отбрасывают. Чтобы получить погрешность найденного приближенного значения, надо оценить сумму отброшенных членов. Ошибка приближенного вычисления не должна превосходить абсолютную величину первого из отброшенных членов.
Задача №117.
Вычислить 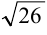 с точностью до 0,0001.
с точностью до 0,0001.
Решение:
Преобразуем данное выражение:
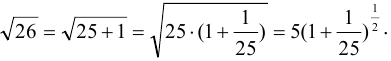
Для этого приближенного вычисления применим разложение функции 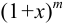 в ряд Маклорена, полагая
в ряд Маклорена, полагая 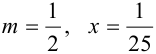 .
.
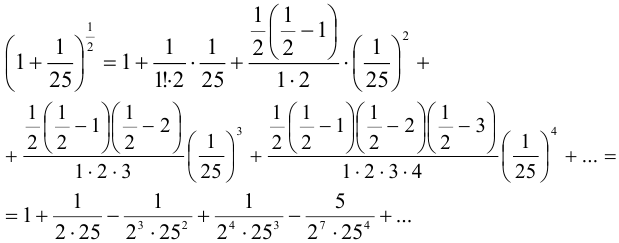
Полученный ряд является знакочередующимся рядом, для которого выполняются условия признака Лейбница.
Так как четвертый член ряда
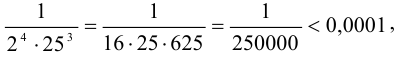
то отбросим его и следующие за ним члены ряда. Получим
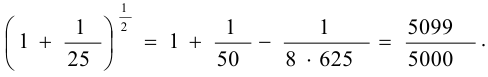
Следовательно, 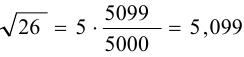 .
.
Задача №118.
Вычислить 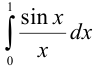 c точностью до 0,0001.
c точностью до 0,0001.
Решение:
Применить теорему Ньютона-Лейбница для неопределенного интеграла 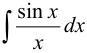 невозможно, т. к. этот интеграл не выражается в элементарных функциях. Воспользуемся разложением функции
невозможно, т. к. этот интеграл не выражается в элементарных функциях. Воспользуемся разложением функции 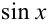 в ряд Маклорена:
в ряд Маклорена:
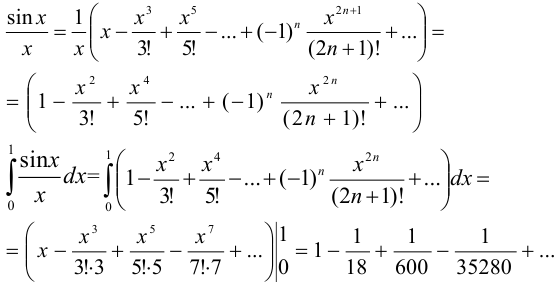
Так как 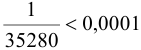 , то для вычисления интеграла с заданной точностью нужно взять три первых члена разложения:
, то для вычисления интеграла с заданной точностью нужно взять три первых члена разложения:
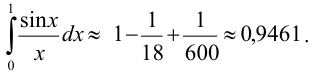
Задача №119.
С точностью до 0,001 вычислить 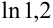 .
.
Решение:
Разложим функцию 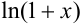 в ряд Маклорена:
в ряд Маклорена:
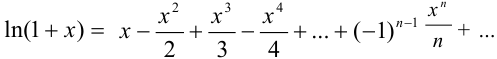
Положим 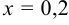 . Получим
. Получим
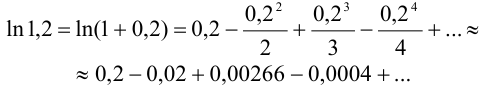
Так как 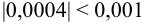 , то достаточно взять сумму трех первых членов:
, то достаточно взять сумму трех первых членов:
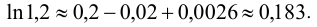
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Степенные ряды задачи с решением |
| Ряды Тейлора и Маклорена задача с решением |
| Операции над матрицами задачи с решением |
| Определители задачи с решением |

