Оглавление:




Применение полученных результатов к проверке прочности балок
- Полученные результаты были применены для испытания балки на прочность. Уравнение (13.9) решает задачу о величине и распределении нормального напряжения в поперечном сечении. В предположении, что его начало имеет сетчатый изгиб, часть, как ожидается, будет плоской. Исследования показали, что если Q не равно нулю, то сечения не только вращаются, но и несколько изгибаются под действием касательных напряжений. Однако эта
кривизна двух соседних участков такова, что она не изменяет установленного распределения деформации волокон, заключенных в этом участке, поэтому уравнение (13.9) может быть применено, если Q не равно нулю. Более к делу., Выше закона между ними На сегодняшний день правильнее всего применять эту формулу, когда поперечное сечение балки имеет ось симметрии, а внешние силы расположены в этой плоскости симметрии.
Нейтральная ось каждого участка, где подсчитывается G, проходит через центроид, перпендикулярный оси симметрии. Как использовать сто Людмила Фирмаль
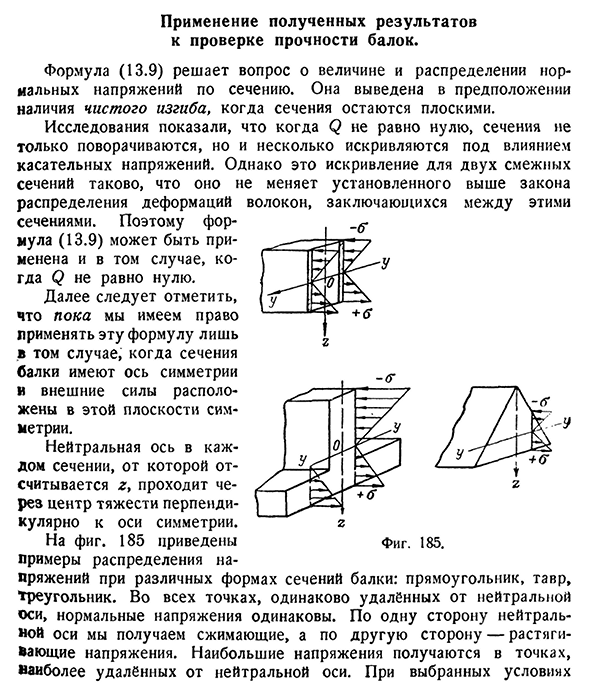
восемьдесят пять — <Г зет зет Фигура. Сто восемьдесят пять Примеры распределения напряжений в различных формах поперечного сечения балки: прямоугольник, t, треугольник. Во всех точках, равномерно расположенных от нейтральной оси, нормальное напряжение одинаково. С одной стороны нейтральной оси она сжимается, а с другой стороны получается растягивающее напряжение. Максимальное напряжение получается в самой дальней точке от нейтральной оси. Расчет 268 нормальных напряжений изгиба при выбранных условиях[глава XIII Что касается символов/и z, то формула (13.9) автоматически дает правильный знак для o,
за вычетом растягивающих и сжимающих напряжений. При положительном изгибающем моменте балка изгибается в выпуклой части, верхние волокна сжимаются (g<^0), а нижние волокна растягиваются. При отрицательном изгибающем моменте получается обратная картина. Поэтому при решении практических задач по подбору признаков нормального напряжения, если точки в разрезе задачи находятся в растянутой зоне, то, естественно, в этом случае формулу (13.9) следует заменить на абсолютные значения M и Z. Чтобы проверить прочность материала балки на нормальные напряжения, необходимо найти наиболее растягивающие
- и сжимающие участки. Для этого необходимо применить формулу (13.9) к опасному участку. Подставим его максимальное значение 7itah вместо M, а самое удаленное от нейтральной оси вместо z Тогда для самого высокого нормального напряжения получим следующую формулу ^тах — ^Т х2тах Как правило, эта формула преобразуется путем деления числителя и знаменателя на g t x. Значение — — — — — называется моментом сопротивления оси 2 Тер Поскольку J выражается в единицах длины четвертой степени, W измеряется в единицах длины третьей степени, например см\, (13.13) Куда? (13.14) Макс. В симметричном поперечном сечении относительно нейтральной оси, например, те прямоугольные, расстояние до крайнего удлинения и сжатые волокна одинаковы, такое
поперечное сечение является, таким образом, относительно оси Y высотой прямоугольника(фиг. 186, а), равный H.§ 79] проверьте интенсивность луча 269 Если поперечное сечение асимметрично относительно марки, то мы получаем два момента сопротивления. (Инжир. 186, Б): и другие для волокна: 1Г2 -=^ -. Теперь в Формуле «2» Так и должно быть (13.13). Введите: при расчете напряжения Wi-point A и 1g2-при расчете напряжения в точке B. Давайте перейдем к композиции- зет Около Фигура. Сто восемьдесят шесть Условия прочности на растяжение или сжатие. Это условие заключается в том, что максимум не превышает допустимого значения: По этой причине Фактическое напряжение Т’ ° — Надо (13.15)) (13.16) То есть момент сопротивления поперечного сечения балки,
необходимый для условий ее долговечности, должен быть не меньше максимального изгибающего момента, деленного на допустимое натяжение. Людмила Фирмаль
Поскольку W зависит от формы и размера поперечного сечения балки, то, выбрав форму (прямоугольник, Тор, двутавр), сопротивление поперечного сечения которой равно тому, что получено из Формулы (13.16), мы покажем ниже, как это фактически делается. Для прокатных профилей значения J и U7 указаны в таблице диапазонов (см. Приложение IX). При применении формул (13.15) и (13.16) необходимо различать два случая: В первом случае наиболее распространенным при изгибе является случай, когда материал одинаково устойчив к растяжению и сжатию, и в этом случае сопротивление обоим видам деформации.: [°Р]—[СИДЖЕЯ]—[°1- Затем, в симметричном сечении, не имеет значения, проверять ли прочность растянутых или сжатых волокон. Если асимметричное сечение в выражениях (13.15) и(13.16) вместо W, то необходимо
подставить значение W7! Или меньше 1G2, — и это будет относиться к более удаленному волокну.270 расчет момента инерции плоской фигуры[гл. XIV Второй случай имеет место, когда материал балки сопротивляется различным напряжениям и сжатию; тогда(см.§ 90 для получения дополнительной информации)вместо одного условия прочности мы можем видеть разницу.: — deg — =^YG>°C W= — (13.17) в зависимости от того, к чему материал более устойчив, к более крупному, [o]или[OJ], выберите его форму и размеры так, чтобы они соответствовали условиям прочности, а затем выберите его. Таким образом, формулы(13.15)и(13.17) дают возможность выяснить расчетное значение бак и требуемое значение резистивного момента балки в выбранном материале(допустимое напряжение). Чтобы
перейти от этого значения к размеру сечения, нужно научиться вычислять J и W для любой формы сечения. Как вычислить J и W показано в следующем абзаце. Что касается физического значения момента сопротивления, то оно ясно из Формулы (13.13). Таким образом, величина момента сопротивления зависит от влияния формы и размеров принятого сечения на интенсивность пучка при напряжении, не превышающем предел пропорциональности. Для напряжений, превышающих пределы пропорциональности материала, формулы (13.13) и(13.17) более не действительны.
Смотрите также:

