Оглавление:



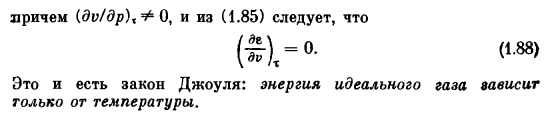

Применение первого начала к стационарному течению газа или жидкости. Процесс Джоуля — Томсона
- Состояние движущегося газа или жидкости определяется путем задания вектора скорости u, плотности p и температуры в каждой точке и в каждый момент времени. Давление выражается в плотности и температуре. Законы движения Ньютона дают 3 уравнения для этих функций. Уравнение неразрывности + див(ПУ)= 0(1.68) Получаем еще 1, 4-ю формулу, но есть 5 неизвестных.
уравнение дает закон сохранения энергии в энергетическом way. In в механике сплошной среды уравнение, представляющее закон сохранения энергии, является независимым уравнением. С другой стороны, в динамике точек (или точечных систем) выравнивание энергии является результатом уравнения движения Ньютона. Рассмотрим частный случай стационарного течения жидкости или газа, то есть состояния, которое не изменяется со временем в каждой точке пространства.
Второе начало термодинамики рассматривается не как ограничение на возможные процессы, а как ограничение на допустимый вид уравнений, описывающих реальные системы и процессы. Людмила Фирмаль
Теплопередача пренебрежимо мала, то есть предполагается, что процесс протекает адиабатически. Этот процесс не является квазистатическим (обратимым) процессом. Поскольку равновесие здесь нарушено, вывод§ 11 в данном случае неприменим. Поскольку движение является стационарным, линии течения жидкости не изменяются со временем.
Условием непрерывности установившегося потока является то, что масса жидкости, протекающей через любые 2 секции текущей трубки, равна same. So для любых 2 разделов o и ar、 Р | ШИ. = rgOgi、 Или путем ввода определенного объема. (1.69) (1-70) Напишите уравнение, представляющее первый принцип адиабатического процесса. Масса жидкой (или газообразной) энергии т — это сумма ее внутренней и кинетической энергии、 (1.71) Здесь e (o, t) — это определенная внутренняя энергия.
Работа на движении — это работа давления, оказываемого на поверхность массы m (мы считаем, что нет никакой гравитационной или другой внешней силы).Однако эта работа не равна pdV, потому что давление меняется от точки к точке жидкости (это важно при движении). Работа, проделанная массой m за время dt, будет равна сумме давлений сечений Oi и og, которые станут границей этой массы.
Эту задачу можно записать следующим образом. ДГ =(p₂a₂ih-п, о, U.) ДТ. (1.72) Для бесконечно малого элемента m、 тч-тч = дл-у%д..(1.73) Где dl-длина линии потока, которую занимает масса t. d (рай)_ d (Рой) dt dl ’ (1-74) Где d / dt-производная по времени («реальная производная») в точке, связанной с движущейся массой, А d / 01-производная по потоку (константа 4).Работая на время ДТ.
Итак, вы можете написать: (1.75) Подставляя (1.75) в уравнение(1.13). Это справедливо для любого процесса изоляции, учитывая(1.71)и (1.69)、 F (Е +u⁸’2) дл д(Пау)_» ДТ и ДТ Очевидно, m = adl / v; следовательно、 Д(Е + У ’/ 2)+(п / ас)д(Поу)= 0 (1.70) спасибо, d (au / v) — 0 так、 д (Пау)= dipvauM =(ас / в)д (ру)、 Д(Е +И2 / 2 + ФВ)= 0. Введем удельную энтальпию H = IJ / m \ тогда(1.79).
Это вдоль всей линии D (h + u!) / 2)= 0.Если поток медленный, то 2 мал, и когда жидкость течет, удельная энтальпия постоянна вдоль всего потока. ч = сопи (1.80) (1.76) (1.77) (1.78) (1.79) При выводе мы не учитывали работу внутренних сил трения (вязких), но пренебрегая 2, отбрасываем член той же степени, что и эта работа, так как работа силы трения в единицу времени пропорциональна мощности 2 скорости. Примените полученные результаты к эксперименту Джоуля-Томсона.
В рациональной термодинамике не обосновывают существование температуры на основе представлений о термическом равновесии; более того, такого рода доказательства рассматриваются как «порочные круги метафизики». Людмила Фирмаль
Целью джоулевского эксперимента было доказать, что энергия разреженного газа не зависит от его объема (закон Джоуля). как правило, можно использовать необратимость Адиабатическое расширение газов в а vacuum. In в этом случае работа не завершена, поэтому энергия остается постоянной. Если температура не изменяется из-за такого расширения, это означает, что энергия не зависит от объема, потому что(d£/ dt)1t + +(dE / dV) dV-0, а di = 0.
Однако на практике мы не можем сделать никаких выводов, поскольку теплоемкость сосуда, содержащего газ, больше по сравнению с теплоемкостью самого газа, а результаты экспериментов очень неточны. Поэтому для решения этой задачи мы использовали случай медленного теплоизоляционного течения Кева-Табана, который мы рассмотрели above. By вводя пористую пробку в трубку, по которой течет газ, реализуется медленный поток. Такой процесс называется процессом Джоуля-Томсона.
Экспериментально установлено следующее. Температура Tc и давление p p p p2 с обеих сторон заглушки. Кай указал, что определенные энтальпии происходят в этом курсе. предполагая, что д-р = Пи Поэтому в процессе Джоуля Томсона энтальпия L остается constant. So, можно сказать, что отношение Ei / Ep этого процесса равно производной (di / dp) H. учитывая dh / di-cp, из(1.83) Немецкая марка= (1.84>.
Газ, который можно считать идеальным, находится при-0, и поэтому это был эксперимент Ная. Отверстие = 0. (1.85> Это означает, что энергия идеального газа не зависит от его volume. In факт, для газа, который следует уравнению состояния крапейрона, pv = Ri (где D-Ссылка на выбранную единицу массы)、 ч = е(V, м)+ рv = Е(Н м)+ Дм (1.86> (1.87> Кроме того, от (dv / dp),+ 0 и (1.85) (£),- «•⁽⁽, — Это закон джоуля. Энергия идеального газа зависит только от температуры.
Смотрите также:

