Оглавление:








Применение метода зеркальных изображений
Применение метода зеркального отображения. Метод зеркального отображения широко используется для расчета магнитного поля, создаваемого линейным током, протекающим вблизи стального слитка.
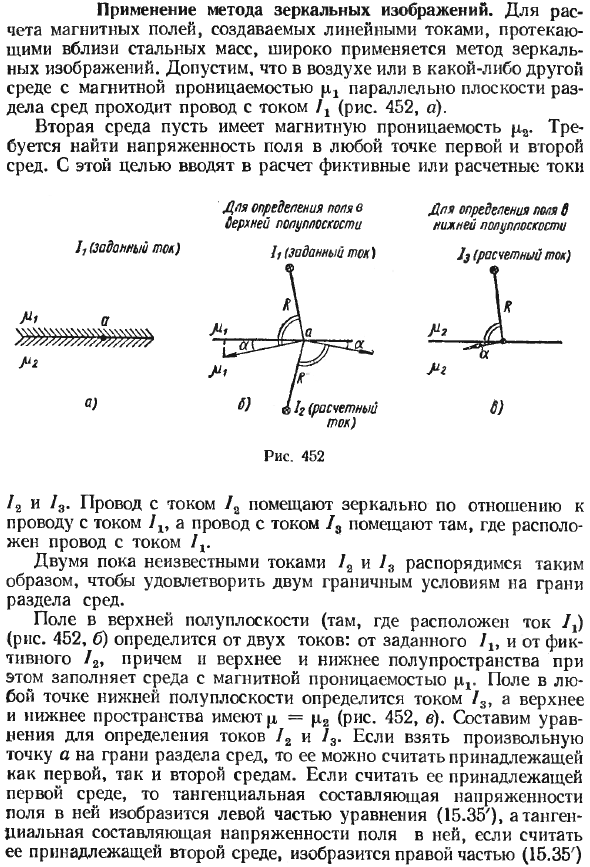
- Предположим, что проводящий провод течет параллельно границе раздела среды в воздухе или другой среде с проницаемостью (рис. 452, а). Вам необходимо придать второй среде проницаемость и
найти напряженность магнитного поля в любой точке на первом и втором носителе. Людмила Фирмаль
По этой причине фиктивные токи или номинальные токи / 2 и / 3 вводятся в расчет. Ток / провод помещается как зеркало относительно провода тока / х, а провод тока / 3 размещается там, где находится провод тока / d.
Обработайте два неизвестных тока / a и FAC для удовлетворения двух граничных условий границы раздела между средами. Магнитное поле в верхней полуплоскости (рис. 452, б) определяется двумя токами: в этом случае из заданного мнимого / 2 верхнее и нижнее полупространства заполнены проницаемостью ,
- При current / 3 верхнее и нижнее пространство имеют вид p = p2 (рис. 452, c). Настройте уравнение для определения токов / 2 и / 3. Взяв произвольную точку a на границе раздела между средами, можно предположить, что она принадлежит первой. Так что это вторая среда.
Предполагая, что оно принадлежит первому окружению, t о тангенциальная составляющая напряженности электрического поля в нем представлена в левой части уравнения (15.35 ‘), а
тангенциальная составляющая напряженности электрического поля в нем принадлежит второй среде Людмила Фирмаль
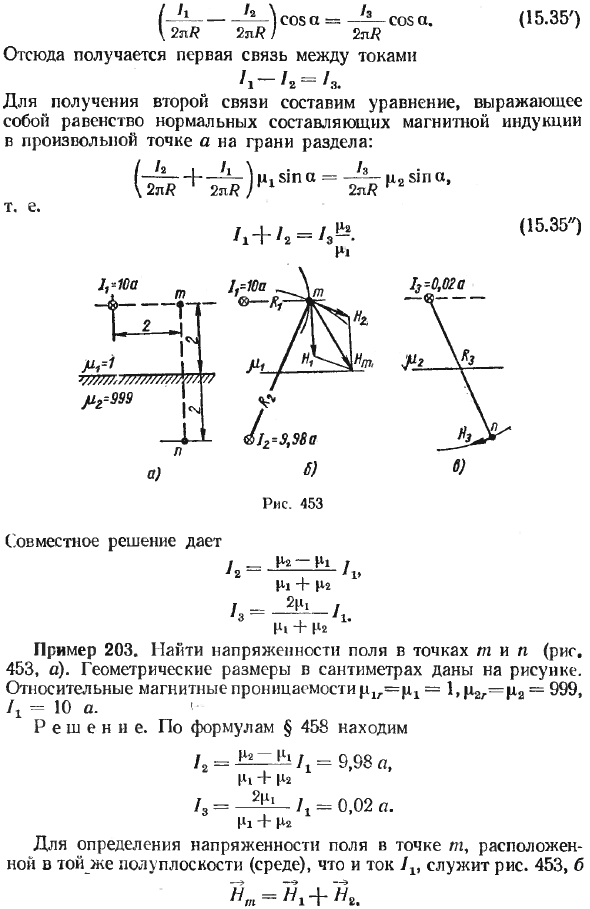
Представлено справа (15.35 ‘) (-? L_Vos a = ——- cos a. (15.35’) \ 2nR ZnR / 2l /? Отсюда ток A ~ / 2 = / s Получите первое соотношение: u2sina, \ 2l /? 2l /? L 2l / ?? / 1 + 4 = (15,35’3 дает решение / -Na-Hi f l2; * y Hi + Р2 /-2Н1I.У1 Pi + Щ Пример 203. Найти напряженность поля в точках m и n (рис. 453, а).
На рисунке показаны геометрические размеры в сантиметрах: относительная проницаемость plr = Pi = l, | n2z = | i2 = 999, = 10 a. <• Решение. 4 = n в соответствии с §458, = 998 H1 Hi + H2 4 = /, = 0,02 A. P1 4-Pa. Чтобы определить напряженность поля в точке m в той же полуплоскости (среде), что и ток / х, рис. 453, b I, = I + ‘4
Закон полного тока N = = ^ — = — = 79,5 (a / l), n2 = -A- = 1 2l /?! 2l.0.02 2l /? 2 9 93 == 35 2 l 4.48. M Nt ~ 101 a / m, путем нахождения 10’2 графически Напряженность поля точки n (рис. 453, в) ne = i = A = A® = 0,0715 (а / л). 3 н 2л /? 3 2л. 4,48. Ю-2 ‘рис. 454, а — ток Качественно показывает фотографию провода
B магнитной индукции, когда проточный провод течет в воздухе, параллельном поверхности стального листа. На рисунках 454 и b показана фотография провода B, когда проволока, по которой течет ток, проходит. Проходит через узкий канал в стальной пластине, параллельной поверхности пластины.
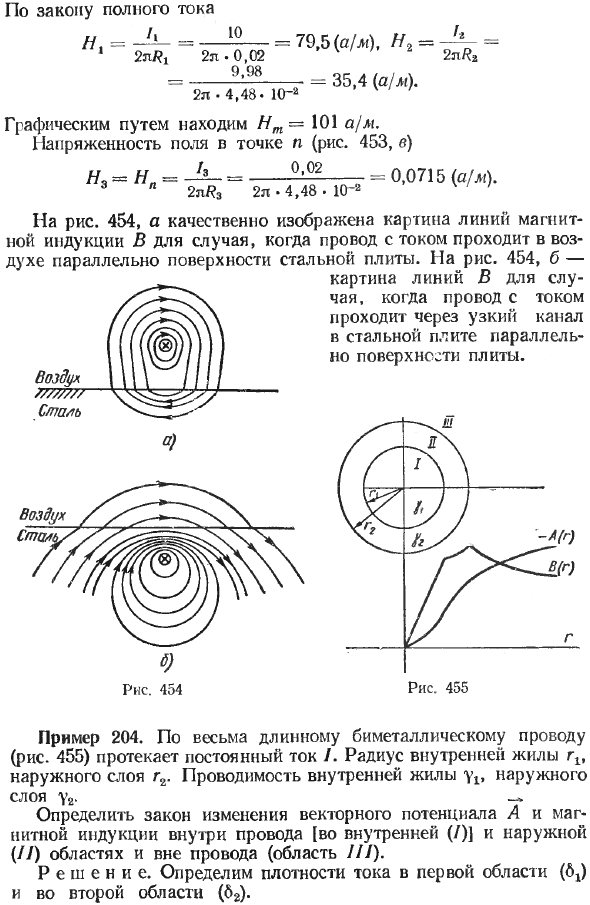
Пример 204. Постоянный ток протекает через очень длинный биметаллический провод (Рис. 455). Радиус rlt внутреннего сердечника внешнего слоя g2. Внутренний сердечник y1e внешнего слоя y2 — *
Определить закон изменения векторного потенциала A и магнитной индукции в [/] и наружной (II) областях внутри проволоки и вне области (область III) P ehne.Первая область (6 Определите плотность тока J и второй области (q2), потому что Eu = Ew —.
С другой стороны, Yi Y2, поэтому 61 = А 6r = dx ^. η] 4-3 3 (г ^ Я- ??) Y * Yi При расширении уравнения в цилиндрической системе координат в этой задаче A имеется только одна компонента A = 2 ° Ar-2qA, D) И этот компонент зависит только от r: -p2d2 в первой области -p2d2 во второй области, O rr \ dr в третьей области) удваивается на r
Интеграл есть ^ = — Г1 + с11г, r + c2> A / = -e ^ + cz111r + c4. L // 7 = C61n + S. Термины C и In r не должны существовать. Поскольку A не может принимать бесконечно большое значение при r = 0, CL = 0. Векторный потенциал определяется с точностью до постоянной.
Кроме того, проволока ось А-0. Составьте уравнение, чтобы определить оставшиеся четыре константы из граничных условий. 1. Если r == rx Aj = Ajp, то M * 1 = • ^ M- + c3lnrl + C4. 4 4 2. Когда r = r2, An = Ar, то есть _ + C3 In r2 + C4 = C5 In r2 + C6. 4 1 al, 1 alp 1 1 lt * u dr p2 dr faJ ^ 2 ^ * 1 2 2 года! 4.
Для r-r2 тангенциальные составляющие напряженности поля должны быть равны. 2 C2G 2 C, = ^ (6, -60. _ 6Ig? -R?) + M U5-2 Нз »С, = -Н> 6 <1_ _] _Н? M. _ sz In g ;; C6 = -4- 4 4 4 4-C31n2 + C4 -C6! Pl2. Рис. 455. Одна кривая показывает схему изменения — A — f (r), а другая кривая показывает схему изменения B = f (r) при — = — и p. = Та 3,5 == П2 = Из. l -> ->
Пример 205. Используя формулу す る = () А (и данные из примера 204, найдите магнитный поток, проникающий в биметаллическую проволоку примера 204 на длине -1 м. (15.26) Φ = ■) Adi. Разделите путь интеграции на четыре раздела. Первый раздел из точки / в точку 2 (см. Рисунок 456, а).
Второй раздел от пункта 2 до пункта 3. Третий — от 3 до 4, а четвертый — от точки 4 до точки /. Следовательно, 2 _ 3 _ 4 _ 1 ([‘A d / = j A 111 + f dl «г. (A dl -J-f A di. I 5’ .I 4 2 JA dl равно нулю, поэтому второе А в четвертом разделе угол между A и dl равен ± 90 ° и cos 90 ° = 0, поэтому A dl также равен нулю. JAdl не равен нулю только в третьем разделе
В третьем разделе A = — ^ l — \ — c3 \ nr2 + Ct, а угол между A и di равен 180 ° (потому что 180 ° = -1), поэтому 4Ф = f A dl * ^ -А-1.з r = GG «Ха Пример 206. Используя структуру рис. 450, магнитопроводность воздушного зазора между полюсом машины постоянного тока и якорем на единицу длины (1 м) якоря Определите nn 2 и m -11; — = 0,9 согласно рисунку 450.
Формула (15.29): 1,256-10 ^ -1-0,9-11 = 6 207 на основе 23 т 10_n 207. Цилиндрическая проводимость Схема поля участка кабельной линии длиной 1 м 2-проводной кабельной линии с броней показана на рисунке 456, b (er = 2.5), поле, и согласно § 452 линии электрического поля соответствуют эквипотенциалу магнитного поля, число трубок электрического поля составляет m = 10.5-2 = 21.
Ячейки в трубе Число n = 10 (5 от проволоки к броне, 5 от брони к проволоке). Отношение равно ^ 1. Число магнитных трубок равно m = 10, а количество ячеек в трубке равно n = 21. Рассчитайте емкость на 1 м (/ = 1 м) длины кабеля, используя уравнение (15.31): C = 46. 10-! 2 (f)> 10
По определению индуктивность L представляет собой отношение магнитного потока L к току L В этой задаче есть только один виток (прямая проводка и обратная проводка), поэтому магнитная индукция φ равна магнитному потоку, равному между проводами (индуктивность, обусловленная магнитной индукцией в корпусе провода, мала и не учитывается)
Согласно закону полного тока, ток I можно заменить на (| H dl Вдоль замкнутой цепи, окружающей провод, тогда f // dl представляет падение магнитного напряжения Um вдоль этой цепи, поэтому L = ® = ^ = Cu / J Индуктивность L равна магнитной проводимости Гм.
Чтобы определить последнее, используйте уравнение (15.29) * Gm = L = J— = 6 ■ IO «7 (r»). Пример 208. Найти разницу в скалярном магнитном потенциале (линейный ток / = магнитное напряжение между точками A и B в магнитном поле 10a) (рис. 457). , UmAB = J I dl = J /? Dl + JH dTt
A находится вдоль пути AmC вдоль пути CnB, и в этом разделе угол между H и dl pa находится вдоль пути SpB вены 90e, поэтому это не путь AmC J II dl-0. itAv = — ^ = 2,5 А. Пример 209. В воздухе было создано однородное магнитное поле // // 0-240 А / м. Ферромагнитный шар помещался в это магнитное поле, и его относительная проницаемость составляла t = 20.
Найти наведение мяча. Решено и е. Используйте сходство между статическими и не вихревыми полями. В уравнении (13.69) замените Eq на Ho, e на p и получите Ht = n. — = 240 = 32,7 а / м. «Eun, индукция с 2 + 20 шариками = 20.32.7. 1.256. 10» b = 8.21. При расчете L с использованием формулы 10-4 тонны G Гм количество ячеек в силовой трубке должно быть получено в замкнутом цикле.
Пример 210. Постоянный ток течет по трубе с внутренним диаметром rg и внешним диаметром r2 (рис. 458). Выведите формулу для определения напряженности электрического поля H внутренней полости трубы, корпуса трубы и наружной части трубы. Решения. Найти напряженность поля в одной из этих областей по закону полного тока.
Если вы нарисуете круг с радиусом r r2, напряженность электрического поля уменьшается по гиперболическому закону 2lg. График H-f (r) показан на рисунке. 458. * ## Закон Био-Сеира-Лапласа известен в области физики.
Согласно этому закону при отсутствии ферромагнитной среды обрезание линейного провода d /, через которое протекает ток / ток, создает магнитную индукцию дБ в точке, удаленной от элемента тока R, определенного как дБ = (15.36) 4l R2 v ‘->
Это единичный вектор, выведенный из d / до точки, где определяется магнитная индукция (Рисунок 459). Вывод результата в этой точке = [1 ^ 1 • (15.37) 4l J point2 7 l Уравнение (15.37) выполняет интегрирование по всей длине замкнутого контура, включая ток.
В уравнении (15.36), если ток 1 вводится как постоянное число 1 в векторное произведение, Idl заменяется на bdVt, а dV — это элемент объема проводника с плотностью тока b, тогда dB = —1 -‘- -b- (15.38) 4l Y2 » и B- | (15.39) 4l JЯ2 » В уравнении (15.39) интегрирование выполняется в соответствии с «текущим занятым» объемом.
Формула (15.38) описана в литературе под названием закона Ампера. На практике уравнения (15.37) — (15.39) применяются, когда интегрирование может быть выполнено очень легко. Два простых примера применения формулы (15.37) показаны на стр. 649. В заключение обратим внимание на два момента.
1. Структура уравнений (15.36) и (15.38) в некоторой степени аналогична структуре уравнения напряженности поля для точечно-заряженного электрического поля, полученного из закона Кулона в 382.
2. Закон полного тока удобно сравнивать с законом Биосавалла Лапласа. Оба эти закона могут определять магнитную индукцию, вызванную током. Однако закон полного тока применяется только к замкнутым цепям, содержащим ток, а закон Био — Савара — Лапласа применяется не только к замкнутым цепям, содержащим ток, но также и к сегментам проводника (элементам тока) со стоками.
В этом смысле закон Био — Саварда — Лапласа является более универсальным. Пример 211. Используйте уравнение (15.37) для определения магнитной индукции в точке / n, создаваемой сегментом линейного провода e current / (Рисунок 460). Точка m удалена от провода на расстояние />.
Решения. Угол между dl и R обозначен как. По геометрическим причинам есть R = -, / = —детга. sin a Следовательно, dl-bda-t sin2 a I \ dl Yao] I = d / • 1 • sin a, dB = sin a da. 4nZ> B = ■ f sin a da = — (cos a. -Cos a2). 4nfr J 4nh V 1 2 ‘»1
Вектор B направлен на считыватель. Если провод бесконечно длинный, ar = 0, a.2 = 180 °, cos a * -cosa2 = 2 и B = — ^ 1— Это согласуется с результатом, полученным по закону полного тока, Пример 212. Вывод уравнения, определяющего напряженность магнитного поля на оси кругового витка тока 1 (рис. 461), радиус поворота равен
Решение: выберите текущий элемент Idl, напряженность поля d / 7, созданную этим элементом в точке b на оси поворота на расстоянии r от плоскости поворота / (a? W | 4l (A2 + z2)), интенсивность dH ‘перпендикулярна dl, а ток 7 dl в той же точке b от противоположного элемента становится напряжением dl /’.
Абсолютные значения dH ‘и dH «одинаковы , Геометрическая сумма dH ‘и d / G дает вектор вдоль тока малой петли: dl = a da, 2 πla sip p da 4l (a-p z2) Γda = -. 4l (a2- | -r2) z2) ‘/ «J 2 (a2 4-z2) 7’
Смотрите также:
| Графическое построение картины поля и определение по ней магнитного сопротивления. | Определение переменного электромагнитного поля. |
| Магнитное экранирование. | Первое уравнение Максвелла. |

