Применение метода конформного отображения

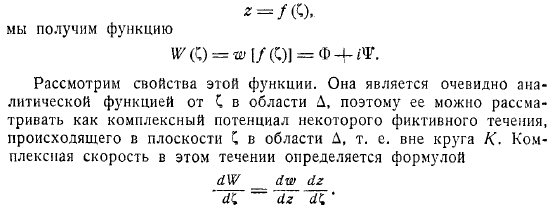
Применение метода конформного отображения

Применение метода конформного отображения. Полученное выше общее решение задачи об обтекании поступательным потоком кругового цилиндра позволяет решить задачу об обтекании произвольного контура, если только известно конформное отображение внешности гидромеханики этого контура на внешность круга. Обозначим через область плоскости, расположенную вне рассматриваемого контура и содержащую внутри себя бесконечно удаленную точку плоскости.

Введем в рассмотрение формулу Кутта-Жуковского вспомогательную плоскость значим через окружность с центром в начале координат этой плоскости и через радиус этой окружности. Область плоскости, расположенную вне и содержащую бесконечно удаленную точку, обозначим через. Между областями можно установить взаимно однозначное конформное соответствие при помощи однозначных аналитических функций.

• Это соответствие устанавливается единственным образом, если потребовать, чтобы точки соответствовали друг другу и чтобы значение производной голоморфна в области, за исключением точки, в которой она имеет, очевидно, полюс первого порядка. Поэтому эта функция должна разлагаться в ряд Лорана следующего вида, согласно принятому выше условию о значении производной в бесконечно удаленной точке.

Предыдущий ряд сходится в любой конечной точке области. Если в плоскости провести окружность с центром в начале координат, целиком содержащую внутри себя контур, то в области, расположенной вне, функция тоже должна разлагаться в ряд Лорана. Этот ряд является, очевидно, обращением предыдущего ряда, и его коэффициенты легко могут быть выражены через. Например. Заметим, что радиус круга можно брать произвольно, и тогда определится значение действительной постоянной к.

Можно было бы принять; можно, наоборот, принять, что, и тогда значение полностью определится. Рассмотрим теперь задачу о безотрывном обтекании контура потенциальным потоком, имеющим на бесконечности скорость. Соответствующий комплексный потенциал обозначим, как обычно, через. Подставив сюда вместо его выражение через мы получим функцию. Рассмотрим свойства этой функции.

Она является очевидно аналитической функцией от в области, поэтому ее можно рассматривать как комплексный потенциал некоторого фиктивного течения, происходящего в плоскости в области, т. е. вне круга. Комплексная скорость в этом течении определяется формулой. В бесконечно удаленной точке мы имеем следовательно. Значит, в бесконечно удаленных частях плоскости мы имеем поступательный поток со скоростью.

С другой стороны, очевидно, что в соответствующих точках плоскостей имеют место равенства, так как на контуре функция имеет постоянное значение (условие обтекания), то значит на контуре функция будет иметь тоже постоянное значение, и, следовательно, контур является эффективной линией тока для течения, определяемого комплексным потенциалом Из сказанного ясно, что определяет обтекание круга потенциальным потоком, имеющим на бесконечности скорость.

Конформное отображение — непрерывное отображение, сохраняющее углы между кривыми, а значит и форму бесконечно малых фигур. Людмила Фирмаль

Эта задача была решена в; следовательно, должна иметь следующий вид. Подставляя сюда, мы получаем комплексный потенциал дающий общее решение задачи об обтекании контура. В решение вошла произвольная постоянная, определяющая циркуляцию по контуру. Для случая гладкой  реакции на контур, не имеющего угловых точек, значение циркуляции должно быть задано; как раз такой случай мы имеем в задаче обтекания круга. Профили крыльев, употребляющихся в авиации, имеют обычно острую кромку.

• В этом случае при произвольно выбранном значении циркуляции скорость в острой кромке получится бесконечной и только при одном совершенно определенном значении скорость в острой кромке останется конечной. Н. Е. Жуковский предложил так именно и определять значение циркуляции, чтобы скорость в острой кромке оставалась конечной. Физический смысл этой гипотезы Н. Е. Жуковского можно пояснить следующим образом: пусть контур, находившийся сначала в покое, начинает двигаться поступательно и равномерно в жидкости, покоящейся на бесконечности.

По теореме Томсона, циркуляция скорости по жидкому контуру, охватывающему контур, должна сохранять свое значение с течением времени и, следовательно, должна все время иметь значение, равное нулю. Вообще говоря, нулевое значение циркуляции не удовлетворяет условию конечности скорости в острой кромке контура, так что скорость вблизи точки будет иметь очень большое значение. Заметим теперь, что действительные жидкости всегда обладают вязкостью.

Как мы увидим во второй части курса, даже при малой вязкости жидкости нельзя пренебрегать действием сил вязкости вблизи стенок, в данном случае вблизи контура. В результате действия этих сил в тонком, прилегающем к контуру слое жидкости образуются вихри, которые срываются затем с контура внутрь жидкости. Если теперь рассмотреть два контура и и обозначь через — циркуляцию по контуру, то ясно, что циркуляция охватывающему контур, будет равна, так как циркуляция по всему контуру как мы видели выше, равна нулю (этот контур целиком лежит внутри жидкости, где действием малых сил вязкости мы можем пренебречь).

Процесс срыва вихрей с преобладанием вихрей одного знака будет продолжаться до тех пор, пока циркуляция не достигнет такого значения, при котором скорость в задней кромке контура будет конечной. Сорвавшиеся с контура вихри при движении контура останутся далеко позади него. Таким образом объясняется установление определенного значения циркуляции при поступательном равномерном движении контура. Очевидно, то же самое, рассуждение применимо и к задаче об обтекании контура. Определим теперь, исходя из гипотезы Жуковского, значение циркуляции для контура, имеющего острую кромку.

Пусть точке соответствует в плоскости точка круга. Если касательные к контуру в точке образуют угол, то в точке преобразование перестанет быть конформным; так как угол между двумя касательными к кругу в точке равен внешний угол между касательными к контуру в точке равен. То с точностью до малых высшего порядка преобразование области в область вблизи точки дается формулой; отсюда ясно, что при в точке. По правилу дифференцирования сложных функций.

В точке А первый множитель справа остается ограниченным по модулю, а второй, как только что установлено, обращается в нуль, следовательно. Иными словами, точка должна быть одной из критических точек фиктивного течения в плоскости. Подставив в равенство значение и приравняв результат нулю, без труда найдем. Воспользовавшись, наконец, тригонометрическим представлением получим.

Итак, для контура с острой кромкой циркуляция определяется по формуле. Как видим, вся трудность в решении задачи о безотрывном обтекании контура поступательным потоком сводится к отысканию конформного отображения области на внешность круга. Прежде чем переходить к примерам, вернемся к вопросу о вычислении сил, действующих на контур.

Простейший пример — преобразования подобия, ими исчерпываются все конформные отображения всего евклидова пространства на себя. Людмила Фирмаль