Оглавление:




Применение метода конечных разностей
- Графическое решение уравнения Фурье плоской пластины с использованием метода конечных разностей O было предложено Биндером E. Он стал универсальным способом изучения проблем нестационарной теплопроводности и других связанных с ней процессов. Многочисленные применения этого метода описаны в литературе. 4). Основы этого метода представлены при рассмотрении задачи 8. Задача 8. Тело ограничено одной стороной. С одной стороны, в ограниченном теле устанавливается распределение температуры, которое является временем/ = 0, зависит только от 1 координаты x и определяется уравнением 0 = P (x). Поверхность тела находится в контакте с пространством нулевой температуры.
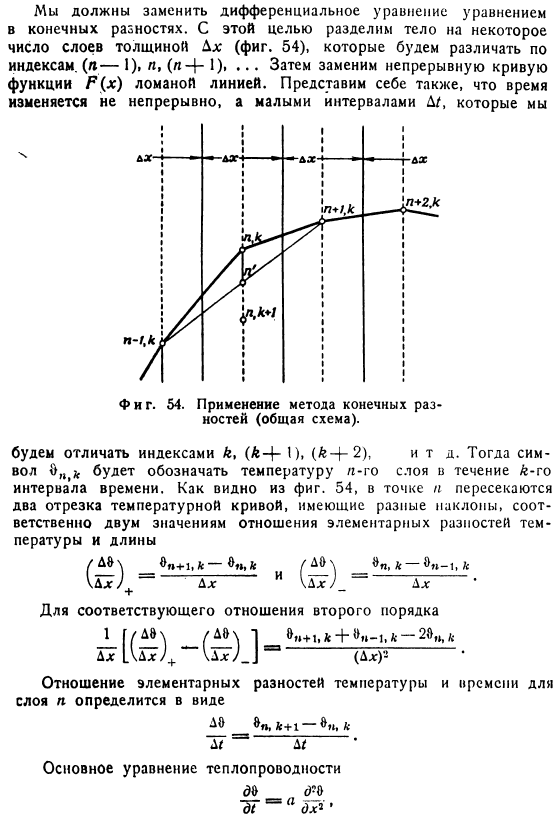
Известны физические константы и коэффициенты теплоотдачи тела. Этот процесс характеризуется различиями Уравнение Граничные условия 3-го вида: similar. It необходимо заменить дифференциальные уравнения уравнениями конечного типа difference. To сделайте это, разделите тело на несколько слоев толщиной Дх (рисунок 54), индекс(—1)、、、(4 4-0″•••затем замените непрерывную кривую функции P (x) пунктирной линией. В коротком интервале D/, а не в непрерывном、 Различают по индексам k, (LC-I), (k-^-2) и др., а символ 0k обозначает температуру n-го слоя в N-й раз interval. As это видно из рисунка.
В практике в большинстве случаев тепло передается жидкости от твердой поверхности, с которой соприкасается жидкость, и пар образуется в виде пузырей, которые возникают и растут на греющей поверхности, затем, достигнув определенного размера, отделяются и поднимаются через жидкость. Людмила Фирмаль
Пункт l 2 сегмента температурной кривой пересекаются, каждый с различными градиентами, до 2 значений отношения основной разности между температурой и длиной Для соответствующего отношения 2 Отношение основной разности между температурой и временем слоя l определяется как: Основное тепловое уравнение Формат, записанный в конечных разностях, является: Или Выражение в круглых скобках с правой стороны показана на Рис. 4.
Точки в интервале между n ’и (n, г), n’ находятся на линии, соединяющей точки (n-|-1, A) и (n-1, k).Различия слева Уравнение представляет собой изменение температуры за период времени в точке (l, k).Таким образом, эта разница пропорциональна расстоянию от, согласно последней формуле (Л, К) от L ’ Если я могу, коэффициент пропорциональности равен 2a Если вы преобразуете этот коэффициент в единицу, то точка[l, (/ e + 1)] перейдет непосредственно в точку l’, и графическая техника, описанная ниже, будет намного simpler. It это возможно.
Достигается благодаря свободе выбора расстояния Dx и D/.Очевидно, что необходимо придерживаться таких правил для выбора временного интервала, соответствующего отношениям. Например, если рассматривать бетонную стену толщиной 40 см (а = 0,002 м2 / час), то по точности графической техники извлекается около 8 слоев, в результате чего х = 0,05 м. Тогда о временном интервале Решение той или иной задачи обычно начинается с определения значения Dx, что удобно для графического построения. Затем создайте начальное распределение температуры в виде ломаной линии 0. 1, 2, 3. 。 Кроме того, по выбранным значениям Dx и коэффициента термодиффузии a вычисляют значение временного интервала D/.
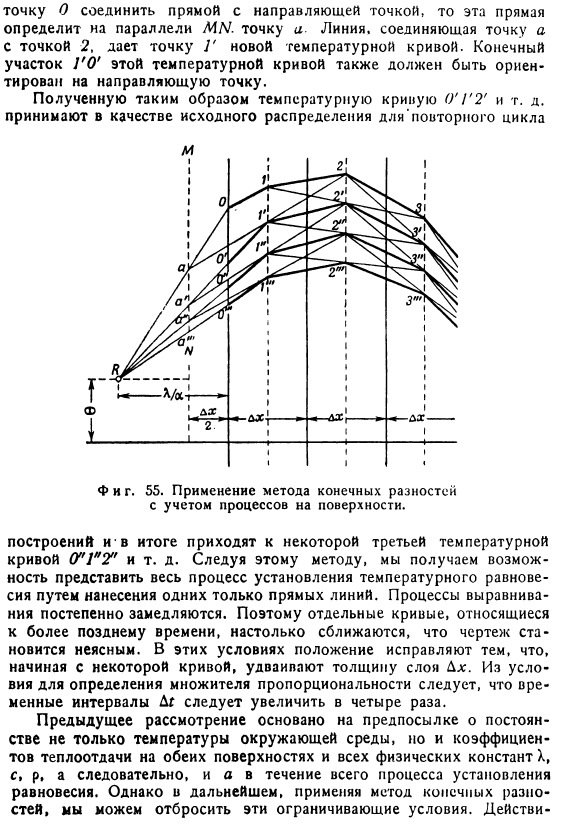
Затем соедините точку/с точкой 3 и получите точку 2’.Соедините точки 2 и 4 и получите точку 3!это не. Чтобы определить точки O ’ и Γ, необходимо также рассмотреть состояние поверхности. Конец температурной кривой в соответствии с выводом, показанным на стр. 28 (отсюда、 В этом случае направление GO’) должно быть направлено к заданной направляющей точке K, где ордината фиксируется температурой окружающей среды, а абсцисса фиксируется касательной$ = X / a. Итак, сначала найдите направляющую точку K, а затем нарисуйте линию MM с расстоянием Dx / 2, параллельным поверхности. Если В связи с этим Э.
- Шмидт называет предложенный метод «срезанием углов». Когда вы соединяете прямую линию с направляющей точкой с помощью точки 0, эта линия определяет параллельную линию. Точка а линия, соединяющая точку 2 с точкой а, дает точку G новой температурной кривой. Последняя часть этой температурной кривой, GO, также должна быть направлена в направляющую точку. Полученная температурная кривая O’g 2 ′ и др. принимается в качестве начального распределения цикла. Тоже фигура. 55.Применение разностного метода с учетом поверхностного процесса. Наконец, определенная 3-я температурная кривая (Г1 «Т и т.
Равновесие, рисуя только прямые линии. Процесс выравнивания замедляется slowly. So, отдельные кривые, которые позже связаны, являются Нарисуйте как можно ближе, чтобы рисунок был размытым. В этих условиях ситуация корректируется тем, что, начиная с определенной кривой, толщина слоя Dx оказывается в 2 раза выше. Из условий определения факторов Пропорционально этому временной интервал Dg должен быть увеличен в 4 раза. Предыдущие соображения основаны на предположении, что коэффициент теплопередачи обеих поверхностей и всех физических констант постоянен, а также температура окружающей среды. X, c, p, и таким образом в течение всего процесса установления равновесия.
Так как трудно с уверенностью предсказать, когда будет происходить капельная конденсация, то рекомендуется расчеты всегда производить по формулам для пленочной конденсации. Людмила Фирмаль
Однако в будущем вы можете использовать разностное исчисление, чтобы отбросить эти ограничения. Фактически, из-за того, что, независимо от всех предыдущих кривых, каждая промежуточная температурная кривая служит отправной точкой для новой структуры.、 Расчет с использованием положения направляющей точки после изменения. При изменении температуры окружающей среды или при изменении значений K и a направляющая точка/? Он фиксируется и начинает двигаться по кривой.
Если физическая константа X, сир, зависит от местоположения, вы можете рассмотреть это с помощью соответствующего варианта масштаба Аналогично, если физическая постоянная изменяется с температурой, то точка, полученная резанием, равна Угол не реагирует непосредственно на новую температуру. Преимущество рассматриваемого метода заключается именно в том, что с его помощью можно преодолеть возникшие трудности Исследование этой задачи(то есть задачи о температурном поле среды, в которой изменяются физические константы).Из-за нелинейности дифференциального уравнения、 Существует аналитическое решение.
Если есть источник тепла или источник тепла, необходимо сделать графическое изменение значения изменения температуры. Производительность источника. Э. Шмидт распространил метод конечных разностей на проблему цилиндра, сферы, стержня переменного сечения и даже теплопроводности. Задачи теплопередачи в движущейся среде и аналогичные процессы диффузии и переноса импульса.
Заслуживает внимания монография 1) Верона сравнивает численные методы со многими графическими методами решения задач с теплопроводностью стационарных и нестационарных, а также несколькими методами Электрическая аналогия. Применение релаксационного метода к случаю нестационарной теплопроводности описано на стр.
Смотрите также:
| Тело, ограниченное с одной стороны (полуограниченное пространство) | Метод электрической аналогии |
| Комбинированные краевые задачи | Стационарное температурное поле без источников тепла |

