Оглавление:
Применение дифференциала к приближенным вычислениям
Как уже известно, приращение 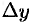 функции
функции  в точке
в точке  можно представить в виде
можно представить в виде 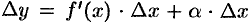 , где
, где 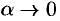 при
при 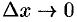 , или
, или 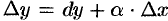 . Отбрасывая бесконечно малую
. Отбрасывая бесконечно малую 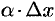 более высокого порядка, чем
более высокого порядка, чем 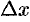 , получаем приближенное равенство
, получаем приближенное равенство

причем это равенство тем точнее, чем меньше 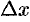 .
.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.
Пример №24.3.
Найти приближенное значение приращения функции  при
при 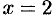 и
и 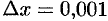 .
.
Решение:
Применяем формулу (24.3): 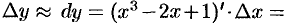
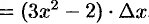 .
.
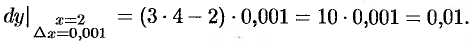
Итак, 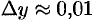 .
.
Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем 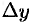 :
:
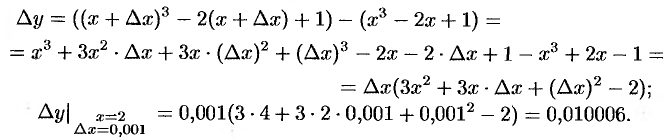
Абсолютная погрешность приближения равна
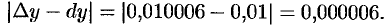
Подставляя в равенство (24.3) значения 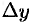 и
и 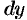 , получим
, получим
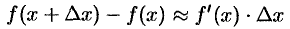
или
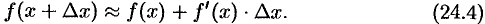
Формула (24.4) используется для вычислений приближенных, значений функций.
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Производные высших порядков неявно заданной функции |
| Производные высших порядков от функций, заданных параметрически |
| Дифференциалы высших порядков |
| Теоремы о дифференцируемых функциях |

