Оглавление:

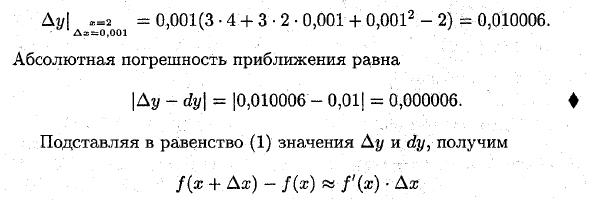

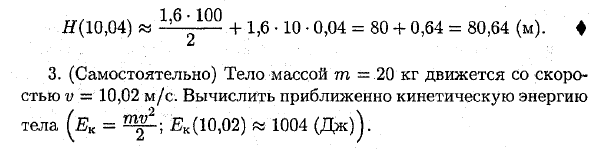
Применение дифференциала к приближенным вычислениям
- Применение различий для приблизительных расчетов Как известно, приращение A y функции y-f (x) в точке x может быть выражено в виде A y = f ′ (x) • Ax + oc • D.m. Где Ax 0 равен 0, A y = dy- \ a-ah. Отказ от бесконечно меньшего a • Ax выше, чем Ax, дает приближенное уравнение. Ay «DY, (1) Кроме того, это уравнение более точное, а Ax меньше. Это уравнение позволяет рассчитать приблизительный прирост дифференцируемой функции с высокой точностью.
Пример: если x = 2 и Ax = 0.001, найдите приблизительное значение функции y = x2-2x + 1 приращение. ♦ Применить формулу (1). «Dy =.» (X3-2x + 1); ■ Ax = = (3×2-2) • Ax. dy \ «= 2 = (3 • 4–2) • 0,001 = 10 • 0,001 = 0,01. 1 D «= 0,001 Итак, «0,01. Давайте посмотрим, какие ошибки допускаются путем вычисления разности функции, а не приращения. Для этого найдите A y. y = ((x + Ax) 3-2 (x + Ax) + 1) — (x3-2x + 1) = x3 + 3×2 Ax + 3x • (Ax) 2 + (Ax) 3-2x-2 • Дата + 1-x3 + 2x-1 = = Dx (3×2 + 3x • Ax + (Ax) 2-2);
Уравнение (1) широко используется в вычислительной практике, потому что различия обычно намного проще, чем приращения функций. Людмила Фирмаль
Ах | * -2 = 0,001 (3 • 4 + 3 • 2 • 0,001 + 0,0012-2) = 0,010006 J = 0,001 Абсолютная погрешность аппроксимации Ay-dy \ = | 0,010006-0,01 | = 0,000006. ♦ Подстановка значений A y и dy в уравнение (1) дает f (x + Yes:) — f (x) «f ‘(x) ■ Ax. или f (x + yes;) ”f (x) + f \ x) • Да: (2) Уравнение (2) используется для расчета приблизительного значения функции. Пример: 1. Рассчитать около arctgl, 05. ♦ Рассмотрим функции} {x) = arctg. Из уравнения (2): arctg (z + J) «arctga: -f (arctg w) ‘• J, Это arctg (x + Yes;) «arctan x — ^^.
| Дифференциал функции и его геометрический смысл | Дифференциалы высших порядков |
| Основные теоремы о дифференциалах. Таблица дифференциалов | Теорема Ролля |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- После: + Yes. = 1,05, затем x = 1 и Yes: = 0,05: arctg 1,05 «arctan 1 + = j -h 0,025» 0,810. ♦ 1 т 1 4 Можно показать, что абсолютная ошибка в уравнении (2) не превышает 4 ^ — (J) 2. Где М — максимальное значение \ f «(x) \ сегмент [a ;; a; + да;]. 2. По какому пути тело движется при свободном падении луны через 10,04 секунды от начала падения? Уравнение свободного падения тела H = 9 * ^, 9 «= 1,6 м / с2. ♦ Вам нужно найти # (10.04).
Используйте формулу аппроксимации (AN “dH) H (t + At) H H (t) + H ‘(t) • Ат. При t = 10 с и At = s dt = 0,04 с, # ‘(0 =№ (10,04) «1,601Q ° + 1,6 • 10 • 0,04 = 80 -f 0,64 = 80,64 (м) ♦ подветренный 3. (Независимо) объект с массой t = 20 кг движется со скоростью v = 10,02 м / с.
Рассчитать приблизительную кинетическую энергию Тело (£ k = EK (10, 02) «1004 (Дж)). Людмила Фирмаль

