Оглавление:




Приложения уравнений Лагранжа. Интеграл энергии
- Если связь не зависит от времени и выполняется без трения, то теорема о кинетической энергии выражается следующим уравнением: dT = 2 Xdx + Y + Z dz. Это включает в себя основную работу только данного forces. В частности, если эти силы имеют силовую функцию U, то существует энергетический Интеграл T = U h. эти теоремы могут быть легко восстановлены на основе уравнения Лагранжа. Если соединение не зависит от времени, вы всегда можете выбрать параметр QV q2. дь. Убедитесь, что координаты x, y и Z, выраженные этими параметрами, явно не содержат время t. В этих условиях вы можете: Xdx г ды я з ДЗ = = Qldql + Q2dq2 + … Qkdqk.
Таким образом, уравнение кинетической энергии описывается следующим образом: 7 = Ци + щ х + + мг Это равенство, являющееся результатом принципа Д Аламбера, должно быть также результатом уравнения Лагранжа. Это можно легко проверить следующим образом: в рассматриваемом случае T является однородным многочленом 2 го порядка относительно q .Значение+основано на уравнении Лагранжа Мы получаем + + Qkq K = ДТ 7 ДТ dqt q dqk По теореме однородной функции Эйлера выражение ДТ П стальтд ДТ Ци ТТ + ИТ ТТ + + Як ТТ Он равен 2T. с другой стороны, поскольку T явно не включает ДТ ДТ N. dT c. dT, нет. dt Ди ИГ + Так… Я, Г 2Т ДТ ДТ + + Qk4k Т Ай = Ди Это уравнение кинетической энергии.
Предыдущая формула показывает, что ось качания и ось подвеса взаимно обратимы, так что если подвесить тело за ось качания, то прежняя ось подвеса станет теперь осью качания. Людмила Фирмаль
Первый Интеграл этого уравнения получается каждый раз, когда является совершенной производной функции U от ГВ. ..дь. И затем… ДТ = ду, Т = П Н. Как мы видели, если данная сила имеет силовую функцию, то такой результат получается 1 У1 1 одно предприятие Поскольку энергетический Интеграл является результатом уравнения Лагранжа, интегрирование последнего можно упростить, заменив наиболее сложные уравнения Лагранжа энергетическим интегралом.
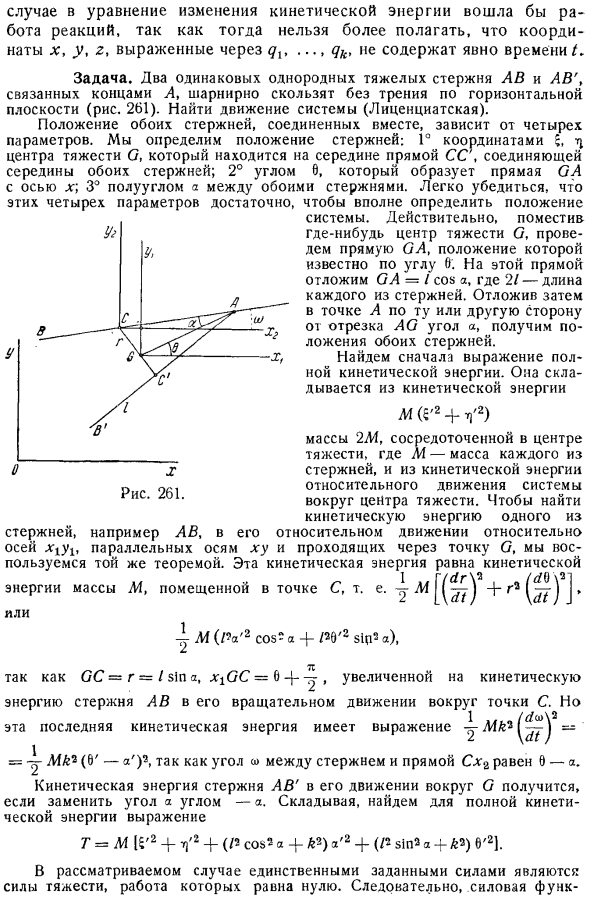
Вышеприведенные расчеты были проведены в рамках субстантивного предположения о том, что взаимосвязь не зависит от времени. Если вы этого не сделаете, qlt …. реакция входит в уравнение изменения кинетической энергии, так как координаты x, y, 2, выраженные в qk, уже нельзя считать явно не содержащими времени. Проблема.2 одинаковых однородных тяжелых стержня AB и AB , Соединенных концами A, скользят закрученными без трения вдоль горизонтальной плоскости рис.261.Проверьте работу системы лицензионной. Положение обоих стержней, соединенных вместе, зависит от 4 параметров. Определите положение стержня. G координаты, Q центроид G.
Это находится в середине прямой линии CC , которая соединяет середину обоих стержней. Угол 2 0.форма осью X и линией га. Полуширина 3 и между обоими rods. It легко видеть, что этих 4 параметров достаточно. Полностью определите местоположение system. In фактически, расположите центр тяжести G где нибудь и нарисуйте прямую линию GA, где положение известно из угла 0.В этой строке поместите GA = cosa. Где 21 длина каждого стержня. Затем поместите угол a в точке A с обеих сторон сегмента AG, чтобы получить положение обоих стержней. Во первых, найти выражение полной кинетики energy.
- Состоит из кинетической энергии 2а 2 + г 2 Масса M, которая находится в точке C, то есть M Масса 2М, концентрируется на центре тяжести. Где M масса каждого стержня, а от кинетической энергии зависит относительное движение системы вокруг центра тяжести. Как найти кинетическую энергию Стержень, например AB, использует ту же теорему в своем относительном движении относительно оси xtylt через точку G, параллельную оси xy. Эта кинетическая энергия равна кинетической энергии. Или Е + Ах M Za 2 COS a 4 30 2 Sin3 a РФО 2 GC = r = sin a, x GC = 6 4 увеличивается на кинетическую энергию стержня AB при вращательном движении вокруг точки C. Но эта последняя кинетическая энергия имеет формулу Mk.
Так как угол w между стержнем и прямой Cx2 равен 0 A. Если заменить угол a на угол a, то кинетическая энергия стержня AB оказывается в движении вокруг G. найти формулу для полной кинетической энергии, складывая T = U U U 2 + j2 2 5 cos3 a 4 n 2 + p sina a 4 L3 0 21. В этом случае заданной силой является только сила притяжения, работа которой является zero. As в результате силовая функция равна 7 = 0, а правая часть уравнения Лагранжа равна нулю. Если вы напишете уравнение координат S, то получите 0.Оттуда 6 = 0.Аналогично из уравнения m Если = v 0.As в результате движение центроида является простым и равномерным, что непосредственно следует из теоремы движения центроида.
Если совершенно свободное твердое тело, на которое не действуют никакие внешние силы, начнет вращаться вокруг одной из главных центральных осей инерции, то оно будет продолжать вращаться вокруг этой оси и притом равномерно. Людмила Фирмаль
Об уравнении ДТ ДД ДД ДД Вид = 0, поэтому и 7 не содержит 0.Прямая dT 7 Интеграл,= const или З грех я 0 = С. Я вы также можете написать уравнение для a, но оно становится очень сложным. Замените это на энергетический Интеграл. Здесь T = const, то есть COS g 4 a 2 + sin a 4 A O 2 = , U Потому что 6 и Y константы. Левая сторона представляет собой сумму квадратов, поэтому вы можете написать положительные константы в природе на правой стороне. Уравнение I показывает, что знак 0 не изменяется, поэтому линия GA всегда вращается вокруг G в одном и том же направлении. direction. In кроме того, угловая скорость этого движения обязательно равна C Между.
Подставьте значение 0, найденное из выражения I В Формуле II это выглядит так: d 2 Z COS а4 sin a +0 =Л sin а4 О. Левая сторона всегда положительна, поэтому правая сторона должна быть положительной. Если C A отрицательно, то a, очевидно, может принимать любое значение, и стержень, в зависимости от того, является ли q положительным или отрицательным, уходит или идет вместе d 0 или D = mf. Если С Л положительно, то эта разница равна i4 sin .Где где является реальным constant.
Факт, C A No всегда меньше, чем A .Это означает, что в первый момент, когда a = q0, величина a реальна, и поэтому A sin q0 C A .Поэтому условия, при которых угол q должен быть соблюден, следующие: грех д грех a изменяется между 3 mc p, так что движение каждого стержня относительно GA колеблется. Наконец, если С Л = 0, q может принимать любое значение, но если q стремится к mc или нулю, то t стремится к бесконечности.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

