Оглавление:
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
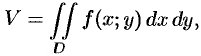
где 
— уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4)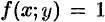 
, то цилиндрическое тело «превратится» в прямой цилиндр с высотой 
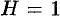. Объем такого цилиндра, как известно, численно равен площади 
основания 
. Получаем формулу для вычисления площади области :
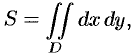
или, в полярных координатах,
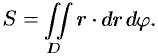
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки с переменной плотностью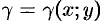 
находится по формуле
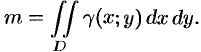
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры относительно осей 
и 
(см. п. 41.6) могут быть вычислены по формулам
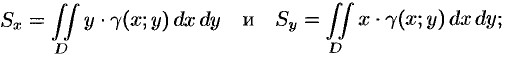
а координаты центра масс фигуры — по формулам
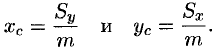
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы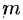 
относительно оси 
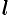называется произведение массы 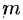на квадрат расстояния 
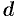точки до оси, т. е. 
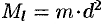. Моменты инерции плоской фигуры относительно осей и 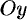могут быть вычислены по формулам:
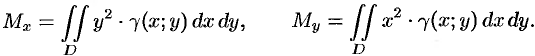
Момент инерции фигуры относительно начала координат — по формуле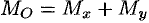 
.
Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример №53.3.
Найти объем тела, ограниченного поверхностям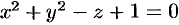и 
и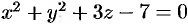 
.
Решение:
Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
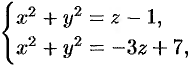
находим уравнение линии их пересечения: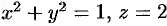 
.
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг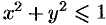 
) и ограниченных сверху соответственно поверхностям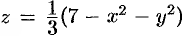и 
и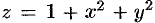 
. Используя формулу (53.4), имеем
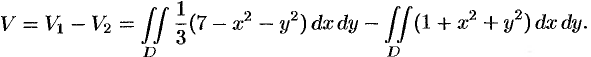
Переходя к полярным координатам, находим:
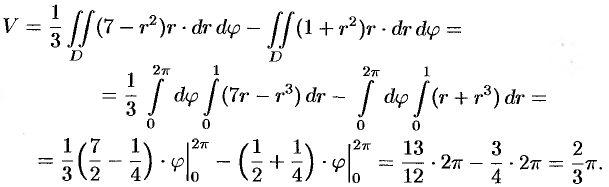
Пример №53.4.
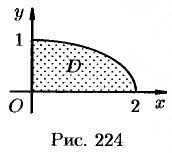
Найти массу, статические моменты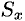 
и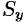 
и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом 
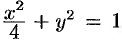и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
Решение:
По формуле (53.6) находим массу пластинки. По условию,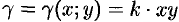 
, где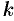 
— коэффициент пропорциональности.
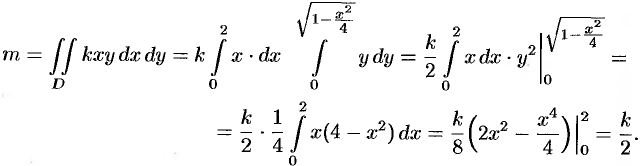
Находим статические моменты пластинки:
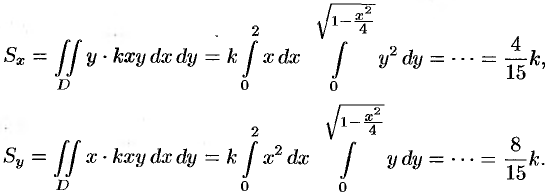
Находим координаты центра тяжести пластинки, используя формулы
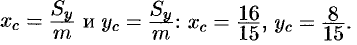
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
