Оглавление:
При нахождении площадей плоских фигур, ограниченных некоторыми линиями, удобно использовать следующий алгоритм:
- Построить фигуру, площадь которой требуется найти.
- В соответствии с таблицей 23.1. определить вид фигуры и составить формулу для вычисления площади фигуры. Следует обратить внимание на границы интегрирования. Если они не следуют непосредственно из условия задачи, а определяются пересечением графиков каких-либо функций, то границы
интегрирования следует находить аналитически, приравнивая соответствующие функции. - Вычислить площадь фигуры. Следует помнить, что площадь есть число положительное.
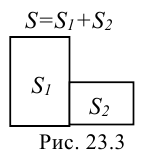
При составлении таблицы 23.1. учитывалось свойство аддитивности площади: если фигура состоит из двух и более частей, то для нахождения площади фигуры нужно сложить площади ее частей (рис. 23.3).
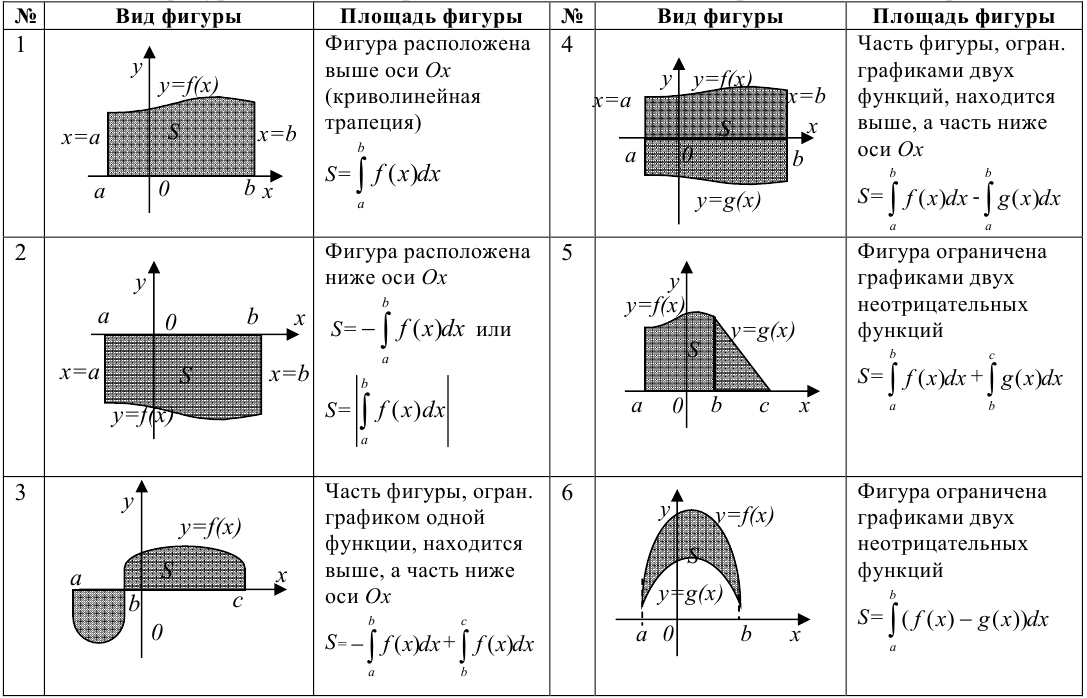
Таблица 23.1
Виды фигур, площадь которых находится с помощью определенного интеграла
Пример №23.1.
Найдите площадь фигуры, ограниченной линиями 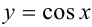 , отрезком
, отрезком 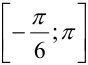 оси
оси 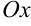 , прямыми
, прямыми 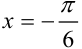 и
и 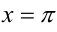 .
.
Решение:
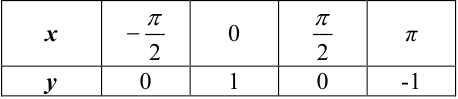
1. Построим заданную фигуру. График функции 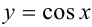 — синусоида, строится с использованием следующих характерных точек:
— синусоида, строится с использованием следующих характерных точек:
Прямые 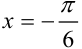 и
и 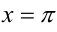 проходят через соответствующие точки и параллельны оси
проходят через соответствующие точки и параллельны оси 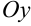 . В итоге получим фигуру, обозначенную штриховкой на рис. 23.4.
. В итоге получим фигуру, обозначенную штриховкой на рис. 23.4.
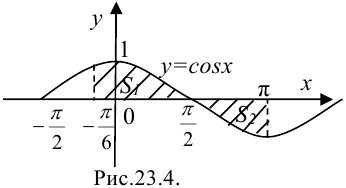
2. Согласно таблице 23.1. рассматриваемая фигура соответствует 3 типу. Её площадь находится как сумма площадей двух частей фигуры: части, находящейся выше оси  , и части, находящейся ниже оси.
, и части, находящейся ниже оси.
Площадь части, находящейся выше оси  , можно найти по формуле
, можно найти по формуле 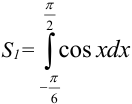 .
.
Площадь части, находящейся ниже оси 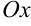 , можно найти по формуле
, можно найти по формуле 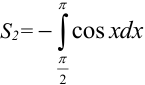 .
.
Вычислим 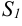 и
и 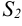 :
: 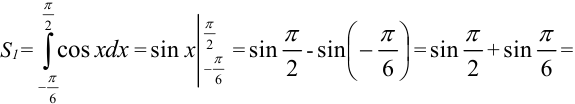
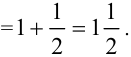
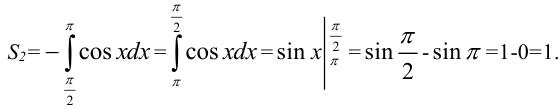
Для нахождения общей площади 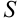 , сложим значения
, сложим значения 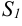 и
и 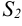 :
: 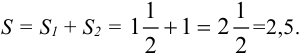
Ответ: 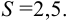
Пример №23.2.
Найдите площадь фигуры, ограниченной линиями 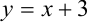 и
и 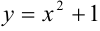 .
.
Решение:
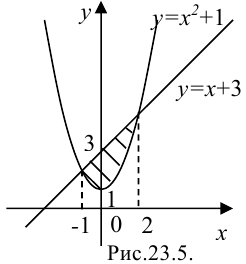
1. Построим фигуру, ограниченную графиками функций 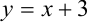 и
и 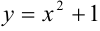 (рис. 23.5). Линия, задаваемая уравнением
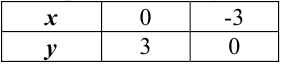
(рис. 23.5). Линия, задаваемая уравнением 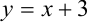 — прямая. Построим ее по двум точкам.
— прямая. Построим ее по двум точкам.
1. Построим фигуру, ограниченную графиками функций 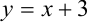 и
и 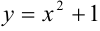 (рис. 23.5). Линия, задаваемая уравнением
(рис. 23.5). Линия, задаваемая уравнением 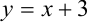 — прямая. Построим ее по двум точкам.
— прямая. Построим ее по двум точкам.
Линия, задаваемая уравнением 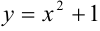 — парабола, ветви которой направлены вверх. Построим ее методом преобразований: выполним параллельный перенос графика функции
— парабола, ветви которой направлены вверх. Построим ее методом преобразований: выполним параллельный перенос графика функции 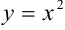 на 1 единицу вверх.
на 1 единицу вверх.
Получили фигуру, ограниченную двумя графиками функций.
2. Согласно таблице 23.1. рассматриваемая фигура соответствует 6 типу. Её площадь можно вычислить по формуле: 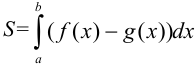 , где
, где  — функция, ограничивающая фигуру «сверху» (
— функция, ограничивающая фигуру «сверху» (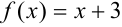 ), a
), a 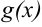 — функция, ограничивающая фигуру «снизу» (
— функция, ограничивающая фигуру «снизу» (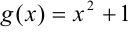 ).
).
Границы интегрирования 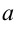 и
и 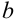 в данном случае не следуют непосредственно из условия задачи. Решив уравнение
в данном случае не следуют непосредственно из условия задачи. Решив уравнение 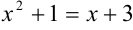 , мы найдем абсциссы точек пересечения графиков соответствующих функций, т.е.
, мы найдем абсциссы точек пересечения графиков соответствующих функций, т.е. 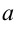 и
и 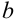 .
.
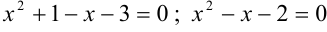 . Найдем корни уравнения по теореме, обратной теореме Виета:
. Найдем корни уравнения по теореме, обратной теореме Виета: 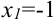 или
или 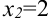 . Следовательно,
. Следовательно, 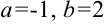 .
.
Составим формулу для вычисления площади искомой фигуры: 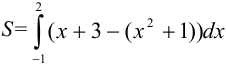 .
.
3. Вычислим значение площади:
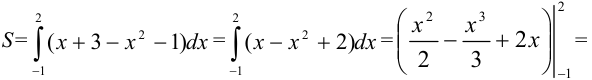
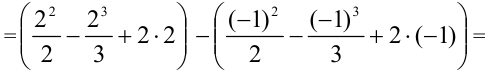
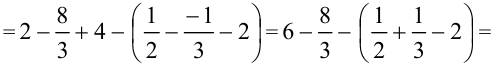
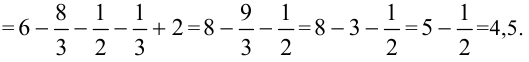
Ответ: 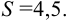
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Интегрирование по частям. |
| Геометрический смысл определенного интеграла |
| Вычисление длины дуги плоской кривой и объема тел вращения. |
| Понятие несобственного интеграла |

