Оглавление:
Как уже отмечалось, дифференциальные уравнения находят широкое применение в практической деятельности человека. Рассмотрим некоторые задачи, сводящиеся к решению дифференциальных уравнений.
Пример №38.6.
Составить уравнение линии, проходящей через точку 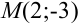 и имеющей в каждой точке угловой коэффициент касательной
и имеющей в каждой точке угловой коэффициент касательной 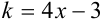 .
.
Решение:
Обратимся к геометрическому смыслу производной: 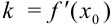 или
или 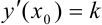 . Поскольку
. Поскольку 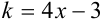 задано в условии задачи, то можно составить уравнение:
задано в условии задачи, то можно составить уравнение:
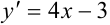 — простейшее дифференциальное уравнение первого порядка.
— простейшее дифференциальное уравнение первого порядка.
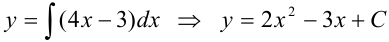 — семейство линий, имеющих в каждой точке угловой коэффициент касательной
— семейство линий, имеющих в каждой точке угловой коэффициент касательной 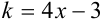 .
.
Выделим уравнение одной линии, проходящей через точку 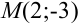 . Подставим в уравнение
. Подставим в уравнение 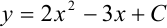 значения
значения 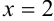 и
и 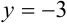 :
:
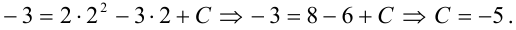
Получили, что 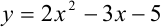 — уравнение линии, проходящей через точку
— уравнение линии, проходящей через точку 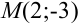 и имеющей в каждой точке угловой коэффициент касательной
и имеющей в каждой точке угловой коэффициент касательной 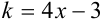 .
.
Ответ: 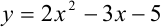 .
.
Пример №38.7.
Тело движется прямолинейно со скоростью 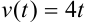 . Найдите закон движения тела, если при
. Найдите закон движения тела, если при 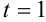 тело находилось в начале координат.
тело находилось в начале координат.
Решение:
Воспользуемся физическим смыслом производной: 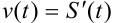 . Поскольку
. Поскольку 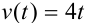 задано в условии задачи, то можно составить уравнение:
задано в условии задачи, то можно составить уравнение:
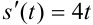 — простейшее дифференциальное уравнение первого порядка.
— простейшее дифференциальное уравнение первого порядка.
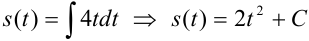 — общее решение дифференциального уравнения.
— общее решение дифференциального уравнения.
Найдем частное решение этого уравнения. Поскольку по условию при 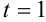 тело находилось в начале координат, подставим в уравнение
тело находилось в начале координат, подставим в уравнение 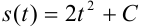 значения
значения 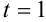 и
и 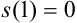 :
:
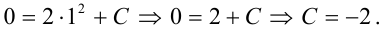
Подставляя 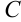 в общее решение, получим, что
в общее решение, получим, что 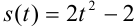 — искомый закон движения тела.
— искомый закон движения тела.
Ответ: 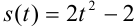 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

