Оглавление:
Причины возникновения ускорения Кориолиса и его определение
Кориолисово ускорение появляется только при непоступательном движении подвижной системы, почему ею и называют иногда поворотным ускорением.
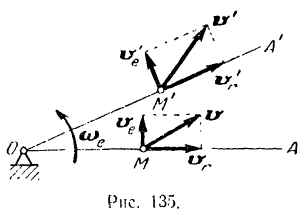
Рассмотрим такой простой пример. Точка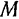 
движется равномерно по прямолинейному отрезку 
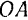, который, и свою очередь, вращается с постоянной угловой скоростью 
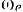вокруг неподвижной точки 
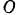. Пусть в момент времени 
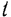точка занимает положение 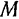на радиусе 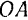, а в момент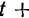 
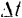— положение 
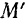на радиусе 
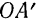(рис. 135).
Если бы переносное движение подвижной системы 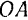отсчета было поступательным, то переносная скорость точки 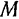не зависела бы от се положения на радиусе 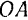, а следовательно, и от относительного движения точки. Но при вращательном движении подвижной системы модуль переносной скорости точки изменяется, вследствие ее относительного движения по радиусу 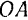, за время 
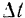от значения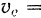 
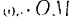до значения
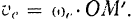
Так как в данном случае движение точки относительно подвижного радиуса — прямолинейное и равномерное. го ее относительное ускорение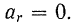 
. Однако вследствие переносного крашения радиуса 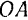постоянная по модулю (в данном случае) относительная скорость точки изменяет свое направление за время 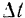от значения 
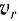до значения 
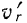(рис. 135), поворачиваясь в сторону переносного вращения.
Таким образом, возникновение корнолиеова ускорения обусловливается взаимным влиянием относительного и непоступательного переносного движений точки на изменение вектора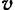 
ее абсолютной скорости.
Как было найдено в § 57, кориолисово ускорение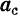 
равно удвоенному векторному произведению угловой скорости 
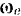переносного движения на относительную скорость 
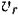точки
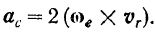
Исходя из свойств векторного произведения двух векторов, находится модуль и направление ускорения Кориолиса:
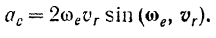
Модуль ускорения Кориолиса равен удвоенному произведению модуля 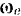угловой скорости переносного движения на модуль 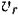относительной скорости точки и на синус угла между этими векторами.
Из формулы (96) следует, что кориолисово ускорение равно нулю в случаях:
1) когда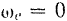 
, т. е. в случае поступательного переносного движения пли в моменты, когда угловая скорость непоступательного переносного движения обращается в пуль;
2) когда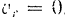 
. т. е. в случае относительного покоя точки пли в моменты, когда се относительная скорость обращается в пуль;
3) когда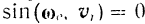 
, т. е. в случае, когда относительная скорость 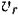точки в рассматриваемый момент параллельна оси 
переносного вращения.
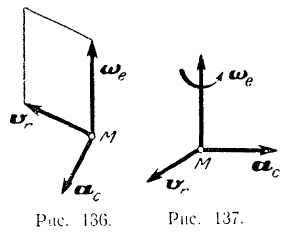
Для того чтобы определить направление вектора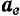 
кориолисова ускорения точки 
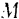, нужно перенести в данную точку (параллельно самому себе) вектор 
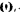, переносной угловой скорости, восстановить в этой точке перпендикуляр к плоскости, в которой лежат векторы 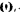, и 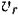и направить его в ту сторону, откуда кратчайший переход от вектора 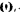, к вектору 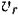был бы виден совершающимся против ходе-стрелки часов (рис. 136).
Пели относительное движение точки происходит в плоскости, перпендикулярной к оси переносного вращения (рис. 137), то
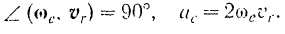
Направление вектора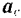 
можно найти в этом случае, повернув вектор 
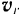относительной скорости точки на угол 90 в сторону переносного вращения.
Пример задачи:
Шарик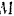 
движется вдоль трубки, расположенном и вертикальной плоскости 
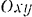(рис. 1:18). с постоянной относительной скорости 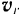, а сама трубка вращается с постоянной угловой скоростью 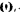, вокруг горизонтальной оси проходящей через точку 
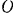. В начальный момент шарик находился в точке 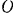трубки. Определить абсолютное ускорение шарика в момент времени .
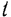Решение:
Движение шарика по отношению к неподвижной системе отсчета 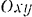(абсолютное движение) можно рассматривать состоящим из двух движений: движения шарика вдоль подвижной трубки (относительное движение) и его движения вместе с трубкой (переносное движение). Так как переносное движение является вращательным, то абсолютное ускорение шарика определяется по формуле (94):
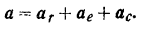
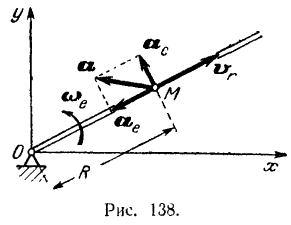
Движение шарика вдоль трубки есть равномерное и прямолинейное движение, поэтому его относительное ускорение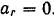 
Так как трубка вращается с постоянной угловой скоростью, то переносное вращательное ускорение
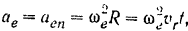
где расстояние точки 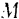от оси вращения в момент 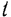равно
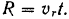
Направлено переносное ускорение
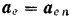
по радиусу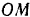 
к центру .
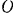Относительное движение шарика происходит в плоскости, перпендикулярной оси вращения, следовательно, модуль кориолисова ускорения
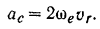
Для того чтобы определить его направление, достаточно повернуть в этом случае вектор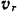 
относительной скорости точки на угол 90 в сторону переносного вращения (как показано на рис. 138).
Абсолютное ускорение шарика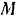 
определится как диагональ параллелограмма, построенного на векторах 
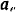и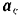 
. Модуль его
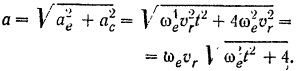
Пример задачи:
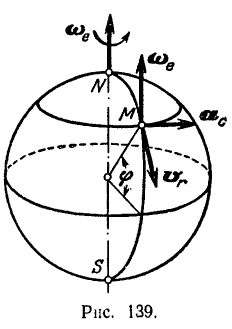
Точка движется по поверхности Земли с севера на юг с постоянной относительной скоростью
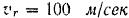
вдоль меридиана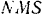 
(рис. 139). Найти кориолнеово ускорение 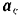точки 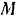, когда она находится на широте
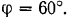
Решение:
Так как Земля вращается с запада на восток, то вектор 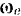угловой скорости Земли надо отложить по оси вращения Земли в направлении от южного полюса к северному.
Модуль этой угловой скорости
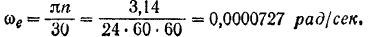
Для определения направления вектора 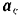кориолисова ускорения перенесем вектор 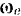в точку 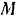. Вектор 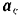будет направлен перпендикулярно к плоскости, проходящей через векторы 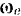и 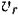и в такую сторону, чтобы кратчайший переход от 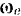к 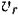совершался против хода стрелки часов, т. е. по касательной к соответствующей параллели с запада на восток. Модуль кориолисова ускорения согласно формуле (96) будет равен
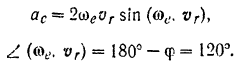
Следовательно, в данном случае:
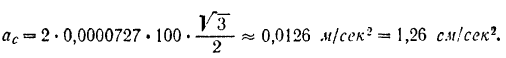
Как видим, вследствие малости угловой скорости вращения Земли величина кориолисова ускорения, возникающего благодаря вращению Земли, получается весьма небольшой. Поэтому в-тяпнем вращения Земли на движение тел по поверхности или вблизи поверхности Земли, происходящих не с очень большими скоростями и не слишком долгое время, обычно можно пренебречь.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Теорема о сложении скоростей + пример с решением |
| Теорема Кориолиса о сложении ускорений + пример с решением |
| Понятие плоского движения тела |
| Уравнения движения плоской фигуры + пример с решением |
