Оглавление:


Приближённый метод вычисления моментов инерции площади
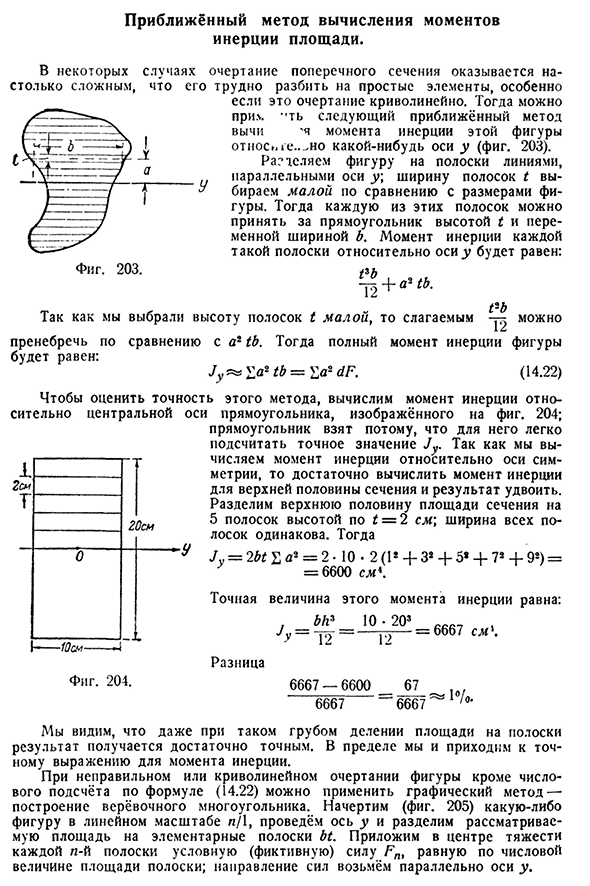
- Аппроксимационный метод расчета момента инерции участка. В некоторых случаях профиль поперечного сечения очень сложен, и его трудно разбить на простые элементы, особенно если профиль изогнут. Тогда ты его забираешь. Следующий приближенный метод оценки момента инерции этой фигуры является относительным.. >Но некоторые оси y(рис. 203). Ширина полосы Т выбирается меньше размера рисунка. И каждая из этих полос может быть
прямоугольником с высотой t и переменной шириной B.:. «fib» можно игнорировать по сравнению с a2tb. Тогда сумма моментов инерции на рисунке выглядит следующим образом: Потому что мы выбрали (14.22) Дя^^a2tb=в a2dF. Для оценки точности этого метода рассчитаем момент инерции относительно центральной оси прямоугольника, изображенного на рисунке. 204; прямоугольник берется,
так как для него легко вычислить точное значение Jy. Вычислите момент Людмила Фирмаль
инерции для оси симметрии, достаточно вычислить момент инерции в верхней половине сечения и удвоить результат. Разделите верхнюю половину площади поперечного сечения на 5 полос£=2 см высоты\ширина всех полос одинакова. Тогда J=2bt S a2= 2* 10 • 2(12 + 32 + 5′ + 72 + 92) = = 6600 slg4 Точные значения для этого момента инерции являются: =6667SL<4. Разница 6667-6600_67 1Р/ 6667 — 6667
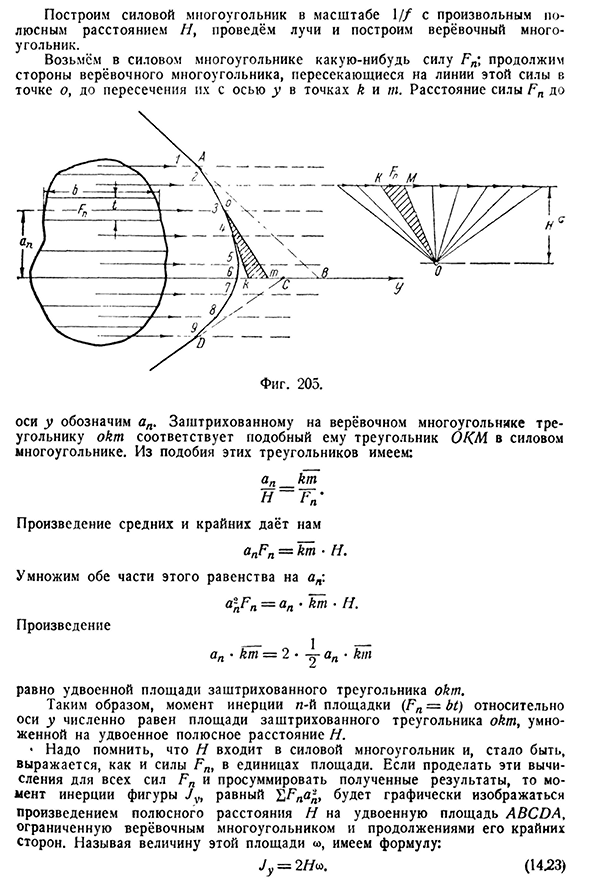
1=3 / o-даже при таком грубом делении площади на полосы видно, что результат достаточно точен. На пределе это будет точное представление момента инерции. Если форма нерегулярная или криволинейная, то помимо численных расчетов по формуле (14.22) можно применить графический метод (построение канатного многоугольника) рисования (рис. 205) любая фигура на линейном масштабе n / 1 рисует ось y и делит область, которая считается
- основной полосой bt. Применим к центроиду каждой l-й полосы условную (фиктивную) силу Fn, равную численному значению площади полосы; примем направление силы, параллельное оси Y.§ 88] метод аппроксимации 289 для вычисления момента инерции Построим силовой полигон масштаба 1//с любым расстоянием между полюсами, проведем линию и построим канатный полигон. Рассмотрим некоторую силу Fn в силовых полигонах; мы можем
видеть, что на этой силовой линии в точке o они пересекаются с осью y в точке k и T. оси Y, обозначается АП. Треугольник okm, заштрихованный канатным многоугольником, соответствует аналогичному треугольнику около км силового многоугольника. Из сходства этих треугольников мы имеем: АР Произведение среднего и экстремального значения дает нам anFn-km-H. Умножьте обе части этого уравнения на_ » /. 1 я в р J Я V я у Джей У. Я n1V1LM н д
Удобно сделать высоту полосы одинаковой, но все Fn пропорционально ширине полосы. ПлощадьЛюдмила Фирмаль
планиметра. Нет необходимости преследовать несколько полос; мы видели выше, что достаточная точность достигается с относительно широкой полосой. Следует помнить, что описанный способ основан на пренебрежении собственным центральным моментом инерции полосы. Применим результаты, полученные в этой главе, к задаче испытания на прочность балки с более сложным поперечным сечением.
Смотрите также:

