Приближенные уравнения для малых чисел Рейнольдса. Плоские ползущие течения

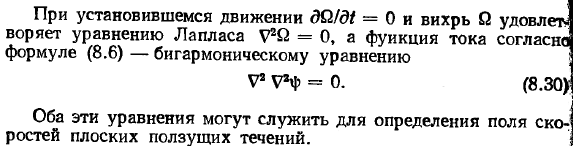
Приближенные уравнения для малых чисел Рейнольдса. Плоские ползущие течения

Приближенные уравнения для малых чисел Рейнольдса. Плоские ползущие течения Решение конкретной задачи, рассматриваемой ниже, является приближенным, но экспериментальным.. Степень приближения к принципу вполне достаточна и может быть использована в технических расчетах. Тем не менее, следует подчеркнуть, что для того, чтобы уверенно использовать приближенные решения, необходимо, чтобы условия и допущения, на основе которых они получены, были в достаточной степени выполнены в каждом конкретном случае.

Интуитивное соображение состоит в том, что для малых скоростей потока и большой вязкой инерции уравнения конвекции Навье-Стокса малы и пренебрежимо малы по сравнению с уравнениями вязкости. Людмила Фирмаль

• Это предположение можно обосновать, представив уравнение Навье-Стокса в безразмерном виде. Анализ такого безразмерного уравнения показывает, что вязкий член может быть во много раз больше малого числа Рейнольдса, то есть конвективного члена Ke = aB / x 0 1 122]. Течение под Ke 1 называется ползучим. Когда боковые размеры канала малы и вязкость жидкости высока, это происходит во многих конструктивных элементах машин, оборудования и оборудования. equipment.

• В этих случаях мы видим, что практически возможно исходить из уравнения Навье・Стокса без учета конвективного члена. Предполагая, что массовая сила постоянна, дифференцирует первое уравнение относительно x, дифференцирует 2-е уравнение относительно y, дифференцирует 3-е уравнение относительно r и складывает их вместе. Рассматривая уравнения неразрывности 0НУ и −0、 08-28） То есть гармоника function. In нестационарное движение.

Следовательно, давление потока ползучести удовлетворяет уравнению Лапласа. Людмила Фирмаль

• Время (которое явно не входит в Формулу (8.28)) играет роль параметра, а формула(8.28) определяет мгновенное поле давления. Уравнения для определения поля скоростей плоского течения могут быть получены из уравнения (8.5)без учета конвективного члена. Устойчивое движение делаем.！При D1 = 0 вихрь заполняется. Потоковая функция основана на использовании уравнения Лапласа V2Y = 0 и выражения (8.6) уравнения двоичной суммы В * =0.(8.30） Оба этих уравнения помогают определить поле скоростей планарной ползучести.

Смотрите также:

Учебник по гидравлике

Возможно эти страницы вам будут полезны:

1. Ламинарное течение между соосными вращающимися цилиндрами.
2. Диффузия вихрей в вязкой жидкости.
3. Течение вязкой жидкости в тонком слое переменной толщины. Уравнения Рейнольдса для смазочного слоя.
4. Плоский клиновидный смазочный слой.