Оглавление:








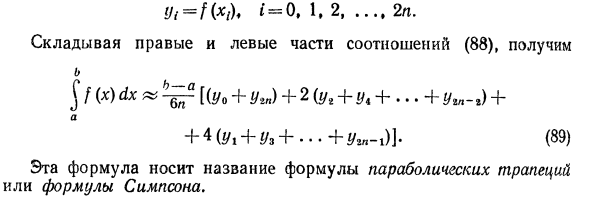



Приближенные методы вычисления определенных интегралов
- Приближенный метод вычисления определенного интеграла /. Общий комментарий. Постановка вопроса. б Предположим, нам нужно вычислить определенный интеграл от / = J f (n) dx. но Непрерывная функция j (x). Если обратная производная F (x) подынтегральной функции найдена согласно формуле Ньютона Лейбница б \ f (x) dx = F (b) -F (a) но Если антипроизводная не найдена или если функция y-f (i) задана в графической или табличной форме, используйте формулу аппроксимации для вычисления интеграла. Его точность может быть произвольно увеличена.
По этой причине задача приближенного вычисления интегралов эквивалентна задаче приближенного вычисления искривленных трапециевидных областей. Идея приближенных интегральных вычислений состоит в том, что кривые y — f (x) заменяются новыми кривыми, которые «достаточно близки».
Метод аппроксимации для вычисления конкретного интеграла В большинстве случаев конкретная интеграция б \ f (x) dx численно равен площади изогнутой трапеции, но Вертикальная линия через кривую y-f (x), сегмент оси Ox [a, b] и точки x-a и x-b. Людмила Фирмаль
Желаемая площадь тогда приблизительно равна площади изогнутой трапеции, окруженной новой кривой. Для этой новой граничной кривой выбирается та, которая просто вычисляет площадь трапеции кривой. Получите ту или иную приближенную интегральную формулу в зависимости от выбора новой кривой.
Теперь рассмотрим изогнутую трапецию, окруженную произвольной кривой y = f (x) (рис. 210). Через точку Mg (xd \ ul) xn = ■ = b, pro Mg (xc; yc) tM9 (xn; yn) для этой кривой, где xd = a, xc = Введена вспомогательная парабола y-Ax2 + Bx-j-C. Такую параболу всегда можно провести через три точки, и можно использовать только одну (см. Главу 6, § 9, Замечания). Площадь изогнутой трапеции, окруженной вспомогательной параболой, приблизительно равна площади данной изогнутой трапеции. б б Тем не менее, Согласно уравнению (86) б J (Ax »+ Bx + C) dx = (y, + 4Uc + y„), но
| Кривизна плоской кривой | Функции нескольких переменных |
| Несобственные интегралы | Предел функции нескольких переменных» непрерывность функции. Точки разрыва |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Тогда для любой функции y = f (x) выполняется следующее приближенное уравнение: б Jb — o f M dx «- (str + Aus + ya). но Однако, если отрезок [a, b] достаточно велик, аппроксимация, определяемая уравнением (86), будет слишком грубой. Таким образом, б Чтобы получить более точное приближение интеграла J f (x) dx, но Действуйте следующим образом: Разделите сегмент [a, b] на четные числа Количество маленьких отрезков, равных 2n длины A = xv xv х3, разделительная точка.
Эти сегменты будут точками xJt x3 и hgp_g соответственно б Разделим интеграл J f (x) dx на сумму нескольких интегралов. но B xg x4 xtn \ jf (x) dx = <\ f (x) dx + ‘\ f (x) dx + … + I f (x) dx (87) б — а 6 н J f (x) dx (Ugp-g + b Ugp-x + Ugp) * игры X! L% —1 Примените уравнение (86) к каждому интегралу справа от уравнения (87). j / (x) dx \ (y 0 + 4 yx -f yt) \
Рассмотрим короткие отрезки [x0, xt] 9 [xr, x4], …, [x.2n.tt xtn] (x0 = a, x.2n = b); середина Людмила Фирмаль
lJi — f (* /) ♦ ‘= 0, 1,2 ….. 2l. Добавление правой и левой части соотношения (88) приводит к следующему: «b ^ [С ^ / о4- </ *„) 4-2 (год 4 «! / 4 + … 4-год-%) 4- но + 4 4-Уз + ••• 4- Ут-и)] »(89) Эта формула называется параболической или формулой Симпсона. Для оценки погрешности расчета с использованием уравнения Симпсона можно рекомендовать следующее уравнение: б f (x) dx-I „| <I7» -7 «‘, (90) но Где / 2I и / 4n — результаты вычисления интеграла числа делений на 2n и 4n частей интегрального сегмента согласно формуле Симпсона соответственно.
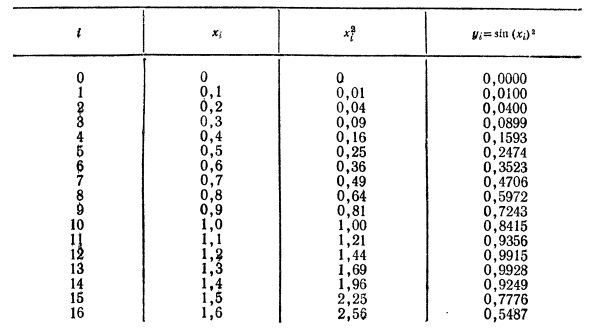
Пример расчета по формуле Симпсона Другими словами J грех (х2) дх о 2π = 4 и 2/2 = 8 Решения. Составьте таблицу с 2n = 4 и h = x 0,4 (Таблица 3) Таблица 3 1 4 l / i = ”Jn (* i)” 0 0 0,00 0,0000 1 0,4 0,16 0,1593 2 0,8 0,64 0,5972 3 1,2 1,44 0,9915 4 1,6 2,66 0,5487 Используйте уравнение (89) для получения: Другими словами j sin (x2) dx [y / o + Y, + 4 (yy + uz) +2; / 2] = о = [0 + 0,5487 + 4 (0,1593 + 0,9915) + 2 • 0,5972] = 0,8462. Если 2n = 8 и = 1.6 ° = 0.2, используйте таблицу. 1, мы получаем 1,8 б — а ] sin (x2) dx «[y0 -f y9 + 4 (y, + y3 + ul + y7) + 2 (yy + * /, -} — //»))]] о = [0 -f- 0,5487 + 4 (0,0400 + 0,3523 + 0,8415 + 0,9249) -f- + 2 (0,1593 -f 0,5972 + 0,9915)] = 0,8455. Если вы сравните результаты обоих вычислений, вы увидите, что они совпадают после округления первых трех символов. Поэтому для приближенных интегральных значений Другими словами j sin (l2) dx w 0,846
Напомним, что табличное значение для этого интеграла с точностью до 0,00001 составляет 0,84528. Замечания. Метод Симпсона обычно дает более точные результаты, чем трапециевидный метод, если число точек разделения сегмента интегрирования одинаково. Это показывает, что трапециевидная ошибка обратно пропорциональна квадрату числа точек деления, а ошибка метода Симпсона обратно пропорциональна четвертой степени числа точек деления.
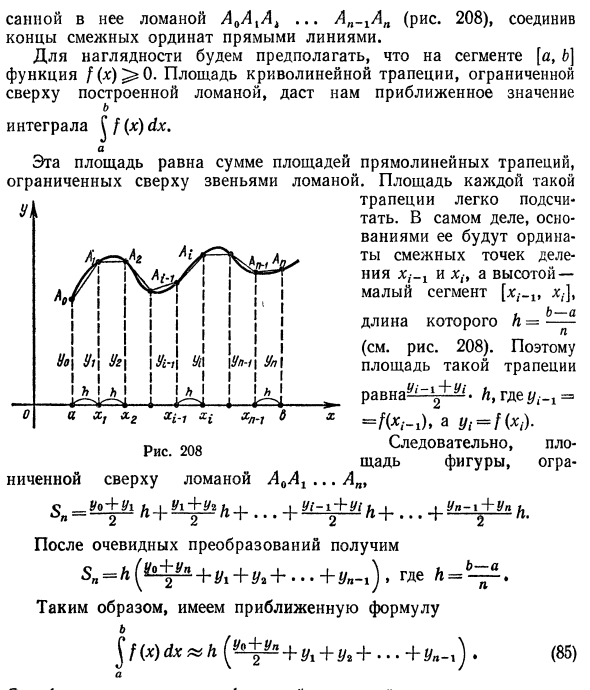
Трапециевидный метод б Предположим, нам нужно вычислить определенный интеграл / = ^ / (η 🙂 dx. но Разбейте интегральный сегмент [a, b] на n равных небольших сегментов, разбив точки xv xr, .xit …, xn -v. Кроме того, x0 = a, xn-b. Длина h каждого маленького отрезка равна Нарисуйте прямую линию, параллельную оси Oy через точку разделения. Скрестите их с кривой в точках A0, Alt Ar, Ait An-X% An. Заменить эту кривую y = f (x) на Пунктирная линия A0AlAi … Ap-xAn (рис. 208), соединяющая соседние концы ординат прямой линией. Для наглядности предположим, что функция f (x) ^ 0 на отрезке [a, b]. Площадь трапеции, окруженная пунктирной линией выше, дает приблизительное значение Рис. 208 Верхняя пунктирная линия A0Ag , Интеграция J f (x) dx.
Эта площадь равна сумме площадей прямой трапеции, окруженной прямой связью. Каждая такая область Трапеции легко подсчитать. Фактически, смежная точка разбиения и ордината xit становятся ее базовой точкой, и небольшим сегментом [xt ^ v Длина h = (См. Рис. 208). Поэтому площадь такой трапеции ^ Равно j L, где = = / (*, -1), a * /, = / (*,). В результате площадь фигуры N После очевидного преобразования получим следующее Sa = h (до ± ^ + yl + y1 + … + yn-1), где Λ = Так что есть формула аппроксимации Эта формула называется трапеция.
Трапециевидная формула, оцененная в предположении, что / (*)> 0 действительна для функции f (x) t, продолжающейся в сегменте [i, b]. Очевидно, что с увеличением числа n точек в расщеплении точность, определяемая формулой трапеции, возрастает. При вычислении интеграла с использованием трапециевидной формы вы обычно делаете следующее: 1) Рассчитать интегральное значение / л и количество точек деления n и 2n. 2) Сравните результаты расчета и оставьте все признаки, которые соответствуют первым.
l.e Пример, вычислить интеграл J sin (x2) dx по формуле о Предполагаемая трапеция, 8 8 и η> 16. Решения. Составляет таблицу значений подынтегральных Функция с h = x8 и h = » = = 0.2 (таблица 1). Таблица 1 1 * 1 4 0 0 0 0,0000 1 0,2 0,04 0,0400 2 0,4 0,16 C ‘, 1593 3 0,6 0,36 0,3523 4 0,8 0,64 0,5972 5 1,0 1,00 0,8415 6 1,2 1,44 0,9915 7 1,4 1,96 0,9249 8 1,6 2,56 0,5487 Из формулы (85) n * = * 8, Другими словами Jsin ^^^ A ^ Sii ^ + ^ + ^ + j / .+^+ y. + ^ + n = 0 = 0,2 р + b’5487 + 0,04 00 4-0,1593 + 0,3523 + 0,5972 + 0,8415 + + 0,9915 + 0,9249] -0,2,4,1807 = 0,8362. Затем составьте таблицу значений подынтегральных функций для -16 и h = ■ 1 = 0.1 (таблица 2). Таблица 2
т * ф 0 0 1 0,1 9 0,2 с 0,3 4 0,4 б 0,5 е 0,6 7 0,7 8 0,8 д 0,9 10 1,0 1,1 12 1,? 13 1,3 14 1,4 15 1,5 16 1,6 Ну? ftBSillUi) ‘ 0 0.0000 0,01 0,0100 0,04 0,0400 0,09 0,0899 0,16 0,1593 0,25 0,2474 0,36 0,3523 0,49 0,4706 0,64 0,5972 0,81 0,7243 1,00 0,8415 1,21 0,9356 1,44 0,9915 1,69 0,9928 1,96 0,9249 2,25 0,7776 2.5a 0.5487 Применяя уравнение (78), когда n = 16: Другими словами J sin (x <) dxtt ^ [0 + 02’5487 + 0,0100 + 0,0400 + 0,0899 + 0,1593+ о + 0,2474 + 0,3523 + 0,4706 + 0,5972 + 0,7243 + 0,8415 + + 0,9356 + 0,9915 + 0,9928 + 0,9249 + 0,7776] = 0,8429. Если вы сравните результаты обоих вычислений, вы увидите, что они совпадают после округления первых двух знаков. Поэтому для приближенного значения интеграла
Другими словами ^ грех (х1) дх и 0,84 о Значение этой таблицы интеграции с точностью 0,00001 составляет 0,84528. 3. Параболический трапециевидный метод (метод Симпсона ) Этот метод для приближенного вычисления конкретного интеграла основан на замене графа подынтегральной функции параболической дугой, ось которой параллельна оси Oy, а не хордой, подобной трапециевидному методу. Прежде чем описывать этот метод, рассмотрим конкретный случай, когда кривая, ограничивающая данную трапецию кривой, является биномиальным троичным графом # = / () = Ax2 + + Yl: + C Имеет место следующая формула: б J (Ax ‘+ Bx + C) dx = l- (str + 4us + y „), (86)
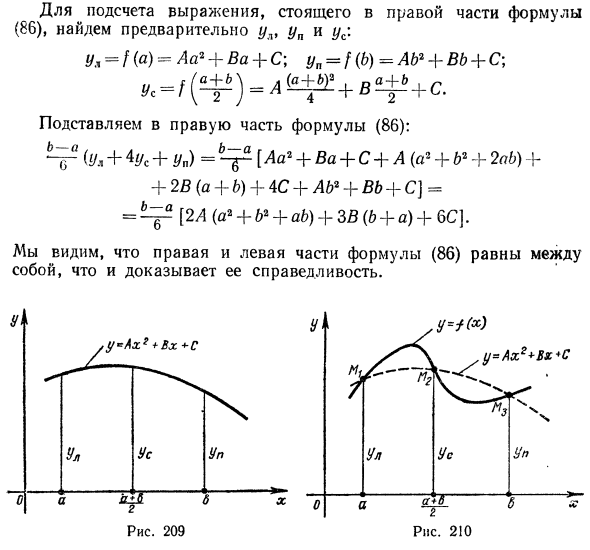
Где st — ордината кривой в точке x-a (левая ордината). yn — ордината (правая ордината) кривой в точке x-b. // c — ордината кривой в средней точке отрезка [a, b] Это значит Точка х (рис. 209). Вывод этой формулы ограничен прямой проверкой. Подсчитайте левое выражение времени в выражении: но = тз? [2a (b + ab + a2) + 3B (b + a) + 6C].
Чтобы вычислить выражение в правой части уравнения (86), сначала найдите ul, yn и yn. y4 = f (a) = Aa * + Ba + C; y = f (b) = AB * + B + C; Присвойте правой части уравнения (86). PG (+ + Yn) = Tsr [A * + Ba + C + A (<a2 + b2 + + + 2B (a + b) + 4C + A2 + B + — +]] = [2/4 (a2- Bb2 + a6) -1-3B (& + a) + 6C]. Найдено, что правая и левая части уравнения (86) равны друг другу, и их обоснованность доказана.

