Оглавление:


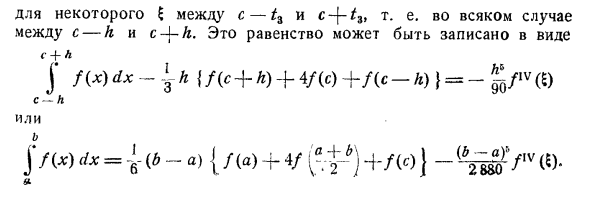
Приближенные формулы для определенных интегралов. Правило Симпсона
- Примерное выражение для конкретного интеграла. Правило Симпсона Есть несколько приближений для некоторых интегралов, которые играют важную роль в расчете. Самый простой из них: б jj mdxc * -L (b-a) {f (a) + f (b)}. (1) но Теперь замените область PXNXNP (см. §148) на область трапеции PiNxNP. Если / () — линейная функция, выражение является точным. Если f (x) имеет производные f ‘(x) и / «(), ошибка в (1) будет следующей (см. Пример LXVII.2, с.328): Z — значение x между a и b.
Замечательно хороший рецепт б J-J <* — а) {/ (α) + 4 / (Ц ±) + / ()}. (2) но Эта формула известна как правило Симпсона. Если f (x) имеет четыре производных / ‘() «/’ (*)» / «‘С *) и / IVC *)», то ошибка в (2) —Riso ^ —a> V, v (£)
Конечно, в реальных вычислениях вам нужно разделить интервал интегрирования на меньшие секции и применить эту формулу к каждой секции по отдельности. Людмила Фирмаль
Некоторые я между а и б. В частности, это показывает, что правило Симпсона дает точные результаты для полиномов третьего порядка и ниже. напишите -h> c ~ \ -h вместо a> b и подумайте о функции где с-н * (0 = J / (*) dx-s / {f (c-f /) + 4 / (6) + f (c- /)} S-I Дифференцируя три раза, 9 ‘(O = | {/ («+ O-2 / (e) + / (» -0} — —J./ {/ ‘(<- • -B-Oj-Jf * (A) .Φ «</’ (<- • + о- / Ч’-о} — -111 г (с + о н-г («-о} * (L)», 9 ‘»СО = -1 мГ (е + О- / » («-0} — ^ ♦ (Л).
| Площадь сектора круга. Круговые функции | Интегралы от комплексных функций действительного переменного |
| Общие свойства определенного интеграла | Cходимость бесконечных рядов и несобственных интегралов |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Следовательно, теорема о среднем значении 9 «‘(0 = -} / 1 {/, v (£) + ^ W}, (3) Где ξ находится в интервале (c- /, c -) — /). Однако, поскольку 9 (0) = 9 (A) = 0, теорема о роли приводит к 9 ‘(,) = () для некоторого tXy между 0 и h. Так как 9 ‘(0) = 0, 9 «(^) = 0 при некотором t9 между 0 и /„. Так что это между 0 и ч. Наконец, cp «(0) = ^ = 0 и, следовательно, 9 » (£ 3) = 0 для некоторого t3 между 0 и A. G (5) = -S * (A)
Некоторые $ между c- и c- (то есть любой случай между c-h и c — \ — h. Это уравнение можно записать в виде j / (*) dx {/ (s + h) + 4 / (s) + / (s- / *)} = -g / iv (g) s— И ИЛИ б J / C ) «< = 6- (6-a) {/ (a) +4 / (? + *) 4- / (c)) — («).
В фактическом расчете снова разделите интервал интегрирования на части и примените правило Симпсона к каждой части. Людмила Фирмаль

