Оглавление:






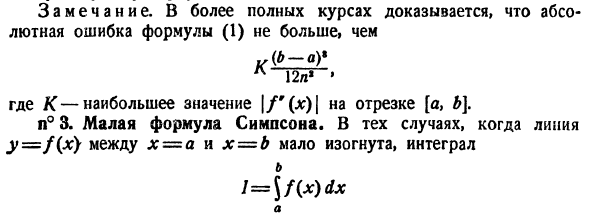

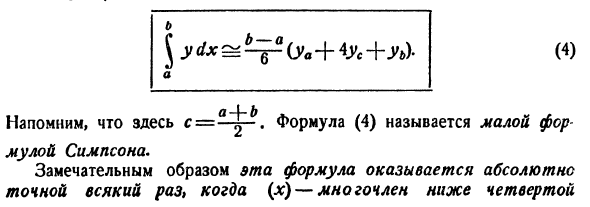





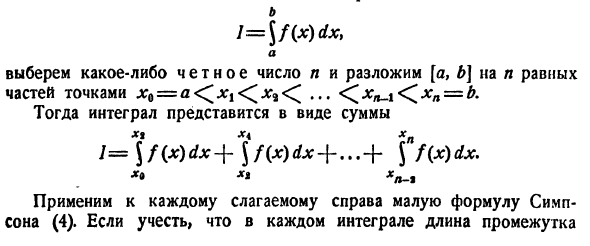




Приближенное вычисление определенных интегралов
Примерный расчет конкретного интеграла № 1. Постановка вопроса. Формула Ньютона – Лейбница сводит вычисление конкретного интеграла от функции к нахождению его обратной производной. Следовательно, если это последнее (т.е. обратная производная) не является элементарным, то должна быть рассчитана некоторая форма конкретного интегрирования. Иногда это можно сделать, минуя «обход неопределенных интегралов». *) Это ясно из соображений симметрии.
- Степень. На самом деле, форма такого многочлена / (X) = A ** + D * «+ C * + D Вам просто нужно убедиться, что формула относится к каждому термину. В качестве примера поясняется первый термин. Поскольку коэффициент A можно получить со знаком интеграла и круглыми скобками в правой части уравнения (4), проблема заключается в интеграле б B * -a * х * дх В этом интегрировании y = x * и, следовательно, ya = a \ yb = b *. также -1a + b \% __a ‘+ zdc + evil-b • y * — \ ~~ F ~ j-8 • Следовательно, правая часть уравнения (4) имеет следующий вид: бт т. , , B-o Za * + Za’b + W * 4-Zb * b * -o * -I I Vb) = -Q — 2- = -4 ‘ Это доказывает наше утверждение.
Пример. если 1 l = \ xidxt o Тогда y = x *, a = 0, b = 1, c = 0.5, почему Ya = 0Усyy = 0,0625, уу = 1 И уравнение (4) / = 0,208. (5) Фактически, поскольку / = 0,2, абсолютная ошибка (5) в уравнении равна 0,008, а относительная 0,04 = 4%.
Для более сложных функций уравнение (4) является лишь приближенным, но вывод показывает, что оно является точным, когда y = f (x) с небольшой кривой. Людмила Фирмаль
PM Представление объема тела с помощью уравнения Симпсона. Рассмотрим объект высотой L. Выровняйте дно (Рисунок 253). Fx указывает площадь поперечного сечения тела с горизонтальной плоскостью х расстояние от основания. Как известно [§ 3, формула (8) |, объем V нашего тела равен V = \ Fxdx. в Используя уравнение (4)
Более выразительная запись для этого выражения: V (т ниже + 4 ^ cp-f- ^ вершины) * Эта формула часто используется на практике (например, при расчете кубиков). Во многих случаях это совершенно точно. Например, для конусов или шаров уравнение (6) показывает точное значение объема *). Конечно, радиус мяча? L = 27? , -F top-O, F co-nR * брак Для конуса расчет аналогичен. n «5. Приближенная линеаризация эллипса. Это поднимает проблему выражения длины s эллипса. (7) (8) Через свою полуось а и б. Поскольку s не является основной функцией A & M, мы можем только сказать приблизительное выражение.
Существует много таких форматов, но угадывается только один из них. Для этого напишите эллиптическое параметрическое уравнение (7) x = a cos U Y = b sin t Для того чтобы точка (lx, yy) описала весь эллипс, необходимо изменить t от 0 до 2 mf в уравнении (8). Ограничить нахождение длины дуги эллипса по первому координатному углу. Эта дуга описывается точкой (dg, y), когда t изменяется от 0 до y. так «/» * / 9 i-s = ^ Vxi% + y’t% dt = 1§Ya% + & «* ‘tdt. (С) Дайте один ниже (6) Рисунок 253.
- Этот интеграл * •) не является элементарным (следовательно, s не является элементарной функцией от a и b). Применим уравнение (4). Где роль чисел а, б, в, Воспроизводя 0, ~ включенный в это уравнение, подынтегральное выражение r = Ya * sin ^ -f-A * cos4. *) Это результат того факта, что для конусов и шаров Fx является квадратичной функцией от x, а уравнение (4) верно даже для кубических полиномов (как показано на стр. 371). **) Из-за своего происхождения этот интеграл называется эллипсом.
так #M f ag + b Откуда И наконец (9) Чтобы достичь этого приближения, рассмотрим два частных случая, когда точное значение s известно. Во-первых, когда a = b, если эллипс уменьшается до круга с радиусом a, уравнение (9) возвращает точный результат s = 2na. Предположим, что k = 0. Затем эллипс вырождается в отрезок q отрезка Oq, который проходит дважды (чтобы лучше это понять, представьте себе очень маленький эллипс k> 0 (7)). Следовательно, точное значение s равно 4a. Уравнение (9) s ^ y (1 + 2/2). Если te = 3.1416 и / 2 = 1.4142, мы получим s ^ 4.0091l.
Таким образом, здесь абсолютная ошибка <0,01 °, а относительная ошибка <0,25%. № 6. Большая формула Симпсона. Малая формула Симпсона дает интеграл точно, когда граф подынтегрального выражения слегка изогнут. Наоборот, в этом случае Рисунок 254. Фига жена. 254, выражение явно неуместно, потому что оно дает нарисованную область 0. Однако когда сегмент [a, b] делится на части [a, c] Применение [c, b] и уравнения (4) к каждому дает приемлемые результаты.
Таким образом, здесь абсолютная ошибка <0,01 °, а относительная ошибка <0,25% Людмила Фирмаль
Эта идея лежит в основе заключения формулы .big Симпсона. Я хочу рассчитать интеграл б I = \ f (x) dx, Выберите четное n и разбейте [a, b] на n равных частей в точках x0 = a <q, <ng <… <^ xl_x <^ xn = b. Интеграция отображается в виде суммы Xt * 4 Xp l = \ f (x) dx + \ f (x) dx + … + \ f (x) dx Примените небольшое уравнение Симпсона (4) к каждому члену справа. Учитывая длину промежутка в каждой интеграции
Интеграция равна 2б-п (Есть сегменты [jcq, jc,], [xv jcj), … и интервал интегрирования вдвое больше), а f (xk) = yk, … + H5G + или / ^ 1Such + yi) +4 Cvi-f … + Yn-t) +2 SU, + yi + — .. + Yn- *)] • Для простоты Y + yn = y * p вичи — Бухгалтерский учет Найти в конце (10) дх ^ (ккр + 4 кнех + 2 кчет). Это замечательный рецепт Симпсона *. Его точность высока и l увеличивается. Качество этой формулы лучше, чем формула трапеции. Это связано с тем, что более высокая точность достигается при одинаковом n (то есть при одинаковых вычислительных затратах). Пример. Применить (10) к интеграции 1 D dx _ ) Т + П-4 ‘ о
Х у 0 я lU {J = 0,9412 V * 0,8 * А 0,64 1 0,5 y, r = 1,5, Kpe, -1,5812, K, «= 0,8, -K, p + 4 UVSCH + 2U» = 9,4248. Поэтому (после n-4) 5 * 4-9,4248 Можно видеть, что уравнение (10) предоставляет средство для точного вычисления важных констант, таких как mc (т. Е. Mc = 3.141592 …). Увеличение l увеличивает точность mc. Относительно Это просто «X sin x 1 + cos’jc Это не окончательная форма. Чтобы найти интеграл /, сделайте замену η = it-z. * х , P (i-z) sin g, C sin g dz. j = \ 1 + cos ‘* dz = «\ 1 -) — с06 * 2 смысл Х х n, f sin2Лfd (cosг),., Ч1Ж ** Я + ^ F ^ -JTT ^ = — * Нет. <cos = T ‘ Откуда / == ~ G ‘
Однако ясно, что здесь мы имеем дело с исключительным случаем. Вообще говоря, некоторые интегралы функций с неосновными антипроизводными должны быть вычислены с использованием того или иного приближенного выражения. Таких формул много, но только две из них представлены читателю: формулы трапеции и Симпсона. № 2. Трапециевидная формула. Дай мне б l = \ f (x) dx. Пример. Дай мне х х грех х , .__. дх. , 1 -j- cos «X о J L ^ ‘L dx
Где f (x) — непрерывная функция, и для ясности она считается положительной. Далее он представляет область изогнутой трапеции, окруженную линиями x = a, x = b, y = 0, y = f (x). Выберите положительное целое число n и используйте [x, x, x, <Xi <… … <xn = b, чтобы разложить [a, b \ на n равных сегментов. Линия x = xk дфелит трапецию целевой кривой на n полос.
Используйте каждую из этих полос для правильной прямой трапеции (Рисунок 251, где / 1 = 5). Далее область первой левой полосы представлена приблизительным числом -o \ xi —Xq) -— o— • —i-, H / в L Я 4 4 Рисунок 251.
Для нижней части трапеции, чтобы получить полосу, f (x0) = y0 и f (xl) = yx> и ее высота xx- = аналогично Кроме того, область полосы представлена числом. Таким образом, для интеграла вы получите формулу *) Для краткости L + .Y * = + + Yn-1 = Kprom, Наконец приобрел **) 0) Это приближение называется трапецией. Чем больше ги вы взяли, тем точнее вы можете видеть.
Найти 7 = ^ x * dx. (2) Точное значение этого интеграла легко найти: Однако, если он не может быть интегрирован, он «делает вид» и находит 7, используя формулу трапеции. Выбор числа n зависит от нас. Возьми n = 5. используя таблицу y = x \ a = 0, 6 = 1
Kkr = 0 + 1 = 1, Upr = = °> 04 + 16 + + OM = 1,2, Ukr + 2Kpr011 = 3,4. Следовательно, == ^ = 0.34. Поскольку точное значение интеграла составляет 0,3333 …, абсолютная ошибка составляет менее 0,007 и относительная Х у 0 0 0,2 0,04 0,4 0,16 0,6 0,36 0,8 0,64 1 1 *) Значок Y означает «экстремальный» и «средний». * •) Приведенное выше предположение / (*)> 0 не имеет значения.
Около 007 -Vr ~ = менее 0,021, то есть менее 2,1%. Со многими техническими проблемами Эта точность достаточна для точности. На практике, однако, точное значение интеграла неизвестно (поскольку нет оснований думать иначе). Как оценить точность, достигнутую с помощью уравнения (1)? Это обычно увеличивает n и пересчитывает интеграл. Если результаты в приемлемом диапазоне точности совпадают, это почти всегда указывает на то, что желаемая точность была достигнута.
Вернитесь к интегрированию (2) и рассчитайте для η = 10, используя уравнение (1). Ккр = 1, Кпром = 2,85, укр до б 2, упр * -6,7, / = § = 0,335. Сравните значения /, соответствующие / 1 = 5 и n = 10 / 5 = 0,340, / 10 = 0,335, Вы можете видеть, что это отличается на 0,005. Предполагая, что истинное значение интеграла, по крайней мере, приблизительно соответствует найденному числу (то есть, например, с использованием /=0.3), вы можете видеть, что относительная ошибка при замене / 5 на /, 0 может быть принята во внимание Равно — ^^ <0,02 = 2%. Если практический расчет, необходимый для нахождения интеграла (2), выполняется с точностью, допускающей аналогичные ошибки, то значение / found может быть удовлетворено. Конечно / значение / 10 = 0,335 в нашем случае точное значение / = -1 = 0,333 …, абсолютная ошибка <0,002, относительная ошибка <0,006 или <0,6%.
Если критично, рекомендуется выполнить еще одну административную проверку. Х у 0 0 0,1 0,01 0,2 0,04 0,3 0,09 0,4 0,16 0,5 0,25 0,6 0,36 0,7 0,49 0,8 0,64 0,9 0,81 1 1
Замечания. Более полным образом было доказано, что абсолютная ошибка в уравнении (1) не превышает: r (* — * *) ‘L \ 2n * • Где K — максимальное значение | f ‘(*) 1 в интервале [a, b]. № 3. Маленькая формула Симпсона. Интегрировать, если линия y = f (x) между x = a и x = b слегка изогнута l = \ f (x) dx
Он представлен очень простой формулой. Чтобы угадать это, как обычно, считайте f (x) положительным и ищите область изогнутой трапеции aABB (рисунок 252). Для этого разделим Сегмент la, b \ (c, f (c)) в точке C в половине точки c = Линия y = f (Касательная к xy связана с P, а B связана с Q, чтобы получить три прямые трапеции. aAPp, pPQq, qQBb. Рисунок 252.
Примерное выражение интереса Замена области изогнутой трапеции aAB на сумму площадей этих трех трапеций, , ^ aA + pP b-a, pP + gQ b-a qQ — \ — bB b-a / == 2 • 3 до T 2 3 ‘2’ 3 * Откуда / <^ Cp [a A + 2 (pP + q0) + bB]. (3) Теперь, aA = f (a) = ya, bB = f (b) = ytr Сегменты pP и qQ не являются ординатой точки на линии y = f (x). Это потому, что P и Q касаются, а не выше.
Однако сами эти сегменты не являются необходимыми, но их легко найти, поскольку центральная линия трапеции равна половине суммы ее основания. Таким образом, Следовательно, pP nO. = 2us «и выражение (3) принимает вид (4) Напомним, что уравнение (4) здесь называется малой формой. Симпсон мул. Удивительно, но вы можете видеть, что это выражение абсолютно неуловимо, когда (x) является четвертым или младшим полиномом.
Смотрите также:
| Геометрические приложения определенного интеграла | Определители 2-го порядка |
| Механические применения определенного интеграла | Определители 3-го порядка |

