Приближенное решение многопродуктовой транспортной задачи методом агрегирования
Нередко лицо, принимающее решение, удовлетворяют хорошие, хотя и субоптимальные решения сложных задач. Как правило, это происходит в тех случаях, когда отсутствуют программы, позволяющие проводить точную оптимизацию, или когда использование таких программ требует слишком больших затрат из-за циклического обращения к ним, или же когда нет возможности усовершенствовать основное программное обеспечение вследствие жестких ограничений на время ответа.
Одним из методов, позволяющих упростить решение задачи, является метод агрегирования, заключающийся в замене множества объектов (таких как переменные, узлы сети и т.п.) одним объектом. В этом случае сокращаются как время решения задачи, так и требуемая машинная память. Однако полученное решение, как правило, не является оптимальным.
Будем рассматривать многопродуктовую транспортную задачу с 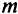 источниками,
источниками, 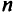 стоками и
стоками и 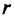 продуктами. Сведем ее к сетевой задаче с двумя источниками, разбив множество источников на два подмножества —
продуктами. Сведем ее к сетевой задаче с двумя источниками, разбив множество источников на два подмножества — 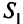 и
и 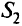 . Теперь необходимо определить новые предложения агрегированных узлов, решить вопрос о стоимостях и пропускных способностях агрегированных дуг и найти способ построения допустимого решения исходной задачи с помощью решения агрегированной задачи.
. Теперь необходимо определить новые предложения агрегированных узлов, решить вопрос о стоимостях и пропускных способностях агрегированных дуг и найти способ построения допустимого решения исходной задачи с помощью решения агрегированной задачи.
Поскольку каждый из двух агрегированных узлов представляет собой совокупность источников в исходной задаче, то величины предложения этих двух узлов 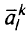 определяют как
определяют как
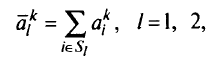
где 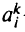 — предложение
— предложение 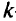 -го продукта из
-го продукта из 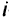 -го узла исходной задачи.
-го узла исходной задачи.
Пусть 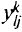 — поток
— поток 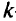 -го продукта из узла
-го продукта из узла 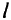 в узел
в узел 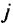 в агрегированной сети. Поскольку дуга
в агрегированной сети. Поскольку дуга 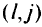 получена в результате агрегирования дуг, ведущих из узлов
получена в результате агрегирования дуг, ведущих из узлов 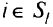 , в сток у, то
, в сток у, то
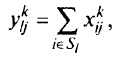
где 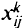 — поток
— поток 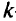 -го продукта из узла
-го продукта из узла 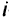 в узел
в узел 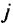 в исходной задаче.
в исходной задаче.
Для определения стоимостей воспользуемся понятием взвешенного агрегирования. Стоимости взвешивают пропорционально величинам предложения источников, представленных агрегированными узлами:
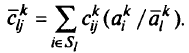
Для того, чтобы определить пропускные способности агрегированных дуг 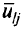 , найдем величины
, найдем величины
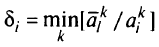
для
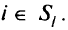
Тогда
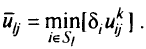
Если принять 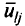 как сумму пропускных способностей исходных дуг
как сумму пропускных способностей исходных дуг 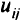 из источников
из источников 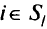 в сток
в сток 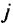 , то могут возникнуть трудности при построении допустимого решения исходной задачи.
, то могут возникнуть трудности при построении допустимого решения исходной задачи.
Сформулируем агрегированную задачу в виде следующей задачи линейного программирования:
минимизировать
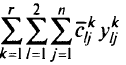
при условии,что
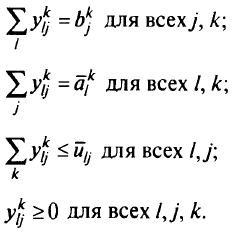
Теперь необходимо построить решение исходной задачи, использовав оптимальное решение агрегированной задачи. Определим величины
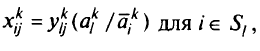
откуда следует, что
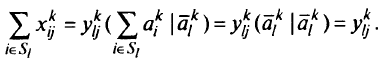
Эту процедуру называют дезагрегированием с фиксированными весами. Кроме того,
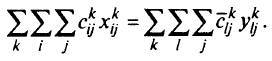
Иными словами, значение целевой функции в результате дезагрегирования с фиксированными весами не изменяется. Однако следует помнить, что в силу определения величин 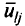 в агрегированной задаче может не существовать допустимого решения, лаже если в исходной задаче оно существует. В этом случае можно попытаться воспользоваться другими методами агрегирования.
в агрегированной задаче может не существовать допустимого решения, лаже если в исходной задаче оно существует. В этом случае можно попытаться воспользоваться другими методами агрегирования.
Продемонстрируем процедуру агрегирования на конкретном примере. Перейдем к решению задачи о транспортировке фруктов, сформулированной в разд. 5.3. Агрегируем источники 2 и 3. Величины предложения, стоимости и пропускные способности для агрегированной задачи содержатся в табл. 5.8.
Стоимость в оптимальном решении исходной задачи равна 18 570 долл. Стоимость в оптимальном решении агрегированной задачи равна 18 799,1 долл. и на 0,26% превосходит стоимость действительного оптимального решения.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
| Многопродуктовые потоки в сетях |
| Специальный класс целочисленных задач о многопродуктовом потоке |
| Приложения задач о многопродуктовом потоке |
| Эвристический алгоритм решения задачи синтеза сети связи |

