Оглавление:
















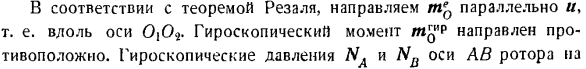





Приближенная теория гироскопа
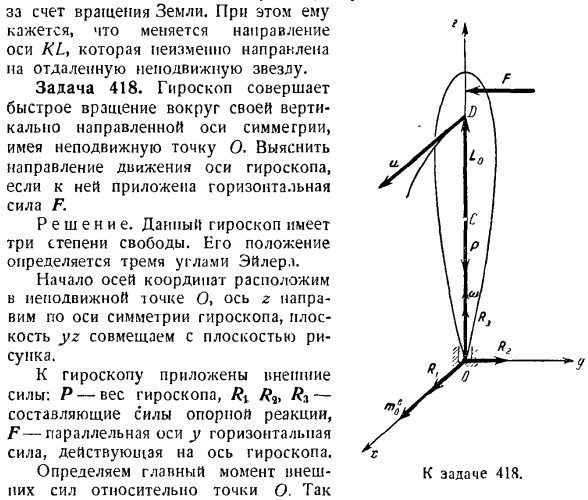
- Приближенная теория гироскопа 1°. 3 степени свободы гироскопа. Явление гироскопа наблюдается при быстром вращении твердого тела с изменением направления оси вращения. Гироскоп-это тяжелое твердое тело, имеющее ось симметрии и вращающееся вокруг точки На этой оси. Путем вращения Earth. At в то же время направление оси AX выглядит следующим образом changing. It всегда направлен к далекой звезде. Задача 418.Гироскоп имеет фиксированную точку O и быстро вращается вокруг вертикальной оси симметрии. Горизонтальная сила F. При добавлении гироскопа исследуется направление движения оси гироскопа. Решение.
Этот гироскоп имеет 3 степени свободы. Его положение определяется тремя углами Эйлера.1. Начало координат осей координат находится в неподвижной точке O, ось z ориентирована вдоль оси симметрии гироскопа, а плоскость yz совмещена с плоскостью рисунка. Внешняя сила приложена к гироскопу: P-вес гироскопа, Rv?9, R * — компонент силы реакции опоры, F-горизонтальная сила, параллельная оси y, действующая на ось гироскопа. Определяет главный момент внешней силы относительно точки O. сила относительно точки O так как моменты RX1 R9 и/ c3 равны нулю, то главный момент внешней силы относительно точки O вектор torio равен моменту силы F
Внешняя сила приложена к гироскопу Людмила Фирмаль
относительно точки O в направлении вдоль оси x (помните) момент силы относительно точки равен силе, направленной от края против часовой стрелки вокруг точки). Главный момент импульса гироскопа L0 в точке O примерно направлен вдоль оси симметрии к вектору угловой скорости. Конец вектора LQ обозначается буквой D. Применяя теорему резал Я=, скорость и точку D параллельно te0.Как результат, гироскоп оси симметрии отклоняется в узнать плоскость, то есть плоскость, перпендикулярную к направлению силы F.
При отсутствии вращения гироскопа, становится неустойчивое положение равновесия, и под действием силы Fego оси симметрии падает на плоскость YZ. Задача 419.После того, как симметричная ось гироскопа, изученная в предыдущем выпуске, была отклонена силой F, вес гироскопа P дает импульс относительно точки опоры O. если to-угловая скорость вращения вокруг оси симметрии, то 1-момент инерции гироскопа относительно оси симметрии, а если a-расстояние от центроида C до точки опоры O, то оно определяет движение оси гироскопа. Решение. ось xyz отображается в соответствии с положением осей на рисунке предыдущей задачи.
- К гироскопу прилагается внешняя сила. П является составной частью гироскопа и K » / 3-составляющая сила реакции опоры силу. 90. К (О. В Дж Р Момент власти и / или уважения?3 равно нулю, поэтому главный момент их внешней силы М-0 равен вектору. К задаче 419.Измерение веса P относительно точек O поддержка. Если угол между осью симметрии и осью z гироскопа равен 0, то можно увидеть следующее: / mp01 = па грех О, (я) Где вектор te0 направлен вдоль оси Y. Основной момент импульса L () гироскопа относительно точки O направлен вдоль оси симметрии к вектору угловой скорости o и имеет равное абсолютное значение. (2) | / .01=/ «、
Конец вектора LQ обозначается D. согласно теореме Резаля、 u = m ’ 0; следовательно, и-скорость точки D-направлена к вертикали К оси симметрии (параллельной оси y) и из Формулы (1)、 с — = ПА sin0.(3) Вес P в любом положении гироскопа создает момент t 0 0 для точки O. So,. Ось с определенной угловой скоростью U это движение называется регулярной прецессией оси гироскопа. И= AD Из треугольника ОАО, AD-OD sin 9 = L0 sin 9 является obtained.
точка D имеет постоянный коэффициент скорости и направлена перпендикулярно вертикальной плоскости, в которую входит ось симметрии гироскопа Людмила Фирмаль
By подставляя значение выражения (2)\ L0\, получаем: и = [шо1sin 0.(4 )) Вводя Формулу (4) в (3), мы видим угловую скорость регулярной прецессии оси гироскопа. Ра. Чем меньше скорость вращения гироскопа, w, тем больше угол его окружности.™ Скорость прецессии a ^(угол 0 не зависит от величины угла 0). Скорость u можно описать как векторное произведение 2 векторов, используя формулу v = o) X.
In в этом случае вектор радиуса r является главным моментом импульса гироскопа L0 относительно неподвижной точки O, а вектор угла Скорость-это вектор угловой скорости o) t precession. So … L0 = C0, so / / = ω, X / o по теореме Резаля, u = m » 0l. следовательно, главный момент внешнего Си. те0 = 1-х»>• В этот момент meQ стремится перевернуть ось симметрии гироскопа. 2°. 2 степени свободы gyroscope. To измените направление оси симметрии гироскопа
В случае свободы возникает пара сил, создающих дополнительную динамическую реакцию опоры. Момент пары дополнительных динамических осевых давлений для опоры называется моментом гироскопа (следовательно, момент гироскопа является моментом инерции гироскопа).Появление момента гироскопа называется эффектом гироскопа.
Задачи с использованием теории аппроксимации гироскопа рекомендуется решать в следующем порядке: 1) проверьте, имеет ли гироскоп или система гироскопа 2 степени свободы. 2) Выберите систему координат. 3) внешняя сила, приложенная к гироскопу, показана на рисунке. 4) определить основной момент импульса гироскопа LQ Относительно неподвижная точка; 5) найти скорость и конец L0. 6) примените теорему Резаля и= mc0>для определения главного момента Дополнительные динамические силы реакции внешних сил и опоры для неподвижных точек.
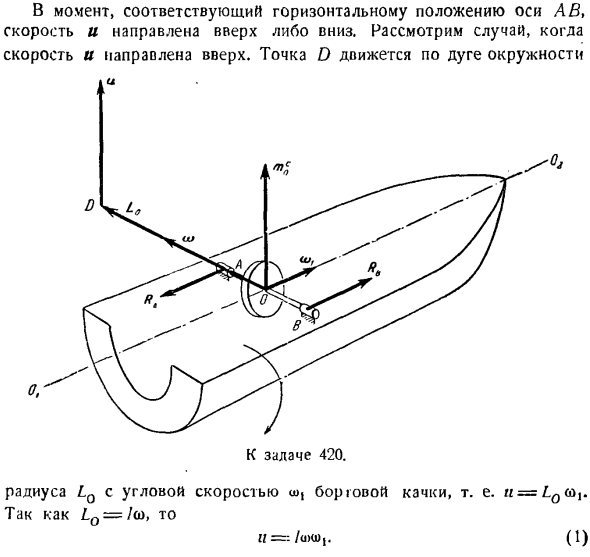
Задача 420.Ротор электродвигателя, соединенный с компрессором, установленным в судне, имеет горизонтальную поворотную ось AB. Ось A B перпендикулярна продольной оси судна 0.02.Оси A B и 0.0-2 пересекаются в центре масс Ротора O. момент инерции ротора к оси AB равен/, o).Угол поворота ротора. При установившемся качении судна, происходящем вокруг оси 0, ОО определяет максимальное значение дополнительных динамических сил реакции опор а и В.
гармонический закон судна вокруг оси OtOq воспользуемся соответствующим уравнением движения o,= sr0 sin y t -. — футы — потому T T и(0 |ШХ. Где выражение (I) принимает вид: ’»=(2) Применяя теорему Rszal u = te0, мы направляем основные моменты внешних сил параллельно, то есть в вертикальном направлении вверх. Рассматривая Формулу(2), можно увидеть: М <0 = ^ / Вт. (3) Во-первых, рассмотрим случай, когда гироскоп движется вблизи неподвижной точки. Если вы выберете начало координат в этой точке O и направите ось z вдоль оси симметрии гироскопа, оси x,
y и z станут главной осью инерции гироскопа в неподвижной точке(рис.158). Mo- Момент инерции/, является полярным моментом инерции гироскопа,\ x и/,. — Момент инерции экватора. Поскольку твердое тело имеет ось симметрии, оно будет 1x = 1y. так симметрично Sntrffl? Вращайте гироскоп с угловой скоростью (O) вокруг оси симметрии, а ось симметрии вращается вокруг неподвижной точки (рис.159) с угловой скоростью (u).Согласно теореме о сложении вращения твердого тела вокруг пересекающейся оси, абсолютная угловая скорость
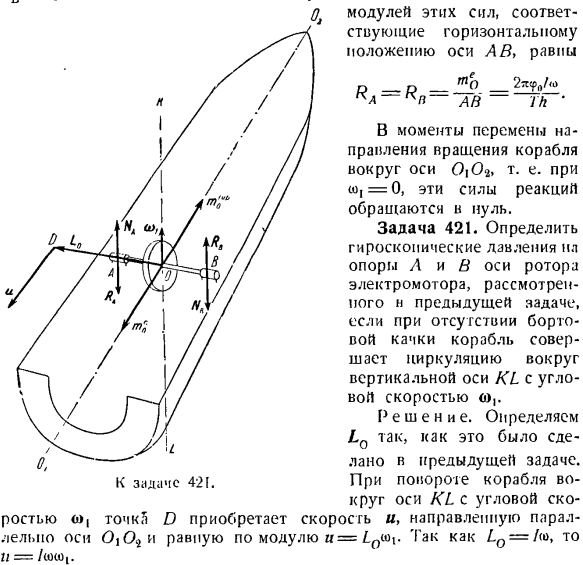
Коэффициент этих сил, соответствующий горизонтальному положению оси а Д-д-Улс} 2 * jppA» — влево. В момент изменения направления вращения корабля вокруг оси 0.0*, то есть при ω= 0, Эти силы реакции исчезнут. Задача 421. Опорное гироскопическое давление Li определяет угловую скорость судна (II, когда нет тряски. Решение. \ г ^ ^! Определить / \ Ln как есть От-Лано предыдущей задачи. К задаче 421.Когда корабль поворачивает Окружность оси KL угловой скорости oj, точка D, параллельна оси 0.04 и приобретает скорость u, величина которой равна u = 10sh. У = /(0(0,.
В соответствии с теоремой Резаля, мы направляем te 0 параллельно if, то есть вдоль оси 0 \ 0$.Гироскопический момент p имеет противоположное направление. Гироскоп давление N и Al ось AB Ротор включен Опоры А и в находятся на вертикальной плоскости, образуя пару forces. It виден против часовой стрелки от конца пара. u = / u ,, и| mffp \ = = \ meQ \ = \ u \ t потому что um™p = / > > становится w1 и, следовательно, желаемое давление / OJWj — 1г АС
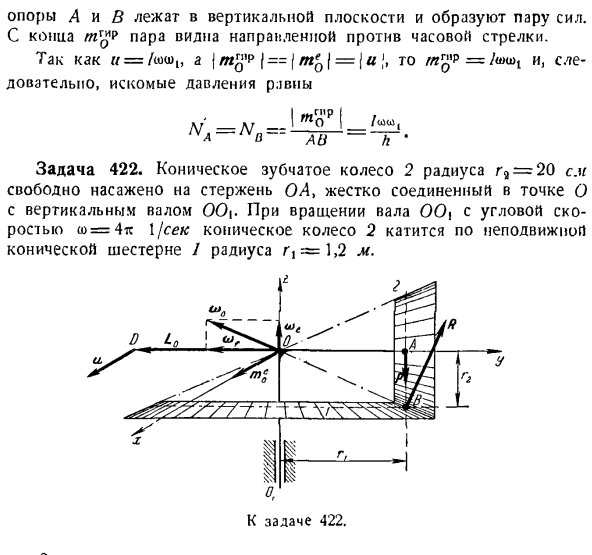
Задача 422.Свободно установленный радиус= 20 см коническая шестерня 2 на валу OA. At точка O прочно соединена с вертикальным валом 00.Радиус R | = 1,2 м К выпуску 422. Если радиус инерции колеса 2 равен Р = 18 см, то определяют отношение дополнительной динамической силы реакции шестерни Y к статической силе реакции, игнорируя массу вала ОА.
Для определения места расположения религиозного колеса 2 достаточно задать 2 независимых параметра: угол поворота вала ОА вокруг вертикальной оси и угол поворота колеса 2 вокруг вала ОА. Таким образом, коническая шестерня 2 является гироскопом 2-DOF. Ось симметрии гироскопа совпадает с осью стержня ОА. 2 пересекающиеся оси OA и 2 шестерни, участвующие во вращении вокруг OOt, вращаются вокруг неподвижной точки O. направление осей xyz показано на рисунке. Bcc колесо 2 обозначается буквой R.
Внешняя сила приложена к лесу 2.P-вес колес, Rt, P.、, — сила реакции шарнира О (эти силы не показаны на рисунке), а нормальная сила реакции R направлена перпендикулярно оси OB. Определите статическую реакцию поддержки Rcx. Для этого учтем равновесие шестерни 2 и создадим уравнение момента для точки О. RCT * OB-P-OA = O、 Где его найти: При изменении направления OD оси колеса 2 отображается дополнительная динамическая опорная реакция R.
Определите заранее скорость вращения колеса 2 вокруг оси ОА. Колесо 2 совершает переносное вращение вокруг вертикальной оси с определенной угловой скоростью ^ = o> = 1 jceK> p = 18 sll, r * = 20 sll:-.- ^- ^2 6.Следовательно, динамические реакции т. Поведение колеса 2 при движении колеса 1 в 3,6 раза превышает силу реакции в соответствующем состоянии покоя. Дополнительный момент te0>модуль определения уравнения(3) равен、 Уравнения Эйлера (см. задачу 427 ниже).
Когда гироскоп вращается с большой относительной угловой скоростью o, а ось симметрии гироскопа z изменяется медленно Положение (то есть ориентированное вдоль оси симметрии с\ L0 \ = / / o).На этом предположении основана приближенная (базовая) теория гироскопов. Рассмотрим случай, когда все точки оси симметрии гироскопа находятся в движении. Разлагает абсолютное движение гироскопа на поступательные движения, которые инерционны и относительно центра вращения, но относительно центра inertia.
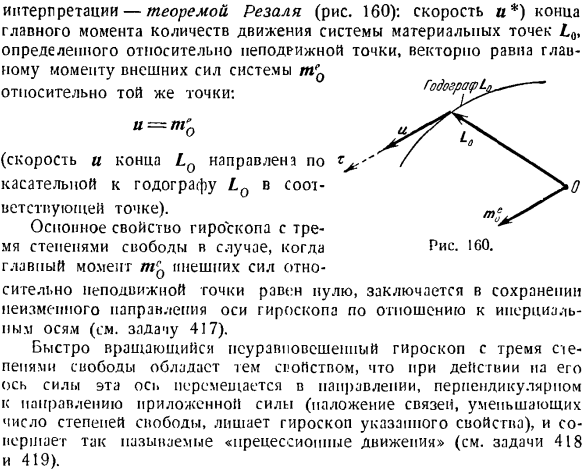
In в этом случае основной момент импульса гироскопа относительно центра инерции гироскопа также направлен почти к оси симметрии, и величина его равна r <0. При решении задачи с использованием теории гироскопического приближения удобно использовать теорему об изменении основного момента импульса системы дшериальных точек в ее кинематике. Рисунок 150. Интерпретация-теорема Резаля (рис. 160): скорость окончания главного момента импульса системы материальной точки£0, определенной по отношению к неподвижной точке a*, равна главному моменту внешней силы системы π0,
связанной с этой же точкой.: у = Т Да. (Скорость и конец LQ направлены тангенциально к LQ-годографу в соответствующей точке.) Основные характеристики гироскопа с 3 степенями свободы в корпусе 160.Основной момент внешней силы относительно неподвижной точки, mc0, равен нулю, что заключается в поддержании того же направления оси гироскопа относительно вертикальной оси (см. задачу 417). Быстро вращающийся
несбалансированный гироскоп с тремя степенями свободы под действием своей оси силы имеет свойство своей оси двигаться в направлении, перпендикулярном приложенной силе (это свойство снимается с гироскопа наложением муфты для уменьшения числа степеней свободы) (см. задачи 418 и 419). Ход граф L Рекомендуется решать задачу определения движения оси гироскопа, используя теорию аппроксимации в следующем порядке: I) проверьте, имеет ли гироскоп или система гироскопа 3 степени свободы. 2) Выберите систему координат. 3) внешняя сила, приложенная к гироскопу,
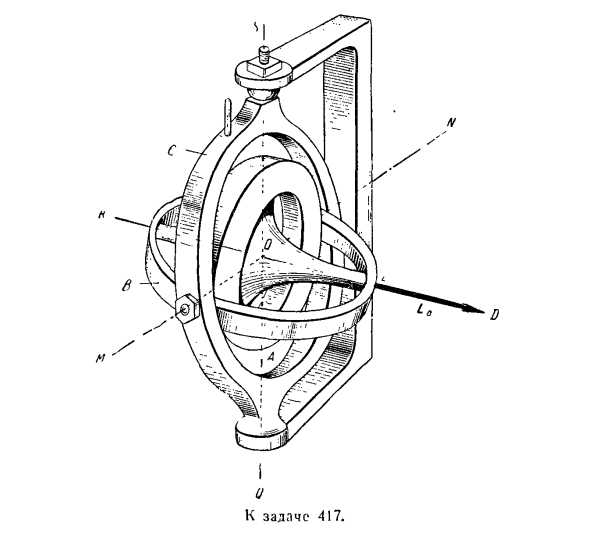
показана на рисунке. 4) Определите главный момент внешней силы Теа относительно неподвижной точки. 5) paygi-основной момент импульса гироскопа против неподвижности точки LQ. 6) Используйте теорему Резаля u = m для определения движения оси гироскопа. Задача 417.На этом рисунке показан гироскоп в карданном подвесе. Гироскоп а выполнен в виде сбалансированного гигантского цилиндра, вращающегося вокруг оси КЛ. Оси армирования КЛ * ) Из-за отсутствия размерности скорости вектор сразу же называется
произвольным. Во внутреннем кольце B он вращается вокруг подвижной оси MN. Ось MN закреплена на наружном кольце C, чтобы вращаться вокруг неподвижной оси sq. Ось SQ прикреплена к стойке оборудования. Оси KL, MN и SQ пересекаются в центре тяжести гироскопа. Гироскоп это будет большой угловой скоростью вокруг оси-оси. Определить изменение положения оси KLy, игнорируя трение подшипника и массу колец B и C осей D7, MN, SQ. Решение. Гироскоп 4 подвески Kalap имеет 3 степени свободы, поскольку его положение определяется 3 независимыми углами поворота вокруг осей KL>
MN и SQ, которые пересекаются в центре центра тяжести O. Поэтому гироскоп вращается вокруг неподвижной точки O, которая совпадает с центром тяжести. В этих условиях основной момент внешней силы относительно центра тяжести гироскопа равен нулю. t’O =0.(1) Основной момент импульса гироскопа LQ находится почти вдоль оси KL. Конец вектора LQ обозначается буквой D (см. Рисунок).
Если применить теорему Резаля u = tv по формуле (I), то u = 0, то есть скорость точки D равна нулю. Это означает, что при вращении гироскопа ось KL сохраняет постоянное направление в пространстве. Это свойство может быть использовано для доказательства вращения Земли (эксперименты Фуко).Действительно, наблюдатели на Земле обратятся к звездам
Смотрите также:
Предмет теоретическая механика

