Оглавление:

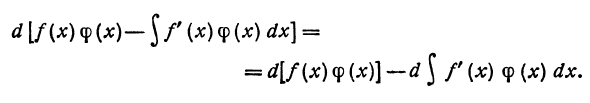

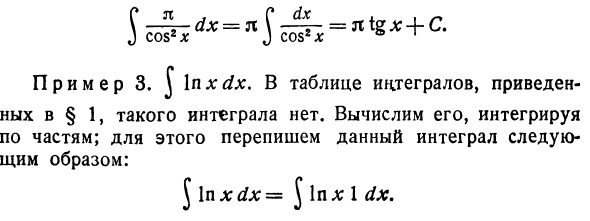

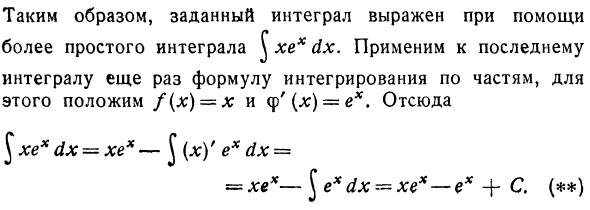
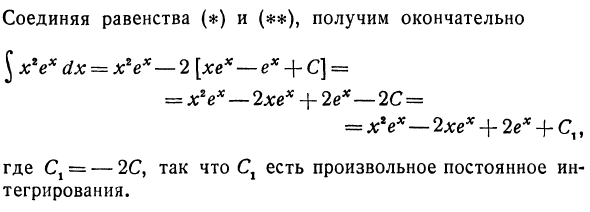

Преобразования неопределенных интегралов
- Преобразовать неопределенный интеграл Так же, как даны правила для алгебры, которые могут быть преобразованы для упрощения алгебраического представления, неопределенные интегралы имеют правила, которые могут преобразовать его. I. Интеграл алгебраической суммы функции независимо равен алгебраической сумме интегралов каждого члена. J [/ () + Φ ()] dx = J / (x) dx + JΦ (x) dx.
(1) II. (С является постоянным значением). (Ii) III. Формула интеграции детали, то есть: J / () Φ ‘(x) dx = f (x) q> () — $ /’ (x) Φ (x) dx. (III), Докажем уравнение (111). Получить производную от правой части уравнения (111) * 1 / () φ () — $ Л ) Ф () </ *]. Глава Примените Уравнение 4 из таблицы в 2. IX, мы получаем = </ [/ () Φ (x)] — d J / ‘(x) φ () dx.
Постоянные коэффициенты могут быть взяты из интегрирующего символа. Людмила Фирмаль
Термин ^ [/ (l;) φ ()] переводится уравнением 5 в той же таблице. d [f (x) Φ ()] = f (x) ρρ () + φ (x) d / (x) = = f (x) v ‘(x) dx + v (x) f (x) dx9 И член d J / ‘(x) Φ () dx в соответствии с уравнением (B) в § 1 этой главы d J / ‘(x) (f (x) dx = f’ (x) φ (x) dx. Собираем все вместе, </ [/ () Φ () — $ / ‘() Ф (x) dx] = = f (x) φ ‘() dx + Φ () /’ () dx-f (x) φ (x) dx = = / (*) Φ ‘(Л 🙂 dx, Другими словами, мы получили то, что получается путем дифференцирования левой части уравнения (III). Уравнения (I) и (II) проверяются аналогичным образом.
Пример 1. ^ (xx-sinx) dx. Применяя правило интеграции I и уравнения 1 и 5 из таблицы интеграции: ^ (L; 1-sinx) dx = ^ xg dx — J sin xdx = х * х% = j — (- cos l 🙂 + C = y + cos x + C Пример 2. \ «dx. Использование правила II и выражения J cos x 6 Из таблицы интеграции Пример 3. j Inldgdx. Нет такой интеграции в таблице интеграции, показанной в §1. Рассчитать путем интеграции в части. Поэтому перепишите этот интеграл как J In xdx = J In l: 1 dx.
- Если / (η) = 1πl и <p ‘(ds) = k1, применяется правило интегрирования для каждой части. J In xdx * = In l: f (l:) — J (In x) ‘f (l;) dx. Однако <p (x) = ^ φ ‘(*) dx = J 1 • dx = J x ° dx, поэтому, используя уравнение 1 (η = 0) в таблице интегрирования, получим Φ = π вы. наконец ^ lnxdx = x In l: -§ ± xdx = = l; 1n x-J dx = x In x — x + C
Пример 4. Рассмотрим ^ xs \ nxdx. Когда вы применяете пошаговую интеграцию, ^ x sin x dx = -x cos x-J (x) ‘(-cos x) dx = = -x cos x + j * cos x dx = -x cos x + sin x + C Пример 5. Рассмотрим ^ x * exdx. Положите f (x) = x% и (f ‘(x) = ex. Тогда <p (x) = ex, (ex)’ = ex. Используя интеграцию деталей, J x * ex dx = xhex-J (l: 1) ‘e * ^ l: = = xV — 2 ^ xe * dx. (*)
Положите f (x) = x И f ′ (l 🙂 = грех х. Далее φ (π) = — cosx, (−cos *) ′ = sin ;; Людмила Фирмаль
Следовательно, данный интеграл Упрощенная интеграция Jхехdx. Применимо к последнему Интегрировать часть интеграла снова. Для этого положим f (x) = x и cp ‘(x;) = ex. Отсюда £ хе дх = хе — ^ (l 🙂 ‘ex dx = = xex— [exdx ^ xex-ex + C. (**) Объединение уравнений () и (*) ^ l; V dx = x * ex-2 [heh-e * + C] = = JcV- + 2e * —2C = = -2hex + 2ex + C ,, Где C = -2C, поэтому Cj — произвольная постоянная интегрирования.
Смотрите также:
| Применение дифференциала к различным задачам | Замена переменного интегрирования (метод подстановки) |
| Первообразная и неопределенный интеграл | Приближенное вычисление площадей криволинейных трапеций |

