Преобразование системы сил. Условия равновесия

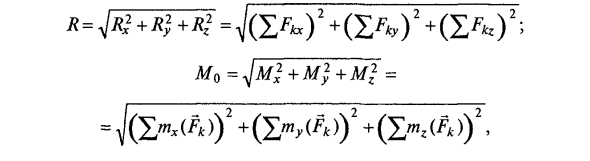
Преобразование системы сил. Условия равновесия

• Преобразование энергосистемы. Состояние равновесия Обычно на тело или механизм воздействует система сил, произвольно размещенная в пространстве. Сходящаяся система сил может быть заменена результатом, приложенным на пересечении силовых силовых линий. Мы подводим любую энергетическую систему к определенной точке тела. Сила F, приложенная к точке A, применяется к телу, но она должна передаваться параллельно точке O (рис. 3.4, а).

Получает систему сил, соответствующую силе F, состоящую из пары сил F ‘-F и пары моментов = mo (F) = Fh. Где h плечо силы F против точки восстановления. Пара сил характеризуется плоскостью действия и величиной и направлением момента пары. Все это можно выразить как моментный момент пары сил m0 (P).

Чтобы получить эквивалентную систему, примените уравновешенные силы F ‘и F в точке O «F-F \ a F’ = -F». Людмила Фирмаль

Абсолютное значение представляет собой момент пары, ориентированной перпендикулярно рабочей поверхности пары, и если смотреть с конца вектора, пара сил стремится повернуть тело относительно направления движения по часовой стрелке.Рисунок 3.4 Теперь рассмотрим тело, на котором действует произвольная система сил F {, F2, …, Fn (рис. 3.4, б). С любой точкой C в качестве центра замедления перенесите всю мощность системы в этот центр и добавьте соответствующую пару.

Тело тогда имеет систему сил сходимости f1 / V, приложенных к центру O, и пару сил, векторы моментов которых равны mj = m0 (Fi), m2 = m0 (/ r2), = m0 (Fn) Это зависит от системы. N Сила, приложенная в точке O, заменяется одной силой R =] ГFk. к = 1 Чтобы добавить все полученные пары, вы должны добавить геометрически! Вектор моментов для этих пар. В результате паровая система заменяется одной n __ Силовая пара M0 = ^ u (Pk). Поэтому система питания. * = 1

• При воздействии на твердое тело и приведении к произвольному центру O заменяется основным вектором системы, приложенным к одной точке R силы O, основным системным моментом системы для одной пары M0-центр O , Векторные модули R и Mo имеют координатные оси (рис. 3.4, б): R = + Ry + x * = + (XM ‘+ (5L)’ 5 Mn = ^ / l / i + M] + l / r2 = = J (5> X (A)) 2 + (2>, ) 2+ (5> << A)) 2,

-Момент силы Fk относительно осей ОХ, ОГ, OZ. В следующих случаях тело под воздействием силовой системы будет отдыхать. R = ± Fk -0; A / 0 = £ m0 (^) = 0, (3.3) к = 1 Или проекция на координатную ось (формат анализа): Yah = = 0; Ry = J ^ Ffy = 0; Rz = ^ = 0; Mx = Yjnx (Fk) \ My = Jmy (Fk) \ Mz = ^ mz (Fk). (3.4) Такая система сил считается равновесной. Для баланса любой системы сил необходимо и достаточно, чтобы сумма всех проекций сил на осях и сумма всех моментов сил на осях были равны нулю.

Где Ffr, Fty и Fkz — проекции силы Fk на оси координат OX, OY и OZ соответственно. mx (Fk)} my (Fk) y mz (Fk) Людмила Фирмаль

В зависимости от системы сил, действующих на тело, число уравнений равновесия уменьшается. Например, объект, на который действует система сил в плоскости OXY (плоская), находится в равновесии при следующих условиях: Rx = = 0; Ry = Mz = lrnz (Fk). (3.5) Уравнения (3.3) — (3.5) устанавливают состояние равновесия свободного тела, на которое воздействуют различные силовые системы. Если тело не является свободным, то есть к нему добавляются связи, и помимо внешних сил силы реакции связывания находятся в равновесии.

Смотрите также:

Предмет прикладная механика

Задачи динамики механизмов	Силы трения
Силы, действующие в механизмах	Силы инерции звеньев