Оглавление:

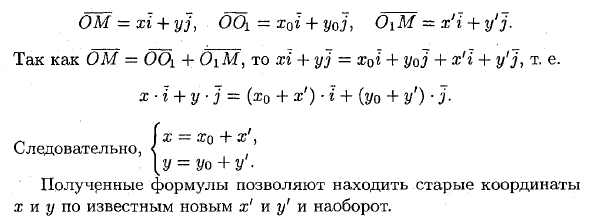


Преобразование системы координат
- Преобразование системы координат Переход из одной системы координат в другую называется преобразованием системы координат. Рассмотрим два случая преобразования одной декартовой системы координат в другую. Полученная формула устанавливает связь между координатами любой точки на плоскости в разных системах координат. 1. Перевод координатных осей Дайте декартову систему координат Ohu на плоскости.
Эта система изменяет положение начала координат и не меняет направление оси и масштаб. Y 1 | M /// 1 год \ 1 / • я / ^^ Си V \ \ / / 1 я! О х х Пусть источником новой системы координат является точка 0 \ с координатами старой системы координат Oxy (* r0; y0), то есть Oi (xo ;? / O). ♦ Координаты произвольной точки M на плоскости системы Oxy (x) y) и 0 \ X \ y \ through (.x ‘\ y’) в новой системе.
Параллельная передача осей координат означает переход от системы координат Oxy к новой системе OiX \ y . Людмила Фирмаль
Думаю вектор OM = xi + y], OOi = x0i + yoj, 0 \ M = x’i + y’j. Так как OM = OOi +, xi -f yj = + yoj + x’i + y’j, то есть x • t + y •] = (i0 + • * + (y0 + y ‘) • j. = aro + x ‘, Y = yo + y’. Полученная формула может найти старые координаты x и y из известных новых x ‘и y’ и наоборот. так
Координата оси вращения Вращение оси координат означает преобразование координат, при котором обе оси вращаются под одним углом, а начало координат и масштаб не изменяются. Поверните систему Ohu на угол a и получите новую систему 0 \ Xiyi. Пусть M — любая точка на плоскости, (x; y) — координаты старой системы, (x ‘\ y’) — координаты новой системы. Вводит две полярные системы координат с общим полюсом O и полярными осями Ox и Ox 1 (в одном масштабе).
| Система координат на плоскости | Уравнение линии на плоскости, примеры |
| Основные задачи на метод координат (на плоскости) | Различные виды уравнений прямой на плоскости |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Полярный радиус r одинаков для обеих систем, а полярный угол равен 4-y3 и tp> соответственно. Где tp — полярный угол новой полярной системы. Согласно формуле перехода от полярных координат к декартовым x = r • cos (a: -f tp), y = r sin (a + tp). x = r cos tp • cos a-r sin tp • sma, y = t cos tp • sin a -f r sin tp ■ cos a. т. Ho r cos tp = x1 и r sin tp = y ‘. так x = x ‘cos a-y’ sin a, y = x ‘sin a + y’ cos a
Полученное выражение называется типом вращения вала. Их можно использовать для определения старых координат (i; y) любой точки M из новых координат (x ‘\ y’) той же точки M или наоборот. Если новая система координат 0 \ X \ y \ получена из старого Ohu путем перевода оси координат с последующим поворотом оси на угол a, то формулу можно легко получить, введя вспомогательную систему 0 \ xy x = x ‘• cos a-y’ • sin a 4-xo y = ■ x ‘• sin a + y’ • cos a + yo>
Выразите старые координаты x в y любой точки с новыми координатами x ‘и y’. Людмила Фирмаль

