Оглавление:








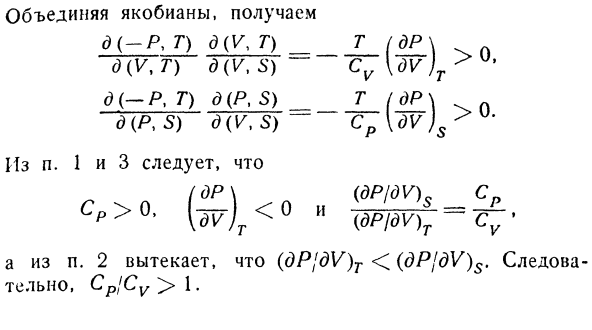

Преобразование переменных.Применение детерминантов якоби
- Преобразование переменных Рассматривается общий метод преобразования переменных в термодинамические уравнения. Получены соотношение Максвелла и термодинамическое уравнение состояния.Рассматривается проблема излучения черного тела.
Получено изоэнтропийное отношение.Определена параметрическая инвариантность. Используя детерминант Якобиана В термодинамике существует так много отношений между различными частными производными, что нет смысла вспоминать them.It лучше запомнить только термодинамическое тождество (4.3), определение термодинамического потенциала (4.4) и некоторые правила преобразования множества переменных в другое множество.
Одним из них является компиляция якобианского определителя Людмила Фирмаль
Используются следующие 2 свойства Якобиана являются : 1.Если _d(ХL%Х2,..хр) d (y)~ ~ ~ d(y » > ’ 2, одно предприятие)’ d (y) d (ylt y2,.вверх.) Д (Г) Д (Г1%Г2 ….. врач общей практики’ ) Является переменной x = xv x2, соответственно…Множество y = = = yv преобразование в y2, а определитель функции преобразования y в множество r = zv z2f.) имеем Д(х)d(ХХ … хы) Д(х)Д (Г), 9 д(р)0(р,… Ж) 0 (У) 0 (р)’ Х — > г、 (5.1)) Г — > З
Это… 、 д (д)}.к ДЗК ДЗК 2Д-Зи \ Д (Г))и д (р)) в JK ’ (5.4) (5.3) Поэтому Якобиан обладает свойствами, которые можно разделить на любой метод. Д(х)= Д (х)Д (Г)Д(х)Д(А)Д (Я) ’ 2. 2-я характеристика заключается в том, что частичная производная может быть формально описана как Якобиан следующим образом: ки / д / Есть много других способов, но в самом общем случае достаточно воспользоваться вышеперечисленным methods.It показан только типичный пример его применения.
- Давайте узнаем адиабатический фактор. (5.6) Необходимо рассчитать соответствующий изотермический коэффициент, используя метод, описанный выше (дю \ Это можно сделать следующим образом: _d(г,Ы) _d (Г % С)Д(К,т) д (Х9 т)-д(Х, З)Д (Г,Т) Д (х, т) д (ХН Ы) (\ДС(ДТ \ ас = — ^ ч- — \ ДТ с)м \ ОС)Х ’ Поскольку величина T (dSfdT)имеет удельную теплоемкость, ее можно описать следующим образом: И Т = МБФ Вт
И например[ср. (1.36)]、 ДВ)Т-ЦВД (5.9) Таска. dU * dS2 [dVOS J Т._ С. т. a. используйте это соотношение, чтобы доказать, что коэффициент адиабатического сжатия больше, чем изотермический коэффициент. c. почему вода всегда больше, чем Су? (Среди задач, предложенных на экзамене Оксфордского университета 1962 года) Решение a. выражение слева является Якобианским. D(ди / ду,Ди / / ДС)_ д (- Пт, Т)Д(Г,х) — Д(Г, Ы))• Переписать в форму Д(Р,Т)Д (Г, Т) О (Г,Т)Д(Г,Ы)- Т. И в. т. И мы это доказали д * у d2U(d2U \ 2 _ т / д \ OV2 ОС2 [dSdVj-ЧВ \ DV)Т * a.
To докажите утверждение, сформулированное в условиях задачи, коэффициент изотермического сжатия-(dP!Сравните DV) T и изоэнтропический коэффициент — (dP / dV) s.я заметил. d2U _ ДТ _ Т ОС2 ~~ ДС-ЧВ И затем Д * С (Д-р \ дв> — \ ДВ) с ’ Из уравнения, приведенного в задаче » а»、 ІТ(р \ (dT_ \ 2 _ _ т (д-р \ ЧВ \ дв)з \ дв)$ — ЧВ [дв)/ С каких пор? После того, как вы установили (dPjdV) T <0, вы можете легко переписать выражение (1.22) в следующем виде:
Для стабильного состояния оба (dP / dV) Sl и (dPfdV) T отрицательны, поэтому наклон изоляции больше, чем наклон изотермы через ту же точку. Людмила Фирмаль
Теперь, когда мы преобразуем правую сторону, мы сначала используем отношение (2.72), затем мы используем отношение / др \ _ / dR (дв \ г-Uvjr \ ДТ)Р; Он становится < Cp> Su. Вот еще одно доказательство, но оно кажется более прямым. 1.Условия стабильности (см. Главу 3,§ 6)、 ^ х / ^ Т / Х — * а (ДП \&4 С а КР = МН) «[ДВ)с == — Мас <°- 2.НАУ из решения задачи мы знаем, что dVJr [dVJs Т \ ДВ)с ’ 3.Требования к стабильности ОВ * DS2 у [dVdSj> Его можно переписать как д(jdU / ду,ду / ДС)d (П. т)д [В % С)Д (В, С) Когда мы объединяем Якобианов、 Д (- П, Т) Д (Г, Т) — Т (ДП \ д(В,т)д(В,С) — резюме \ DV)Т ^ кДж ’ д (- п,т)д(п. С) Т (ДП \ п D (P, S)D (V, S) CpU ^ Js ^ Из пунктов 1 и 3、 dp_ (dP / 0V)s_ вода СР> 0, (£)<0,и J ^ вай — ^ с Из части 2, то он будет © PjdV) Т <(dPjdV) С. Поэтому, CpjCv> 1.
Смотрите также:
| Термодинамические потенциалы. Максимальная работа. | Преобразования Лежандра |
| Уравнения гиббса — гельмгольца | Примеры |

