Оглавление:



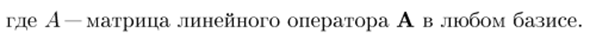

Преобразование матрицы линейного оператора при переходе к новому базису
- Преобразовать матрицу линейных операторов Переход на новый фундамент. Пусть Y линейное пространство, A a L (V, V), ei, b2, …, линейные операторы из en и ei, b2, …, en являются двумя основными С вашей SA N ek = ^ 2 и hk и k = 1, 2, …, n E.16) -Выражение перехода от базы {e ^} к базе {e /,}. Дисплей с U Матрица (ИГК): U = D). E.17) Обратите внимание, что rangt / = n. A = D) и A = (a {) E.18)
- Матрица оператора A в указанном базисе. Найти связь между По этим матрицам. Следующее предложение верно. Теорема 5.7. Матрицы A и A оператора A с базисом {ek} и {ek} Соответственно, связанный A = U-1 AU, Где U ~ l обратная матрица 6) определенная матрица U E.17). Доказательство.
Посмотрите на концепцию линейных матриц Получено по данным оператора, E.18) н н Aek = ^ 2agkeys Aek = ^ agkyo {. Е.19) г = 1 г = 1 Людмила Фирмаль
Из определения линейного оператора, выражения E.16) и второго выражения Уравнение E.19) означает отношение Ayok = A 1 ^ 2 Улей, Ayok = \ г = 1 / г Поэтому равенство Подставьте выражение слева от этого уравнения Найти вой из формулы E.19) нет {ej} является фундаментальным, поэтому из последних отношений: состояние н н ^ 2 и \ a {= ^ 2 <& {, h k = 1, 2, …, пункт E.20) г = 1 г = 1 (См. Матрицы A, A и U (E.17) и E.18))) Соотношение E.20) эквивалентно эквивалентности следующей матрицы: И А = Ау.
Умножение матрицы Ur с обеих сторон этого уравнения слева дает Требуемое соотношение составляет A = U ~ 1AU. Теорема доказана. 6) Поскольку звено U = m, существует обратная матрица U x матрицы U. Примечания 1. Используйте формулу от A = U до 1AU. умножение Обе стороны этой матрицы равны левой и правой сторонам матрицы U Получить отношения с U ~ 1 A = UAU’1, E.21) Представляет различные формы связи между матрицами A и A Другой базовый линейный оператор А. Замечание 2.
- Пусть A и B — квадратные матрицы порядка n, A и B — линейные операторы, соответствующие им в данном базисе {e &}. Как уже упоминалось (см. Примечание 3 в предыдущем абзаце), матрица A + XB соответствует линейному оператору A + AB. Уточнить форму матрицы Основа этого оператора {e &}. Пусть A и B — матрица операторов A И {йок} на основе Б. Далее по E.21) A = UAU ~ \ B = UBU-1 E.22).
Матрица линейного оператора A + AB базиса {ek} имеет вид Согласно E.21), следующий формат: U (A + XB) U ~ 1. Используйте дистрибьютора Фактическое свойство умножения матриц переписывает последнее выражение (Эта формула Матрица линейных операторов A + AB с базисом {e /,}: UAU-1 + i1) Глядя на отношение E.22), матрица Ра A + AB базиса {e /,} описывается следующим образом: A + XB.
В частности, если B — единичная матрица B = /, то B = / Людмила Фирмаль
Примечание 2 и теорему 5.5 в предыдущем абзаце) Матричная форма линейного оператора A + AI для базиса {e /,} есть A + XI. Результат теоремы 5.7. detA = det A Фактически, детерминант матричного произведения Вена на произведение определителей этих матриц, тогда уравнение A = = U ~ 1AU detA = detCZ-Metidett /. E.23) detU ~ 1detU = 1, то есть из E.23) det det A = detA.
Следовательно, определитель матрицы является линейным. Операторы не зависят от выбора базы. Таким образом, вы можете ввести Определитель det A понятие линейного оператора A, настройка detA = deti, E.24) Где A — матрица произвольных базовых линейных операторов A.
Смотрите также:

