Оглавление:

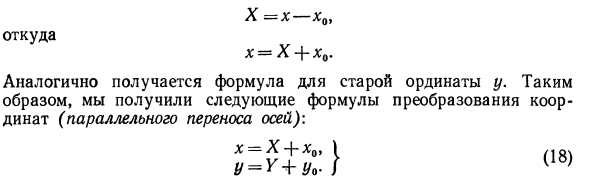

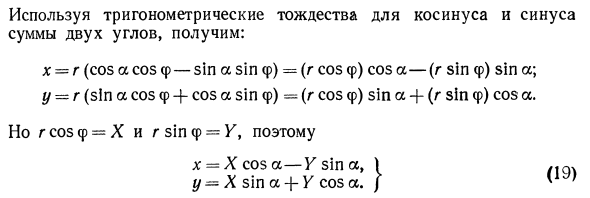

Преобразование координат
- Преобразование координат /. Перевод координатных осей Мы уже упоминали, что в некоторых случаях необходимо рассмотреть две системы координат на плоскости одновременно, чтобы решить следующую проблему: Выражение, которое выражает координаты точки в одной системе через координаты другой системы, называется выражением преобразования координат. В § 3 и 3 получена формула преобразования между декартовыми и полярными координатами. В этот момент предположим, что обе системы декартовы (прямоугольные), а оси одной и той же системы параллельны и обращены в одном направлении.
Я согласен называть координаты точки системы Ohu старыми, а координаты точки системы OtXY новыми. Пусть x0 и y0 — координаты нового старта 01 старой системы. Предположим, что произвольно выбранная точка M на плоскости имеет старые координаты x и y и новые координаты X и Y. Выведите формулу, которая представляет старые координаты точки M с новыми координатами.
На рисунке 33 показаны две такие системы, Ohu и OtXY. Система OXCU может быть получена путем перевода осей OX и OY. Людмила Фирмаль
Проецируя новый начальный Oy, точка M на оси OX и точка M на оси OX дают точки A, P и N соответственно. Но OxN- | X |, AP = \ x-x0 \, поэтому Рисунок 33 О себе XI = \ x — x, То есть абсолютное значение новой абсциссы X и разность x — x0 равны. Легко видеть, что эти величины имеют одинаковый знак. На самом деле, если N справа от O, P справа от A, а величины X и x — x0 оба положительны. Если N находится слева от Olt, X и x — x0 отрицательны, потому что P находится слева от A.
Оба случая Х = х — х0, Откуда Аналогично получается старое выражение по ординате y. Поэтому была получена следующая формула преобразования координат (движение по параллельной оси). х = х + х0 Y = Y + Yo
| Функциональная зависимость | Элементы теории определителей |
| Уравнение линии | Системы уравнений первой степени |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Пример. Точки O (2; -1) для системы Ohu. Если есть координаты –1 и 3 в новой начальной точке старой системы, найдите новые координаты X и Y путем параллельной передачи по оси. Из уравнения (18) 2 = Х-1, \ -1 = Т + 3, / Х = 3, Y = —4. Рисунок 34 2. Координата оси вращения Дайте две системы координат на плоскости с общим началом O. Система Oxy (старая) и система OXU (новая) получают старую систему, поворачивая ее на угол a. Средства, Угол (Ox, OX) = a (рис. 34), поэтому угол (0y> Oy) = a.
Найдите выражение, представляющее старые координаты x и y любой точки M на плоскости через новые координаты X и Y. Представление полярных координат: полярная ось, которая соответствует старой оси -Ox, и полярная ось, которая соответствует новой оси -OX. Задайте точке M в новой полярной системе координат полярный угол cp и полярный радиус r. В старой полярной системе координат полярный угол точки M равен + cp, а полярный радиус такой же, как в новой системе. Следовательно, согласно уравнению (7): x = r cos (a — (- φ), t / −r sin (a + φ).
Найдите выражение, представляющее старые координаты x и y любой точки M на плоскости через новые координаты X и Y. Людмила Фирмаль
Используя тригонометрические тождества для косинуса и синуса суммы двух углов: x = g (потому что cos f-sin a sin f) = (g cos q>) cos a- (g sin f) sin a; y = r (sin a cos f -f потому что sin f) — (g cos f) sin a -} — (g sin f) cos a. Где r cos f = X и r sin f = yy x = X cos a — K sin a, X sin a + Y cos a. Уравнение (19) называется типом вращения вала. Пример. Представьте старые координаты точек x и y с новыми координатами X и Y, когда ось повернута на угол a — Решения. = = тогда тогда по формуле (19) Получите следующее. Или х ^ (X-Y),

