Оглавление:
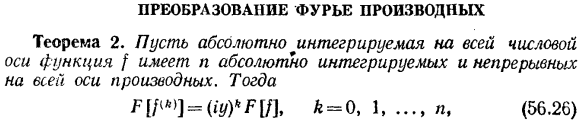



Преобразование Фурье производных
Преобразование Фурье производных. Теорема 2.Предположим, что функция /, которая может быть абсолютно интегрируемой по числовой оси, имеет непрерывную производную η, которая может быть абсолютно интегрируемой по оси. И затем… ^ [/1А)] =(* ’«)* ^ И. * = 0, 1П,(56.26) 56.8.Преобразование Фурье дифференцирования Четыреста пять И тогда есть постоянная M 0, которая равна: \ П [П ^ Т (56.27) Доказательство. Во-первых, возьмите только фактическое значение в функции/. Если /полностью интегрируема по оси со своей производной/и эта производная непрерывна、 /(*)= /(0)+ $Γ Да. 4-00 Потому что это интеграл§ / / ’(g) / по гипотезе теоремы、 +° Интеграл, Интеграл$ / ’ (), а также сходятся При делении интеграционной сходимости существует предел Пη (/’({)) (11 х +±ОО Отсюда и ограничения Pm /(x).
Выражение (56.26) доказывается, если n = 1. Для любого n он берется отсюда индуктивным методом. Людмила Фирмаль
- Кроме того, из конвергенции Х + + КО 4-00 § Интеграла заключается в том, что указанный предел равен нулю. −00 Пт /(х)=0.Применение интеграла по частям к формулам g * 4 03 Преобразование Фурье, мы получаем 4-00 КОМПАНИЯ. ^ НХ)е〜 ’ ху топор = 1yP [/]. 4-х Таким образом, когда вы дифференцируете функцию, ее преобразование Фурье умножается на коэффициент 1y. Где/ = «(to, если u и b-вещественные функции и снова их производные/ ’ = » + » / ’полностью интегрируемы и эта производная непрерывна、 Р [/ ’] = п [у’ + ВВ] = п [у ’] + 1П [в’] = 1yP [у] гг [о] = = 1мком [уа-Си \ = 1yP [/].
- Функция E [/’1)] ограничена(см. лемму 4). Таким образом, верхняя поверхность М является ЗІР / ’ [/(«] имеет конечное значение, поэтому оценка-Оо я / 4°°. (56.27) получается из Формулы k-Item$ 56 (56.26).Интегралы Фурье и преобразования Фурье 406. Заметим, что теорема 2, наряду с ее доказательствами, справедлива даже тогда, когда производная I-го порядка рассматриваемой функции не является непрерывной и имеет конечное число разрывов типа 1, сохраняя при этом остальные допущения (см.§ 5.1).
Таким образом, чем полнее интегрируемая производная функции, тем быстрее ее преобразование Фурье стремится к бесконечности и нулю. Людмила Фирмаль
- Фактически, в этом случае производная, обозначаемая любым конечным интервалом, является кусочно-непрерывной функцией (см. 28.3), и поэтому интегрирование части оправдано в доказательстве(см. 30.2 и 33.2). Упражнение 2.Докажите, что преобразование Фурье P (y) функции равно= = paBo o {-> as/ -°.
Смотрите также:
Решение задач по математическому анализу
| Интегралы Лапласа. | Свертка и преобразование Фурье. |
| Свойства преобразования Фурье абсолютно интегрируемых функций. | Производная преобразования Фурье функции. |

