Оглавление:










Преобразование Фурье интегрируемых в квадрате функций. Теорема Планшереля
Преобразование Фурье интегрируемых в квадрате функций. Теорема Планшереля. Если квадрат функции / интегрируется на всей действительной оси, то, как вы можете видеть из примера функции, сама функция/, в общем случае, не полностью интегрируется на всей оси /(*) Один ЕДИНОЕ ВРЕМЯ+ &Таким образом, нельзя утверждать о существовании преобразования Фурье функции пространства L ^(°°,°°°), на основе теории преобразований Фурье, которая описана в§ 56.In в этом случае мы указываем, что мы можем определить преобразование Фурье в некотором общем смысле. Сначала мы опишем определение пространства комплекснозначных функций (( ° , + ° C). Пусть / и§ 2 непрерывные функции, имеют квадратный модуль, который может быть интегрирован по оси и, вообще говоря, принимать сложные values. In в этом случае их скалярное произведение определяется по формуле +00 (/.?) = \ НХ) с (х) (1хКОМПАНИЯ.
В этом случае легко видеть, что все свойства, которые скалярное произведение должно иметь в сложном линейном пространстве, удовлетворены. Людмила Фирмаль
- 58.Регулярная основа и их развертывание 502. Пространство b2 (ω, ω), которое мы рассматриваем в этом разделе, определяется как завершение непрерывного предгильбертова пространства и имеет интегрируемый квадрат во всем модуле оси комплекснозначной функции c. скалярное произведение показано(§ 57. (См. теорему 6 III). Через| / ||в этом разделе показана норма элемента f€= 7-2 (oo, -} oo), то есть 1/1 = U1GZH Но… Также половина стандарта С приданными квадратную форму модулями которые можно интегрировать повсеместно в функция / ось. Для реальной функции без доказательства (см.§ 57.10) я отметил, что каждый элемент в пространстве b2 можно рассматривать как класс функции.
Пространство B2 комплекснозначной функции, а также семинорма| / / / функции/, совпадает с нормой элемента пространства b, к которому принадлежит функция/(в смысле, аналогичном показанному в§ 57.10).Мы не будем останавливаться на доказательствах этих фактов и не будем использовать их в будущем. Комплекснозначные функции f(x)=φ (x)+ *Φ ( * ), где φ(x) и φ (x) вещественные функции, -°°; x 4°°;функции конечного шага-это функции φ(x) и φ (x) (см. раздел 55.2, определение 7).в дальнейшем, чтобы быть кратким, функция конечного шага просто называется функцией шага. Любые 2-ступенчатые функции φ (x) и φ (x) могут быть представлены в виде конечной линейной комбинации тех же 1-ступенчатых функций, принимающих значения 1 и 0 (см.§ 55.2).
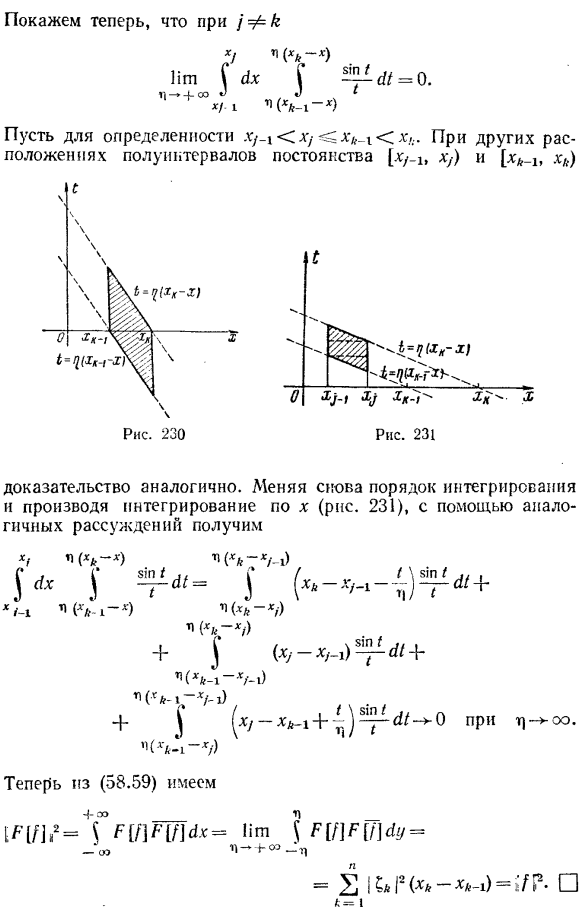
- Для этого используются интервалы постоянных функций φ (x) и φ (x). Эти пересечения делятся на полуинтервалы xk), k = 1, 2,…n. функции φ (x) и φ (x) являются постоянными одновременно. И так оно и есть. Н1. И*(Л) ХК-1-х, Если х с ХК. xk-r или x ^ xk, 1, 2,…если, н、 * Действительное%k, pA = 1, 2, если это соответствующая одношаговая функция… N присутствует. П П П Φ(*)= 1] КНО(х), Φ(х)= 2 р * ма(Т). / г = 1 к = 1 58,7*.Теорема плаш-Леле 503. Таким образом, шаговая функция f (x)=φ (χ)+ * Φ (χ) любого комплексного значения может быть выражена в следующем виде: П / ( * ) = 2 E и(). (58.56) 6 = 1 Где-K + qk, k = 1, 2,…, n-комплексное число. Лемма 6. / Как комплекснозначная шаговая функция и PS =ее преобразование Фурье、 ИИП[/] ВТОРОЙ = |! /!.
Доказательство. Если функция / задана в(58.56)、 + ОО Ш2= $Пх) пх) 0х= Да. П + ОЭ п = 2 $®/() У (Х) DX = 2 1 В2 (**(58.57) / , 6 = я-ОО 6 = 1 0 m] + oo; затем Д)С +00 +00 $ Е[/] [[/] ^ = ^ 5 ^ 5 [(х)е ^ ех $ с-Л-ОО-ое 4-ОО 4. ОЭ л = 2 ^ | Я НХ) Ж) А%§ * * & * Ый = * оо-оо-л 4-ОО + ое = 4 $ ($58.58) 00-00. Действительная и мнимая части функции f (x) удовлетворяют условиям теоремы о представлении функции с помощью интеграла Фурье (см. теорему 1 в§ 56.1), поэтому для всех x, кроме x-xk, k = 1, 2,… , n, мы имеем(см. доказательство этой теоремы)、 + 00 Золото 1 ^ +Утвердительный ответ Это говорит нам о том, что мы можем достичь предела под знаком интеграла как m]—+ oe в предположении при последнем интегрировании(58.58).
На самом деле, все интегралы происходят в конечных пределах, поэтому все преобразования здесь законны. Людмила Фирмаль
- Однако, поскольку соответствующая теорема не доказана в текущем курсе, необходимо сделать следующее: § 58.Регулярная основа и их развертывание 504. Дополнительный расчет. Если вы назначаете (58.56) на (58.58)、 П. ==! * ; _ 1х к! N х] Chhk по) = 1 2 S * I * * ^(58-59) 1.к = 1 х / 1■с(ХК.^икс) Подумайте о поведении каждой добавки в результирующей сумме как m] -|. / = & Если изменить порядок интегралов (рис. 230) и выполнить интегралы с переменной x, то получится: ХК ч(ХК-х) В результате функция φm= [[φ1] as—>равном сходится равномерно к преобразованию Фурье функции φ [[φ]. как видно, FA! Она сходится к функции φ в среднем в смысле / 12.By это, φ= .Вы можете легко увидеть, что это P [φ] (сравните аналогичные аргументы в доказательстве леммы 8). До сих пор преобразование Фурье(58.70) определялось только для этих электронов.
Смотрите также:
Решение задач по математическому анализу

