Оглавление:
Представление непериодической функции рядом Фурье
Пусть 
— непериодическая функция, заданная на всей числовой оси 
.
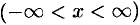Такая функция не может быть разложена в ряд Фурье, т. к. сумма ряда Фурье есть функция периодическая и, следовательно, не может
быть равна 
для всех 
.
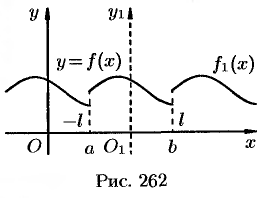
Однако непериодическая функция может быть представлена в виде ряда Фурье на любом конечном промежутке 
, на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка и построить функцию 
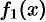периода 
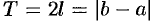такую, что 
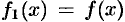при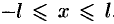 
. На рисунке 262 приведена иллюстрация построения функции .
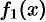Разлагаем функцию 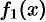в ряд Фурье. Сумма этого ряда во всех точках отрезка (кроме точек разрыва) совпадает с заданной функцией . Вне этого промежутка сумма ряда и являются совершенно различными функциями.
Пусть теперь непериодическую функцию требуется разложить в ряд Фурье на отрезке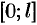 
. (Это частный случай: начало координат перенесено в точку 
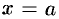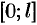отрезка ; область определения функции будет иметь вид , где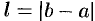 
.)
Такую функцию можно произвольным образом доопределить на отрезке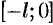 
, а затем осуществить ее периодическое продолжение периодом 
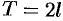. Разложив в ряд Фурье на отрезке 
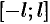полученную таким образом периодическую функцию 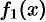, получим искомый ряд для функции при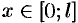 
.
В частности, функцию можно доопределить на отрезке 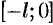четным образом (т. е. чтобы при 
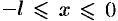было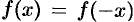 
) — см. рис. 263. В этом случае функция разлагается в ряд Фурье, который содержит только косинусы (см. формулы (67.8) и (67.9)).
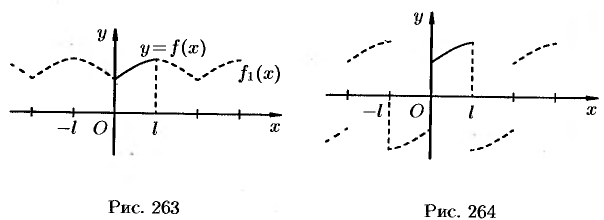
Если же функцию продолжить на отрезок 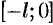нечетным образом (см. рис. 264), то она разлагается в ряд, состоящий только из синусов (см. формулы (67.10) и (67.11)).
Ряд косинусов и ряд синусов для функции , заданной на отрезке , имеют одну и ту же сумму. Если 
— точка разрыва функции , то сумма как одного, так и другого ряда равна одному и тому же числу: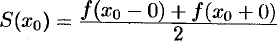 
.
Замечание. Все, что было сказано о разложении в ряд Фурье функции на отрезке 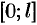, переносится практически без изменения на случай, когда функция задана на отрезке 
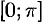; такую функцию можно разложить как в ряд косинусов, так и в ряд синусов (формулы (67.1) и (67.3)).
Пример №67.4.
Разложить в ряд косинусов функцию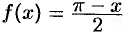 
, 
.
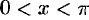Решение:
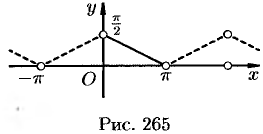
Продолжим функцию на отрезок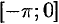 
четным образом (см. рис. 265). Разлагаем в ряд функцию
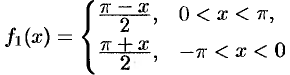
с периодом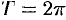 
. Условиям теоремы Дирихле функция 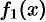удовлетворяет. Используя формулы (67.1) и (67.2), находим:
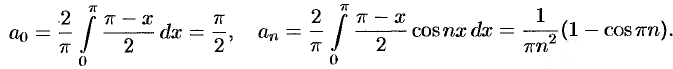
Таким образом,
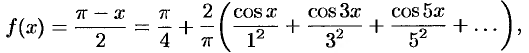
где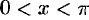 
при этом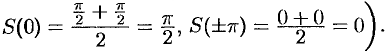 
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Разложение в ряд Фурье четных и нечетных функций |
| Разложение в ряд Фурье функций произвольного периода |
| Комплексная форма ряда Фурье |
| Интеграл Фурье |
