Оглавление:


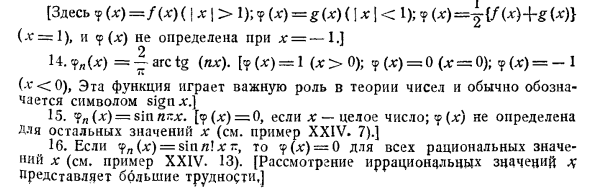
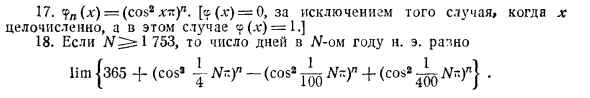
Представление функций непрерывного действительного переменного с помощью пределов
- Представление функции непрерывных вещественных переменных с использованием ограничений. В предыдущем абзаце мы часто рассматривали следующие ограничения: Нх <? «(*) н ~ * оо Линии как «1 () тиит = um K () + u2 (x) H —- + 11 n (*) b p- * s Где функция / z, которую мы ищем, содержит другую переменную x в дополнение к n. В таких случаях предел, конечно, является функцией от х. Так встретил функцию в пункте 75 f (x) = lim n x-1); «- ♦ и Сумма геометрических последовательностей 1 — \ — x -4 …
Глава Как считают многие читатели в приведенных ниже примерах, «очень« неестественная »» функция нерва имеет очень простое представление о типе проблемы. Пример XXXI. I. () = где n не вводит никакого выражения для yn (x), cp () = Km?
I (A-) = * для всех значений .v. х 2-? „(X) = -, где 0, (x) — + oo, если x <0, (x) -oo. Людмила Фирмаль
| Общие теоремы о бесконечных рядах | Грани ограниченной функции |
| Бесконечная геометрическая прогрессия | Верхний и нижний пределы ограниченной функции |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Только когда x = 0, yn (x) имеет конечный предел на η- оо, т. Е. 0. Таким образом, если x = 0, g (x) = 0 и не определено ни для какого другого значения x. л / х 1 ПХ 5. 1); v (x) не определено для q = -1,1 ° 0, докажите, что функция ^, ^ идет к пределу η- оо, и ограничение имеет три различных значения в следующих трех случаях: x <\, x- \ и x> 1. (Пример 1935 г.) Смотрите также особенности php-1 x «-I l> +1» * 11. 9 (*) =: 1 (| lg [> 1), -1 (| lg | <1) и? Создайте пример, где (Lg) = 0 (lr = 1 и ln = -1). _1 \ * л xTfl) ‘x ^ + x-n + n-
[Здесь 7 (x) = f <*) (| x |> 1); y (x) = g (x) (\ x \ <1); (X) ^ {f (x) + g {x)} (q = 1) и (x) не определены для q = -1. ] 1 ■ *. ? * () = ^ Arctg (yal :). [ 0); «P () = 0 (x = 0); 7 (x) = -I 4% (■ v «<0), эта функция играет важную роль в теории чисел и обычно обозначается символом .] 15. (дг) = ситипг.х. [) = sin / z! Для Arr y (x) = 0 для всех рациональных значений x (см. Пример XXIV, 13). [Очень трудно рассмотреть иррациональный смысл X. ]‘f „(x) — (cos2хт.у1. [В (л:) — 0. Однако, если х не является целым числом, <? (.Г) -1.] 18.
Для N ^ 1 753 целевое число дней для jV-om n. е. различный lim | zb5 + (cos ‘1 Nr.y- (cos2 u N ^ f + (cos2 ^ Wn) «}. Людмила Фирмаль

