Оглавление:


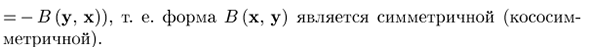

Представление билинейной формы в конечномерном линейном пространстве
- Представление конечномерной линейной билинейной формы Девять пространства. Давайте сделаем n-мерное линейное пространство L Билинейная форма B (x, y) задана. Уточнить проблемы с представлением Если L имеет четкий базис, e = форма B (x, y) = (E e2, …, en). Следующее предложение верно.
- Теорема 7.1. Билинейная форма B (x, y) указанной n меры Линейное линейное пространство L базиса e = (ei, B2, …, en) имеет вид Это четко выражено следующим образом: B (x, y) = где bij = B (ei ej), G.4) И & и r] j — это координаты, основанные на e векторов x и y соответственно. Доказательство. x = ^ Γ = 1 ^ e * и Y = ^ 7j = ir1jej ~
Поскольку разложение B (x, y) векторов x и y относительно базы e является линейным. Людмила Фирмаль
Для каждого из аргументов x и y (см. G.1)), тогда ( g, j = 1 Таким образом, для формы B (х, у) G.3) Для коэффициента bc в уравнении G.4). Чтобы доказать уникальность этого представления, Выражение G.3) для B (x, y) состоит из нескольких коэффициентов По фактору б ^. G.3) Как только x = e ^, y = e, Уравнение G.4) Для коэффициента bc. Теорема доказана.
Матрица определения Bb b12 … b1n \ B (e) = Bn1 b2 … bt G.5) Его элемент bj определяется с использованием соотношения G.4) Матрица билинейной формы B (x, y) этого базиса e. Замечания 1. Посмотрите на проблему построения всех линий покупок. Форма в данном конечномерном вещественном пространстве L Ответ на этот вопрос: Любая квадратная матрица (б) Исходя из этого, e = (ei, b2, …, en) является матрицей Билинейный формат.
Я проверю правильность этого утверждения. Определим в линейном пространстве L с заданным базисом e = = (Ei, b2, …, en) использовать матричную (bc) числовую функцию Два векторных аргумента x = EG = i ^ e * и Y = B (x, y) = Ej = Форма B i% ej (x, y) = E ™ j = i ^ j &% — Легко видеть, что эта функция отвечает всем условиям определения. Билинейное разбиение. Но тогда, согласно теореме 7.1, элемент Bij данной матрицы равен B (e ^, e ^)
- Существует выражение этого формата в формате G.3). Согласно замечаниям, естественно назвать Билинейная форма B (x, y) формулировка G.3 в общем виде билинейной формы) В n-мерном линейном пространстве. Замечание 2. Когда B (x, y) симметричен (кососимметричен) Билинейная форма, затем матрица G.5 этой формы с базисом е) Симметричный (косая симметрия).
Справедливый и обратный новый — когда билинейная форма B (x, y) матрица G.5) симметрична (Косая симметрия), билинейная форма симметрична (Косая симметрия). Я проверю правильность этого утверждения. Пусть B (x, y) — симметричная (кососимметричная) билинейная Форма.
Предполагая, что х = е ^ и у = е ^ в отношении G.2) Но г.4) bij = bji, (bj = -bji), G.6) Людмила Фирмаль
Другими словами, матрица G.5) является симметричной (кососимметричной). Здесь мы делаем матрицу G.5) в билинейной форме B (x, y) симметричной. Симметричный (косая симметрия), то есть элемент соответствует G.6). Тогда отношение G.3) и отношение B (x, y) = = Yllj = ibij ^ iVj, поэтому B (x, y) = H (y, x), (B (x, y) = = -B (y, x)), то есть форма B (x, y) симметрична (наклонена) Метрика).
Смотрите также:
| Решение полной проблемы собственных значений методом вращений | Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы |
| Понятие билинейной формы | Квадратичные формы |

