Предмет, задачи и основные понятия кинематики
Кинематикой называется раздел теоретической механики, изучающий механическое движение материальных тел лишь с геометрической стороны, вне зависимости от действующих на них сил.
Рассматривая движение тел как процесс непрерывного во времени изменения их положения в пространстве, кинематика оставляет в стороне вопрос о связи этого движения с материальной структурой тел и действующими на них силами. Подобно этому поступают в геометрии, в которой, изучая пространственные свойства тел, оставляют в стороне все остальные материальные признаки (вес, твердость и т.д.). Движущееся тело, следовательно, рассматривается в кинематике как некоторый геометрический образ.
Кинематика целиком основывается на аксиомах и положениях геометрии, но отличается от нее тем, что кроме пространства, проходимого движущимся телом, она рассматривает еще и время, за которое совершается это движение.
Кинематика имеет весьма важное значение не только для изучения последнего раздела теоретической механики — динамики, но и для исследования геометрических свойств движения частей различного рода механизмов.
Прогресс техники, задачи конструирования сложных механизмов и машин и привели в первой половине XIX века к выделению кинематики в самостоятельный раздел теоретической механики. Дальнейшее развитие кинематики в настоящее время также идет, главным образом, по пути ее приложения к конструированию и исследованию механизмов и машин.
Пространство и время, входящие в понятие движения, представляют собой формы существования материи, без которых не мыслимы ни сама материя, ни ее движение. «В мире нет ничего, кроме движущейся материи, и движущаяся материя не может двигаться иначе, как в пространстве и во времени» (В. И. Ленин. «Материализм и эмпириокритицизм», 1948, стр. 158).
Всякое механическое движение материального тела мы можем наблюдать и изучать лишь по отношению к каким-либо другим телам. Если бы в пространстве находилось только одно тело и не было бы других, то мы вообще были бы лишены возможности судить об изменении положения этого тела и, следовательно, об его движении.
Система координат, связанная с телом, относительно которого рассматривается изучаемое движение, называется системой отсчета.
Движение одного и того же тела относительно разных систем отсчета может быть совершенно различным. Так, например, камень, брошенный вертикально вверх на палубе равномерно движущегося парохода, падает на то же место и движется, следовательно, по отношению к палубе по прямой. Для наблюдателя же, стоящего на берегу, он движется по кривой (параболе). Любое тело, находящееся в покое по отношению к Земле, движется по отношению к Солнцу и т. д. Абсолютно неподвижных тел в природе не существует, и потому принципиально невозможно установить какую-либо абсолютно неподвижную систему отсчета.
Таким образом, понятия «движение» и «покой» являются относительными понятиями и имеют смысл только при указании системы отсчета, относительно которой они рассматриваются. Если тело изменяет свое положение относительно выбранной системы отсчета, то про такое тело говорят, что оно движется относительно этой системы отсчета. Если же его положение относительно системы отсчета не изменяется с течением времени, то про такое тело говорят, что оно находится в покое по отношению к данной системе отсчета.
В технической практике за основную или «неподвижную» систему отсчета обычно берется система отсчета, неподвижная относительно Земли, и движение тел по отношению к этой системе отсчета принимается (условно) за абсолютное. Нужно заметить, что для целей кинематики, рассматривающей движение тел вне зависимости от сил, на них действующих, по существу неважно, движется ли в действительности или нет система, принятая за «неподвижную».
Движение тела считается известным тогда, когда мы имеем возможность определить его положение относительно выбранной системы отсчета в любой момент времени.
Время является скалярной, непрерывно изменяющейся величиной и рассматривается в задачах кинематики как независимая переменная величина (аргумент). Все другие величины, изменяющиеся с течением времени, рассматриваются как функции времени.
Подобно тому как положение точки на прямой определяется расстоянием ее от некоторой другой точки, так и данный момент времени t определяется промежутком времени, протекающим от некоторого другого момента, условно принимаемого в данной задаче за начальный момент времени, т. е. за начало отсчета времени. Для начального момента времени можно принять, следовательно, значение переменной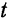 
равным нулю. Тогда моменты времени 
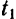и 
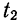будут определяться соответственно промежутками времен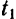и и 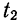, отделяющими их от начального момента времени, а промежуток времени 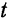между моментами времен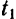и и 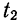— разностью 
.
Различные точки тела могут совершать, вообще говоря, различные движения. Поэтому изучение движения обычно начинается с так называемой кинематики точки, т. е. с установления геометрических характеристик движения отдельной материальной точки. Такой подход к изучению кинематики не является оторванной от практики абстракцией. Умея определять движение отдельных точек тела, мы сможем определить и движение тела в целом. Кроме того, как мы увидим в дальнейшем, для суждения о движении тела в целом иногда бывает достаточно знать движение только одной его точки.
В процессе своего движения точка последовательно занимает различные положения относительно принятой системы отсчета, причем эти положения непрерывно следуют одно за другим.
Геометрическое место всех последовательных положений движущейся точки называется траекторией этой точки.
Движение точки называется прямолинейным, если ее траектория — прямая линия, и криволинейным, если ее траектория — кривая линия.
Форма траектории зависит от выбора системы отсчета. Это ясно хотя бы из приведенного выше примера с камнем, брошенным на палубе движущегося парохода. Всякая классификация движений носит относительный характер и имеет смысл только тогда, когда эти движения рассматриваются относительно одной и той же системы отсчета.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
