Оглавление:

Термодина́мика (греч. θέρμη — «тепло», δύναμις — «сила»[K 1]) — раздел физики, изучающий наиболее общие свойства макроскопических систем и способы передачи и превращения энергии в таких системах. В термодинамике изучаются состояния и процессы, для описания которых можно ввести понятие температуры.
Термодинамика — это феноменологическая наука, опирающаяся на обобщения опытных фактов. Процессы, происходящие в термодинамических системах, описываются макроскопическими величинами (температура, давление, концентрации компонентов), которые вводятся для описания систем, состоящих из большого числа частиц, и не применимы к отдельным молекулам и атомам, в отличие, например, от величин, вводимых в механике или электродинамике. wikipedia.org/wiki/Термодинамика
Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «термодинамика».
Лекции подготовлены для студентов любых специальностей и охватывает полный курс предмета «термодинамика».
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Предмет термодинамики
Термодинамика — наука об энергии и ее свойствах — представляет собой важнейшую отрасль естествознания. Основой термодинамики служат два экспериментально установленных закона, называемых иначе первым и вторым началом термодинамики.
Термодинамика как самостоятельная наука получила развитие, когда были открыты эти два закона. Первый из них рассматривается как приложение к тепловым явлениям всеобщего закона сохранения и превращения энергии, а второй характеризует направление протекающих в окружающей нас природе процессов.
В зависимости от круга рассматриваемых вопросов и целей исследования термодинамику подразделяют на физическую, или общую, химическую и техническую.
В физической термодинамике даются представления об общих теоретических основах термодинамики и закономерностях превращения энергии в разнообразных физических явлениях (электрических, магнитных, поверхностных, капиллярных и др.). В химической термодинамике изучаются тепловой эффект различных химических реакций, расчет химического равновесия, исследуются свойства растворов и т. п.
Введение в термодинамику
Техническая термодинамика изучает применение законов термодинамики к процессам взаимного превращения теплоты и работы. Имея данные о действительном механизме процесса, всегда можно схематизировать каждый из реальных процессов так, чтобы можно было осуществить полный его термодинамический анализ.
Сущность этой схематизации состоит в том, что из совокупности всех участвующих в процессе тел выделяется рабочее тело, с помощью которого осуществляется данный процесс, а остальные тела рассматриваются как источники (и поглотители) теплоты. Такая совокупность тел, находящихся во взаимодействии, называется термодинамической системой.
Для определения полезной работы процесса и количества переданной теплоты, что составляет главное содержание прикладной части термодинамики, необязательно знать все особенности кинетики реального процесса. Вполне достаточно, чтобы наряду с внешними условиями, в которых протекает процесс, были известны лишь начальные и конечные состояния всех участвующих в процессе тел.
При этом для лучшего понимания физического смысла изучаемых процессов термодинамический метод анализа обычно сочетается с молекулярными и статическими исследованиями.
Основные параметры состояния газов
Процесс преобразования теплоты в работу осуществляется в тепловых двигателях с помощью рабочего тела. Обычно в качестве рабочего тела используются газы и пары, так как они обладают большим коэффициентом теплового расширения и могут при нагревании совершать гораздо большую работу, чем жидкости и твердые тела.
При теоретическом изучении газообразных тел (газов) обычно принято иметь дело с так называемым идеальным газом, между молекулами которого отсутствуют силы взаимодействия, а сами молекулы принимаются за материальные точки, не имеющие объема. В природе нет идеальных газов, но часто встречаются такие состояния реально существующих газов, у которых силы взаимодействия между молекулами и объемы самих молекул чрезвычайно малы. Поэтому под термином «идеальный газ» понимают газ, при изучении свойств которого можно пренебречь силами взаимодействия между молекулами и объемом самих молекул.
В теплотехнических расчетах вполне допустимо считать идеальными все газы, с какими приходится иметь дело (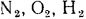 и т. д.).
и т. д.).
Исключение составляет водяной пар, который может встречаться в различных состояниях, а именно:
- водяной пар является частью газовых смесей, которые получаются в результате сгорания топлива в различных агрегатах. В этом случае парциальное давление пара мало, а температура пара высокая и он далек от состояния жидкости. Такой водяной пар можно считать идеальным газом. По этим же соображениям идеальным газом обычно считают и водяной пар, который входит как составная часть в атмосферный воздух;
- водяной пар является рабочим телом в паровых двигателях или теплоносителем в различных теплообменных аппаратах. В этом случае пренебрегать силами сцепления между молекулами и объемом самих молекул нельзя, так как его состояние близко к состоянию жидкости. В отличие от предыдущего водяной пар называется реальным газом, и он уже не подчиняется законам идеальных газов.
Состояние газа отражают средние величины, характеризующие результат действия молекул, образующих газ. Этим величинам присуще определенное значение для каждого отдельного состояния газа, и они носят название параметров состояния газа. В первую очередь рассмотрим основные параметры состояния газов: температуру, удельный объем и давление.
Под температурой газа понимают меру средней кинетической энергии движения молекул газа. В СССР применяют две температурные шкалы: термодинамическую и международную практическую. Температура по каждой из этих шкал может быть выражена двояким способом: в градусах абсолютной шкалы (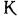 ) и в градусах Цельсия (
) и в градусах Цельсия (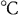 ) в зависимости от начала отсчета (положения нуля) по шкале.
) в зависимости от начала отсчета (положения нуля) по шкале.
Термодинамическая температурная шкала, принятая 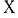 Генеральной конференцией по мерам и весам в 1954 г., имеет одну воспроизводимую опытным путем постоянную точку — тройную точку воды*, которая имеет значение 273,16
Генеральной конференцией по мерам и весам в 1954 г., имеет одну воспроизводимую опытным путем постоянную точку — тройную точку воды*, которая имеет значение 273,16 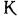 (точно), или 0,01
(точно), или 0,01 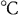 ; второй постоянной точкой служит абсолютный нуль температур.
; второй постоянной точкой служит абсолютный нуль температур.
Термодинамическая абсолютная температура обозначается 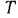 , а термодинамическая температура в градусах Цельсия —
, а термодинамическая температура в градусах Цельсия — 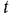 . Соотношение между
. Соотношение между 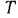 и
и 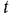 определяется по значениям температуры тройной точки воды:
определяется по значениям температуры тройной точки воды:
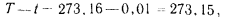
откуда
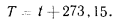
Международная практическая температурная шкала, принятая по решению 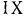 Генеральной конференции по мерам и весам в 1948 г., основана на шести постоянных и экспериментально воспроизводимых температурах фазового равновесия. Эта шкала является наиболее точным воспроизведением термодинамической шкалы температур, и разницу между ними практически можно не учитывать, поскольку она будет находиться заведомо за пределами точности экспериментальных данных. Вследствие близости обеих шкал обозначения температур по ним принимаем одинаковыми.
Генеральной конференции по мерам и весам в 1948 г., основана на шести постоянных и экспериментально воспроизводимых температурах фазового равновесия. Эта шкала является наиболее точным воспроизведением термодинамической шкалы температур, и разницу между ними практически можно не учитывать, поскольку она будет находиться заведомо за пределами точности экспериментальных данных. Вследствие близости обеих шкал обозначения температур по ним принимаем одинаковыми.
Второй параметр состояния газа — удельный объем 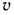 — представляет собой выраженный в кубических метрах объем 1 кг массы газа. Величина, обратная удельному объему, называется плотностью
— представляет собой выраженный в кубических метрах объем 1 кг массы газа. Величина, обратная удельному объему, называется плотностью 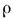 . Она представляет собой выраженную в килограммах массу 1
. Она представляет собой выраженную в килограммах массу 1 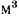 газа. Очевидно, что
газа. Очевидно, что  .
.
Третий параметр состояния газа — давление. Под давлением газа на стенки сосуда, в котором заключен газ, понимают средний результат ударов о стенки громадного числа молекул, из которых состоит газ. Давление Измеряют силой, действующей равномерно на единицу поверхности, и обозначают буквой 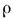 . В Международной системе единиц измерения
. В Международной системе единиц измерения 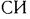 давление измеряется единицей
давление измеряется единицей 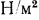 , которая называется «паскаль» (
, которая называется «паскаль» (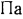 ). Поскольку в технике приходится встречаться с большими величинами давлений, то для их измерения пользуются единицами
). Поскольку в технике приходится встречаться с большими величинами давлений, то для их измерения пользуются единицами 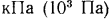 ,
, 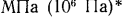 .
.
Давление газа можно измерить также высотой столба жидкости, соприкасающейся с этим газом. Действительно, если в каком-либо сосуде находится газ и этот сосуд с помощью 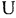 -образной трубки соединить с окружающей атмосферой, тогда жидкость, залитая в колено трубки, при абсолютном давлении газа, превышающем окружающее атмосферное (барометрическое) давление
-образной трубки соединить с окружающей атмосферой, тогда жидкость, залитая в колено трубки, при абсолютном давлении газа, превышающем окружающее атмосферное (барометрическое) давление 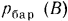 , займет такое положение, что уровень ее в правом колене трубки будет выше, чем в левом, на высоту
, займет такое положение, что уровень ее в правом колене трубки будет выше, чем в левом, на высоту 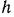 (рис. 1.1, а).
(рис. 1.1, а).
Разность 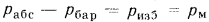 называется избыточным, или манометрическим давлением, так как оно измеряется с помощью манометров.
называется избыточным, или манометрическим давлением, так как оно измеряется с помощью манометров.
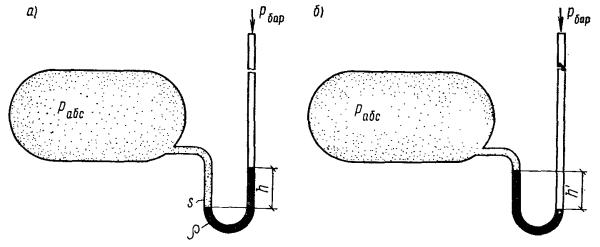
Рис. 1.1. Измерение давления газа в сосуде, когда оно выше атмосферного (а) и ниже атмосферного (б)
Если 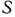 — площадь поперечного сечения трубки, а
— площадь поперечного сечения трубки, а 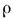 — плотность жидкости, находящейся в трубке, тогда сила
— плотность жидкости, находящейся в трубке, тогда сила 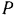 , с которой газ давит на жидкость, будет равна
, с которой газ давит на жидкость, будет равна 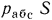 . С другой стороны, эта сила уравновешивается силами от барометрического давления и веса столба жидкости высотой
. С другой стороны, эта сила уравновешивается силами от барометрического давления и веса столба жидкости высотой 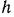 , т. е.
, т. е. 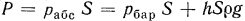 или
или

где 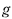 — ускорение свободного падения в месте измерения.
— ускорение свободного падения в месте измерения.
Пользуясь полученным равенством, можно легко установить соотношение, например, между 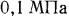 (давлением, близким к атмосферному) и высотой
(давлением, близким к атмосферному) и высотой 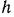 столба какой-либо жидкости.Так, для ртути при
столба какой-либо жидкости.Так, для ртути при 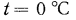 и нормальном ускорении свободного падения
и нормальном ускорении свободного падения 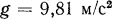 ,
, 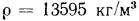 и
и 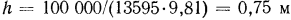 , т. е. для указанных условий
, т. е. для указанных условий  рт. ст.; для воды
рт. ст.; для воды 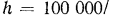
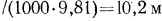 , откуда следует, что для тех же условий
, откуда следует, что для тех же условий 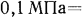
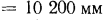 вод. ст. Давление, равное
вод. ст. Давление, равное 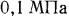 , или
, или 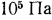 , называется бар.
, называется бар.
В связи с тем, что жидкость при повышении температуры расширяется, высота столба жидкости, соответствующая определенному давлению, также несколько увеличивается. Это положение следует иметь в виду, например, при переводе в 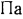 показаний ртутных барометров. Обычно показания барометров приводят к 0
показаний ртутных барометров. Обычно показания барометров приводят к 0 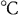 по формуле
по формуле

где 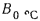 — высота ртутного столба при 0
— высота ртутного столба при 0 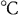 ;
; 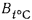 — высота ртутного столба при
— высота ртутного столба при 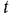
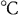 ;
; 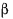 — температурный коэффициент объемного расширения жидкости (для ртути
— температурный коэффициент объемного расширения жидкости (для ртути 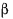 = 0,000172).
= 0,000172).
Если давление газа в сосуде меньше барометрического, уровень в левом колене будет выше, чем в правом, на величину 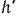 (рис. 1.1,б), которая показывает, насколько давление газа в сосуде ниже атмосферного, и называется разрежением (или вакуумом).
(рис. 1.1,б), которая показывает, насколько давление газа в сосуде ниже атмосферного, и называется разрежением (или вакуумом).
В физике за единицу измерения давления иногда принимают так называемую физическую атмосферу. Его давление, которое оказывает на основание ртутный столб высотой 760 мм при 0 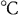 и нормальном ускорении свободного падения
и нормальном ускорении свободного падения 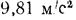 (точнее
(точнее 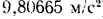 ). В технике эту единицу измерения давления не применяют, но она входит в определение так называемых нормальных физических условий (
). В технике эту единицу измерения давления не применяют, но она входит в определение так называемых нормальных физических условий (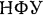 ), к которым приводят состояния различных газов при необходимости сравнения их между собой по объему. Нормальными физическими или просто нормальными условиями называются такие, при которых
), к которым приводят состояния различных газов при необходимости сравнения их между собой по объему. Нормальными физическими или просто нормальными условиями называются такие, при которых 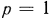 физ. ат. и
физ. ат. и 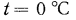 . Очевидно, 1 физ. ат.
. Очевидно, 1 физ. ат. 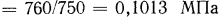 .
.
В молекулярно-кинетической теории газов доказывается, что давление газа численно равно 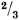 средней кинетической энергии поступательного движения молекул газа, заключенных в единице объема, т. е.
средней кинетической энергии поступательного движения молекул газа, заключенных в единице объема, т. е.

где 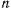 — число молекул, заключенных в единице объема;
— число молекул, заключенных в единице объема; 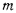 — масса молекулы;
— масса молекулы; 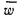 — средняя квадратичная скорость молекул.
— средняя квадратичная скорость молекул.
Умножая обе части уравнения (1.2) на заданный объем газа 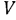 ,
, 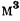 , получим
, получим 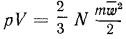 (где
(где 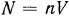 — число молекул в заданном объеме газа
— число молекул в заданном объеме газа 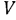 ).
).
Поскольку температура газа 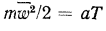 (где
(где 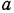 — коэффициент пропорциональности), тогда
— коэффициент пропорциональности), тогда

Полученное уравнение дает возможность легко установить ряд основных законов для идеальных газов. Если газ имеет постоянную температуру 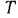 , то, поскольку
, то, поскольку 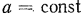 и
и 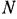 — число молекул в рассматриваемом объеме газа,
— число молекул в рассматриваемом объеме газа, 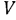 также постоянно:
также постоянно:

Если газ находится при постоянном давлении, то
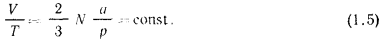
или для 1 кг газа
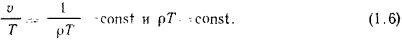
Произведение 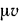 есть объем 1 моля газа*. Поэтому закон Авогадро можно сформулировать и таким образом: объем 1 моля различных газов при одинаковых физических условиях одинаков. Например, при
есть объем 1 моля газа*. Поэтому закон Авогадро можно сформулировать и таким образом: объем 1 моля различных газов при одинаковых физических условиях одинаков. Например, при 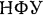 для кислорода
для кислорода 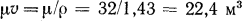 . Тогда при
. Тогда при 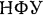 объем 1 кмоля всех газов будет равен 22,4
объем 1 кмоля всех газов будет равен 22,4 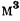 . Отсюда следует, что
. Отсюда следует, что

По равенству (1.8) определяют плотности различных газов при 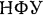 .
.
Уравнения состояния газов. Уравнение (1.3) для 1 кг газа имеет вид 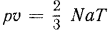 . Умножая левую и правую части этого равенства на молекулярную массу газа
. Умножая левую и правую части этого равенства на молекулярную массу газа 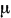 , получим
, получим

Так как 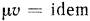 , то при одинаковых физических условиях в объеме 1 моля различных газов содержится одинаковое число молекул
, то при одинаковых физических условиях в объеме 1 моля различных газов содержится одинаковое число молекул 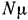 , которое носит название числа Авогадро.
, которое носит название числа Авогадро.
Обозначим 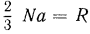 . Как видим,
. Как видим, 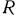 от состояния газа не зависит и поэтому называется газовой постоянной. Поскольку
от состояния газа не зависит и поэтому называется газовой постоянной. Поскольку 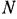 — число молекул в 1 кг, то
— число молекул в 1 кг, то 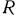 относится именно к этому количеству газа. Подставляя
относится именно к этому количеству газа. Подставляя 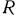 в уравнение (1.9), получим
в уравнение (1.9), получим 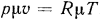 , откуда
, откуда 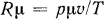 . Здесь
. Здесь 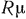 относится к 1 кмолю газа и называется киломольной газовой постоянной. Поскольку
относится к 1 кмолю газа и называется киломольной газовой постоянной. Поскольку 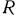 не зависит от состояния газа, вычислим
не зависит от состояния газа, вычислим 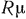 по известным параметрам
по известным параметрам 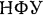 :
:
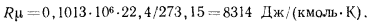
Как видим, киломольная газовая постоянная имеет одно и то же значение для всех газов, равное 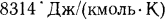 , поэтому она носит название универсальной газовой постоянной. Подставляя значение
, поэтому она носит название универсальной газовой постоянной. Подставляя значение 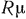 в равенство, из которого оно было определено, получим
в равенство, из которого оно было определено, получим

Это уравнение было получено в 1874 г. Д. И. Менделеевым и носит название уравнения состояния для 1 кмоля газа, или уравнения Менделеева—Клапейрона. Если уравнение (1.10) разделить на 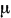 газа, получим
газа, получим
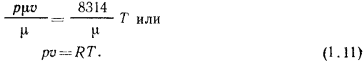
В уравнении (1-11) величина 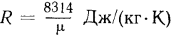 , как было указано, газовая постоянная; очевидно,
, как было указано, газовая постоянная; очевидно, 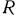 для каждого газа будет иметь свое вполне определенное значение.
для каждого газа будет иметь свое вполне определенное значение.
Уравнение (1.11) носит название уравнения состояния для 1 кг газа, или иначе оно называется также уравнением Клапейрона, который в 1834 г. вывел это уравнение как следствие из законов Бойля—Мариотта и Гей-Люссака. Если рассматривается процесс изменения состояния не 1 кг газа, а заданной массы 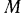 , кг, газа, то, умножая обе части уравнения (1.11) на
, кг, газа, то, умножая обе части уравнения (1.11) на 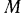 , получим
, получим
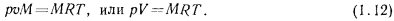
Это уравнение носит название уравнения состояния для 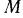 , кг, газа.
, кг, газа.
Уравнения (1.10)—(1.12) иначе называются также характеристическими (термическими) уравнениями состояния газа. Наиболее общим из этих трех уравнений является уравнение (1.10), так как оно содержит универсальную газовую постоянную 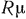 , одинаковую для всех газов.
, одинаковую для всех газов.
С помощью характеристических уравнений для любого состояния газа по двум известным его параметрам можно найти третий. Это доказывает, что у идеального газа произвольно можно изменять только два параметра его состояния, а третий параметр получится из уравнений состояния в соответствии с заданными двумя основными параметрами. Поэтому принято считать, что идеальный газ обладает двумя степенями свободы изменения параметров своего состояния.
Характеристические уравнения являются уравнениями равновесного состояния газа, т. е. такого, при котором давление, температура и плотность в каждый момент времени будут одинаковы во всей массе рассматриваемого газа. Если газ переходит из состояния, характеризуемого параметрами 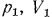 и
и 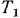 , в другое с параметрами
, в другое с параметрами 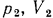 и
и 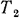 и это происходит таким образом, что в каждый отдельный момент газ находится в равновесном состоянии, то такой процесс называется равновесным.
и это происходит таким образом, что в каждый отдельный момент газ находится в равновесном состоянии, то такой процесс называется равновесным.
Возможно вам будет полезна эта страница:
| Задачи по термодинамике |
Смеси идеальных газов
Рассмотрены случаи, когда приходится иметь дело с каким-то вполне определенным газом, который по своим свойствам соответствует идеальному газу.
В теплотехнике обычно приходится встречаться не с отдельными газами, а с их смесями. Такие смеси часто образуются при горении топлива.
При рассмотрении смесей газов исходят из того, что смесь идеальных газов, не вступающих в химическое взаимодействие друг с другом, также является идеальным газом и подчиняется таким же законам. При этом каждый газ, входящий в состав газовой смеси, ведет себя так, как будто он один при данной температуре занимает весь объем смеси.
Давление, которое при этом оказывает каждый компонент смеси на стенки сосуда, называется парциальным, а давление газовой смеси складывается из парциальных давлений газов, образующих газовую смесь. Это положение составляет содержание закона Дальтона, установленного им для смесей газов опытным путем в 1807 г.
Математически этот закон записывается следующим образом:

где 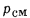 — давление смеси газов;
— давление смеси газов; 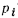 — парциальное давление
— парциальное давление 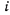 -го компонента, входящего в состав смеси;
-го компонента, входящего в состав смеси; 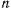 — число компонентов, образующих смесь.
— число компонентов, образующих смесь.
При расчете газовой смеси обычно определяют относительную молекулярную массу, газовую постоянную, плотность и парциальные давления компонентов, образующих смесь.
Состав газовой смеси может быть задан в массовых, объемных или мольных долях.
В первом случае, если обозначить массу смеси 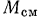 , а массу какого-то
, а массу какого-то 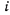 -го компонента —
-го компонента — 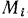 , то отношение
, то отношение 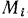 к
к 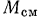 и определит массовую долю этого
и определит массовую долю этого 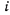 -го компонента, обозначаемую через
-го компонента, обозначаемую через 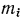 , т. е.
, т. е. 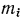
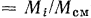 ; очевидно, что
; очевидно, что
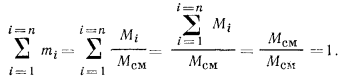
Во втором случае объем смеси и объем каждого компонента, входящего в смесь, одинаковы и по отдельности равны объему того сосуда, в котором находится смесь газов. При этом температура смеси и температура каждого компонента также одинаковы, а давления разные, ибо каждый из компонентов находится под своим парциальным давлением, а вся смесь под давлением, равным сумме этих парциальных давлений.
Чтобы сравнить количество газов, входящих в смесь, по объему, нужно объемы компонентов привести к одинаковому давлению, в качестве которого выбирают обычно давление смеси. Объемы компонентов, приведенные к давлению смеси, называются парциальными. Если объем смеси обозначить 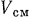 , а парциальный объем
, а парциальный объем 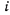 -го компонента —
-го компонента — 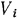 , то объемную долю
, то объемную долю 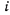 -го компонента
-го компонента 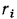 можно найти как отношение его парциального объема к объему смеси, т. е.
можно найти как отношение его парциального объема к объему смеси, т. е. 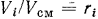 .
.
Чтобы найти
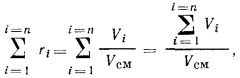
нужно определить, чему равна сумма парциальных объемов 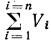 . Поскольку температура смеси и всех компонентов одинакова, напишем уравнение закона Бойля— Мариотта для
. Поскольку температура смеси и всех компонентов одинакова, напишем уравнение закона Бойля— Мариотта для 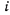 -го компонента при двух состояниях: когда он занимает объем смеси и находится под парциальным давлением и когда он занимает парциальный объем и находится под давлением смеси, т. е.
-го компонента при двух состояниях: когда он занимает объем смеси и находится под парциальным давлением и когда он занимает парциальный объем и находится под давлением смеси, т. е.

Если уравнение (1.14) написать для каждого компонента, входящего в состав газовой смеси, и просуммировать эти уравнения, будем иметь
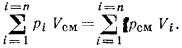
Но по уравнению (1.13) 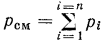 , тогда
, тогда
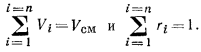
В третьем случае отношение числа молей 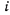 -го компонента
-го компонента 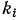 к числу молей смеси
к числу молей смеси 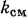 называется молярной долей
называется молярной долей 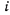 -го компонента, обозначаемой
-го компонента, обозначаемой 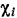 , т. е.
, т. е. 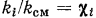 .
.
Следует иметь в виду, что молярные доли равны объемным долям, так как
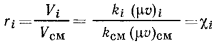
вследствие равенства объема молей по закону Авогадро.
Для упрощения расчетов газовую смесь условно заменяют смесью, состоящей из однородных средних молекул, которые по своему числу и суммарной массе могли бы заменить реальную смесь газов. Это упрощение дает возможность подойти к рассмотрению газовой смеси как к однородному газу.
Определим молекулярную массу смеси газов 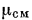 через массовые и объемные доли компонентов. Обозначим
через массовые и объемные доли компонентов. Обозначим 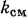 — число молей газовой смеси,
— число молей газовой смеси, 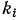 — число молей
— число молей 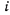 -го компонента, входящего в состав смеси. Число молей смеси
-го компонента, входящего в состав смеси. Число молей смеси 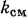 определим как сумму чисел молей компонентов смеси, т. е.
определим как сумму чисел молей компонентов смеси, т. е. 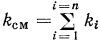 , тогда
, тогда
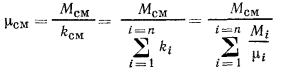
или

Для вычисления 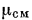 через объемные доли поступим так: пусть для упрощения
через объемные доли поступим так: пусть для упрощения  , тогда
, тогда
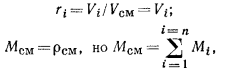
а 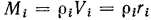 , следовательно,
, следовательно,

Эта формула, полученная как промежуточная в наших рассуждениях, может быть использована для определения плотности смеси через объемные доли компонентов. Так как 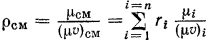 , а по закону Авогадро
, а по закону Авогадро 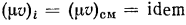 , то
, то
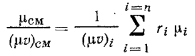
и окончательно

Газовая постоянная смеси газов 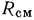 определяется из соотношения
определяется из соотношения

или
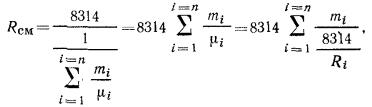
откуда

Плотность через массовые доли может быть определена по равенствам:
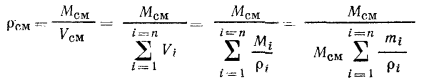
и

Удельный объем смеси 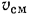 определяют как величину, обратную
определяют как величину, обратную 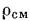 .
.
Парциальные давления компонентов 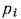 легко определить через объемные доли из уравнения (1.14):
легко определить через объемные доли из уравнения (1.14):
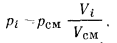
или

Через массовые доли 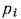 выражают следующим образом. Напишем уравнение состояния газа для смеси и для
выражают следующим образом. Напишем уравнение состояния газа для смеси и для 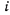 -ro компонента:
-ro компонента:
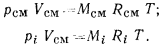
Разделив второе равенство на первое, получим:
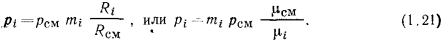
При расчете газовых смесей часто необходимо определять состав смеси по объемным долям, если известен массовый состав, и наоборот. Установим соответствующие формулы перехода
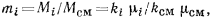
но
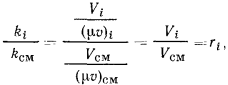
тогда:
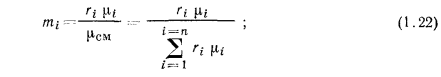
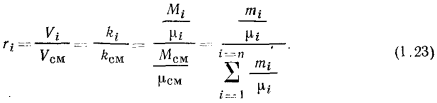
Теплоемкость идеальных газов
Под удельной теплоемкостью вещества понимают количество теплоты, которое нужно сообщить или отнять от единицы вещества (1 кг, 1 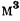 , 1 моль), чтобы изменить его температуру на 1 градус.
, 1 моль), чтобы изменить его температуру на 1 градус.
Теоретическими разработками и экспериментальными исследованиями установлено, что теплоемкость идеальных газов не зависит от их давления, а зависит лишь от его температуры.
Если теплоемкость относят к 1 кг газа, то ее принято называть массовой теплоемкостью и обозначать буквой 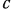 ,
, 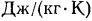 .
.
Если теплоемкость относят к 1 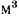 (взятому при нормальных условиях) или к 1 молю газа, то ее называют соответственно объемной или молярной и обозначают
(взятому при нормальных условиях) или к 1 молю газа, то ее называют соответственно объемной или молярной и обозначают 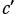 и
и 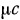 .
.
Соотношения между 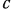 ,
, 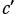 и
и 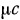 устанавливаются следующими равенствами:
устанавливаются следующими равенствами:

и

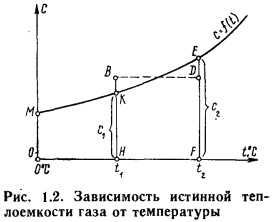
График зависимости теплоемкости от температуры показан на рис. 1.2. Как видим, с повышением температуры газа его теплоемкость растет и каждому значению температуры газа соответствует определенная теплоемкость, называемая истинной теплоемкостью газа, т. е. 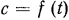 . Эту зависимость в явной форме принято выражать равенством
. Эту зависимость в явной форме принято выражать равенством
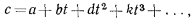
где 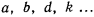 — постоянные для каждого газа величины, определяемые на основании экспериментальных или теоретических данных.
— постоянные для каждого газа величины, определяемые на основании экспериментальных или теоретических данных.
Если при температуре 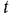 сообщить 1 кг газа бесконечно малое количество теплоты
сообщить 1 кг газа бесконечно малое количество теплоты 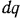 , температура газа изменяется также на бесконечно малую величину
, температура газа изменяется также на бесконечно малую величину 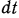 , тогда отношение
, тогда отношение 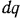 к
к 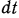 и будет являться истинной теплоемкостью газа при температуре
и будет являться истинной теплоемкостью газа при температуре 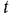 , т. е.
, т. е. 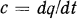 , откуда
, откуда

Очевидно, что количество теплоты 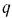 , которое сообщают 1 кг газа при нагревании его от начальной температуры
, которое сообщают 1 кг газа при нагревании его от начальной температуры 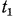 до конечной температуры
до конечной температуры 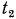 , определяют как
, определяют как 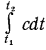 .
.
Для вычисления этого интеграла необходимо знать вид функции 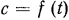 . Известно, что интеграл, выраженный уравнением (1.28), графически измеряется, площадью под кривой функции
. Известно, что интеграл, выраженный уравнением (1.28), графически измеряется, площадью под кривой функции 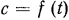 .
.
Тогда можно написать
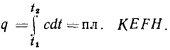
Если площадь фигуры 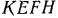 заменить площадью равновеликого ей прямоугольника
заменить площадью равновеликого ей прямоугольника 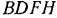 , построенного на том же основании
, построенного на том же основании 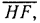 то высота этого равновеликого прямоугольника
то высота этого равновеликого прямоугольника 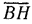 будет соответствовать средней теплоемкости в интервале температур от
будет соответствовать средней теплоемкости в интервале температур от 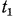 до
до 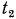 , т. е.
, т. е.
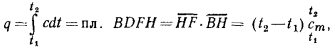
где 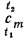 — средняя теплоемкость. В дальнейшем будем обозначать ее буквой
— средняя теплоемкость. В дальнейшем будем обозначать ее буквой 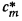 .
.
Таким образом,

Как следует из рис. 1.2, величина с зависит от крайних значений температур 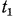 и
и 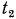 . Поэтому давать значения
. Поэтому давать значения 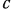 в виде таблиц для различных газов в любом произвольном интервале изменения их температур было бы слишком громоздко и неудобно. Во избежание этого поступают следующим образом.
в виде таблиц для различных газов в любом произвольном интервале изменения их температур было бы слишком громоздко и неудобно. Во избежание этого поступают следующим образом.
Площадь фигуры 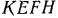 , которая графически соответствует количеству теплоты
, которая графически соответствует количеству теплоты 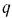 при нагревании газа от
при нагревании газа от 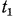 до
до 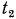 . представляют как разность площадей
. представляют как разность площадей 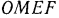 и
и 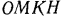 , т. е.
, т. е.
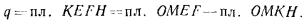
Площадь 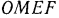 соответствует количеству теплоты, нужной для нагревания газа от температуры 0
соответствует количеству теплоты, нужной для нагревания газа от температуры 0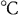 до температуры
до температуры 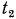 , а площадь
, а площадь 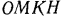 — количеству теплоты, требуемой для нагревания этого же количества газа от температуры 0
— количеству теплоты, требуемой для нагревания этого же количества газа от температуры 0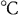 до температуры
до температуры 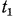 .
.
Каждая из этих площадей может быть в свою очередь представлена в виде равновеликих прямоугольников, высоты которых будут соответствовать средним значениям теплоемкостей в интервале изменения температур: для площадей 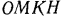 — от 0
— от 0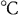 до
до 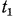 и для площадей
и для площадей 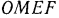 — от 0
— от 0 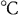 до
до 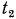 , т. е.
, т. е.

Последнее равенство дает возможность определить величину 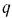 , если будут известны средние теплоемкости
, если будут известны средние теплоемкости 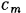 от 0
от 0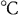 до любой заданной температуры
до любой заданной температуры 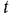 ,
, 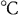 . Построенные по значениям средних теплоемкостей (см. прил. 1) кривые отражают нелинейный характер протекания функции
. Построенные по значениям средних теплоемкостей (см. прил. 1) кривые отражают нелинейный характер протекания функции 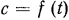 .
.
В некоторых случаях требуется, пользуясь таблицей теплоемкостей 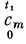 , найти значение теплоемкости
, найти значение теплоемкости 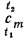 . Нетрудно видеть, что для этого можно использовать формулу
. Нетрудно видеть, что для этого можно использовать формулу

Необходимо отметить, что теплоемкость газов в большой степени зависит от тех условий, при которых происходят процессы их нагревания или охлаждения. В технике наиболее важное значение имеют процессы, протекающие при постоянном объеме газа (изохорный процесс) и при постоянном давлении газа (изобарный процесс).
Эти процессы подробно рассмотрены в гл. 3; здесь же нужно отметить, что в зависимости от этих процессов различают теплоемкость при постоянном объеме (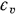 — массовая изохорная теплоемкость,
— массовая изохорная теплоемкость, 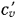 — объемная изохорная теплоемкость и
— объемная изохорная теплоемкость и 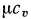 — молярная изохорная теплоемкость) и теплоемкость при постоянном давлении (
— молярная изохорная теплоемкость) и теплоемкость при постоянном давлении (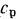 — массовая изобарная теплоемкость,
— массовая изобарная теплоемкость, 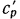 — объемная изобарная теплоемкость и
— объемная изобарная теплоемкость и 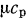 — молярная изобарная теплоемкость).
— молярная изобарная теплоемкость).
Для изменения температуры одного и того же количества газа на 1° требуется различное количество теплоты в зависимости от того, будет ли находиться газ при постоянном давлении или постоянном объеме.
Изобарная теплоемкость всегда больше изохорной, так как для нагрева 1 кг газа на 1° при 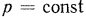 часть энергии расходуется на совершение работы, обусловленной расширением газа. Количественное соотношение между
часть энергии расходуется на совершение работы, обусловленной расширением газа. Количественное соотношение между 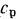 и
и 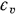 устанавливают с помощью уравнения Р. Майера, вывод которого дан в §3.1:
устанавливают с помощью уравнения Р. Майера, вывод которого дан в §3.1:

Если обе части уравнения (1.32) умножить на молекулярную массу газа 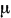 , получим
, получим
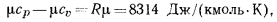
откуда
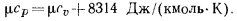
Таким образом, разность между молярными изобарной и изохорной теплоемкостями для всех газов — величина постоянная, равная 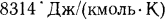 , или
, или 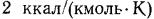 .
.
Молекулярно-кинетическая теория теплоемкостей, основанная на предположении о наличии жесткой связи между атомами в молекуле, доказывает, что для газов одинаковой атомности изохорные молярные теплоемкости сохраняют постоянное значение, равное числу степеней свободы перемещения молекул газа (если теплоемкость измеряется в ккал), т. е.:
для одноатомных газов:
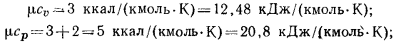
для двухатомных газов:
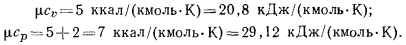
Эти значения достаточно хорошо совпадают с экспериментальными данными при температуре 15—20 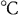 .
.
Для многоатомных газов такого соотношения не наблюдается, поскольку исходное положение указанной теории о наличии жесткой связи между атомами в молекуле современной наукой не подтверждается.
Молекулярно-кинетическая теория теплоемкостей не дает также ответа на вопрос, почему с увеличением температуры теплоемкость газа возрастает. Например, по опытным данным Всесоюзного теплотехнического института (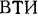 ), зависимость средней изобарной массовой теплоемкости для воздуха в пределах от 0 до 1500
), зависимость средней изобарной массовой теплоемкости для воздуха в пределах от 0 до 1500 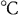 выражается равенством
выражается равенством
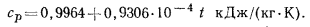
Правда, если изменения температуры газа невелики, допустимо теплоемкость в пределах процесса изменения состояния газа считать постоянной и принимать ее для одно- и двухатомных газов равной тем значениям, которые дает молекулярно-кинетическая теория газов. Это, естественно, упрощает выводы и расчеты. Так же поступают иногда и с трехатомными газами, принимая для них 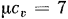 и
и 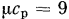
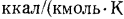 , что лучше согласуется с опытными данными, вместо
, что лучше согласуется с опытными данными, вместо 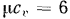 и
и 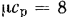
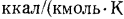 , которые дает молекулярно-кинетическая теория теплоемкостей.
, которые дает молекулярно-кинетическая теория теплоемкостей.
Молекулярная физика доказывает, что вследствие движения атомов внутри молекулы число степеней свободы перемещения молекулы увеличивается на число возможных связей между атомами в молекуле, т. е. трехатомный газ будет иметь число степеней свободы не 6, а 9, а четырехатомный — 12 и т. д.
Это положение учитывается в квантовой теории, согласно которой теплоемкость является функцией температуры, однако усиление колебательного движения атомов в молекуле оказывается непропорциональным повышению температуры. На основе выводов квантовой теории для определения мольной изохорной теплоемкости идеального газа применяют формулу Эйнштейна
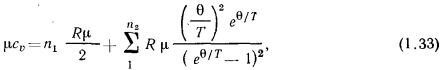
где 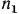 — число степеней свободы поступательного и вращательного движения молекулы;
— число степеней свободы поступательного и вращательного движения молекулы; 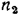 — число степеней свободы внутримолекулярных колебаний;
— число степеней свободы внутримолекулярных колебаний; 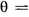
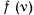 , здесь
, здесь 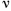 — число колебании в 1
— число колебании в 1 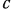 ;
; 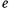 — основание натуральных логарифмов;
— основание натуральных логарифмов; 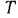 — температура газа.
— температура газа.
В этой формуле количество теплоты, расходуемой на увеличение поступательного и вращательного движения, учитывается первым членом и определяется числом степеней свободы 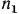 . Количество теплоты, расходуемой на увеличение внутримолекулярных колебаний, учитывается вторым слагаемым и определяется числом степеней свободы
. Количество теплоты, расходуемой на увеличение внутримолекулярных колебаний, учитывается вторым слагаемым и определяется числом степеней свободы 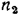 .
.
Для получения результатов на основе применения в расчетах молекулярно-кинетической теории теплоемкостей в формуле (1.33) надо отбросить второе слагаемое. Теплоемкость смесей газов будет, очевидно, определяться тем количеством теплоты, которое потребуется для того, чтобы нагреть 1 кг или 1 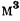 газовой смеси на 1°, а это в свою очередь будет определяться тем, что каждый компонент смеси во взятом количестве должен быть нагрет также на 1°, т. е. массовая теплоемкость смеси газов
газовой смеси на 1°, а это в свою очередь будет определяться тем, что каждый компонент смеси во взятом количестве должен быть нагрет также на 1°, т. е. массовая теплоемкость смеси газов 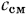 определится уравнением
определится уравнением

где 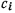 — массовая теплоемкость
— массовая теплоемкость 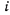 -го компонента.
-го компонента.
Объемная теплоемкость газовой смеси

где 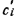 — объемная теплоемкость
— объемная теплоемкость 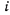 -го компонента.
-го компонента.
Первый закон термодинамики
Понятие о внутренней энергии газа
Внутренней энергией называется совокупность всех видов энергии, которыми обладает любое тело или система тел в данном состоянии, не связанных с движением системы как целого или с наличием внешнего силового поля (гравитационного, электрического, магнитного).
Поскольку в технической термодинамике изучаются лишь физические процессы, происходящие в тепловых и холодильных установках, будем рассматривать только те виды внутренней энергии, которые возникают при различных термодинамических процессах изменения состояния газов в зависимости от их основных параметров 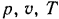 .
.
Внутренняя энергия обозначается буквой 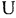 и является функцией этих параметров. Так как основные параметры состояния газа связаны между собой характеристическим уравнением, то внутреннюю энергию можно представить как функцию только двух основных параметров состояния газа, т. е.
и является функцией этих параметров. Так как основные параметры состояния газа связаны между собой характеристическим уравнением, то внутреннюю энергию можно представить как функцию только двух основных параметров состояния газа, т. е. 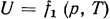 , или
, или 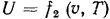 , или
, или 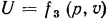 .
.
Вследствие того что температура газа определяет кинетическую энергию поступательного и вращательного движения молекул и энергию внутримолекулярных колебаний, а от давления или объема зависит потенциальная энергия, то внутренней энергией газа и называют сумму перечисленных четырех видов энергии молекул газа.
При этом под потенциальной энергией газа понимают энергию, обусловленную силами сцепления между его молекулами. Для данной температуры газа силы сцепления между молекулами зависят от расстояний между ними, определяемых давлением, под которым газ находится, или объемом, который он занимает.
Поскольку в общем случае внутренняя энергия газа является функцией двух основных параметров, а каждому состоянию соответствует вполне определенное их значение, то, следовательно, для каждого состояния газа будет характерна своя однозначная, вполне определенная величина внутренней энергии 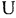 , т. е., иначе говоря,
, т. е., иначе говоря, 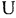 — это также функция состояния газа, и разность внутренних энергий для двух каких-либо состояний рабочего тела или системы тел не будет зависеть от того, каким путем это рабочее тело или система тел будет переходить из первого состояния во второе.
— это также функция состояния газа, и разность внутренних энергий для двух каких-либо состояний рабочего тела или системы тел не будет зависеть от того, каким путем это рабочее тело или система тел будет переходить из первого состояния во второе.
Математически разность внутренних энергий для двух состояний рабочего тела записывается так: 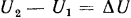 , где
, где 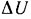 обычно называют изменением внутренней энергии, единица измерения которой, отнесенная к 1 кг газа, будет Дж/кг.
обычно называют изменением внутренней энергии, единица измерения которой, отнесенная к 1 кг газа, будет Дж/кг.
В идеальном газе силы сцепления между молекулами отсутствуют, следовательно, нет и потенциальной энергии, которая обусловлена наличием сил сцепления. Поэтому для идеального газа внутренняя энергия представляет собой функцию только температуры газа и только ею и определяется. Формулы для определения внутренней энергии.
Определение работы газа при его расширении
Рассмотрим процесс изменения состояния 1 кг газа в цилиндре с подвижным поршнем. Предполагается, что газ извне от какого-либо источника может получать теплоту. Если давление газа 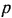 , а площадь поршня
, а площадь поршня 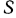 , то при действии на шток поршня внешнего усилия
, то при действии на шток поршня внешнего усилия 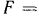
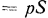 поршень, очевидно, будет находиться в неподвижном состоянии (рис. 2.1). При некотором уменьшении внешнего усилия
поршень, очевидно, будет находиться в неподвижном состоянии (рис. 2.1). При некотором уменьшении внешнего усилия 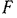 поршень за счет разности сил
поршень за счет разности сил  будет перемещаться вправо. Газ, находящийся под поршнем, начнет расширяться и совершать работу по преодолению внешних сил сопротивления. Задача состоит в том, чтобы дать аналитическое и графическое выражения работы газа при его расширении.
будет перемещаться вправо. Газ, находящийся под поршнем, начнет расширяться и совершать работу по преодолению внешних сил сопротивления. Задача состоит в том, чтобы дать аналитическое и графическое выражения работы газа при его расширении.
Чтобы иметь возможность при решении поставленной задачи пользоваться зависимостями между параметрами состояния газов и характеристическими уравнениями, справедливыми лишь для равновесных процессов, будем рассматривать такой процесс расширения газа, при котором:
- поршень перемещается в цилиндре с бесконечно малой скоростью. Это позволяет утверждать, что в каждый данный момент времени по всей массе газа давление будет одинаковым;
- разность температур между рабочим телом (газом) и источником, тепла бесконечно мала. Это позволяет утверждать, что в каждый данный момент времени по всей массе газа температура также будет одинаковой.
При таком процессе расширения газ в каждый рассматриваемый момент времени будет находиться в равновесном состоянии, т. е. давление, плотность и температура газа будут одинаковыми по всей его массе.
Подобные равновесные процессы изменения состояния газа, изучаемые в термодинамике, являются также обратимыми, т. е. такими, при которых рабочее тело проходит через одни и те же промежуточные равновесные состояния как в прямом, так и в обратном направлении, и никаких изменений в рассматриваемой изолированной системе, состоящей из источника теплоты, рабочего тела и приемника механической энергии, после окончания процесса не происходит.
Следовательно, в процессе сжатия газа затрачивается столько же работы, сколько ее получается при расширении, и от газа отводится столько же теплоты, сколько было ему сообщено. «Изолированной системы», так же как и «идеального газа», не существует, и это понятие вводят лишь для упрощения изучения ряда процессов изменения состояния газов.
Итак, для обратимых процессов необходимы следующие условия:
- бесконечно медленное изменение состояния рабочего тела;
- наличие бесконечно большого числа равновесных состояний рабочего тела;
- отсутствие внешнего и внутреннего трения между частицами рабочего тела и необратимого теплообмена с окружающей средой;
- отсутствие химических изменений в рабочем теле.
Все действительные процессы изменения состояния газов являются необратимыми, так как все процессы в тепловых установках протекают с конечными скоростями, и поэтому параметры состояния газа не могут быть в каждый момент времени одинаковыми по всей его массе.
Например, в процессе сжатия газа в цилиндре наибольшее давление будет в слоях газа, расположенных ближе к днищу поршня, а наименьшее давление — в слоях газа, наиболее удаленных от поршня.
Кроме того, при изменении состояния газов, например, в цилиндрах поршневых двигателей внутреннего сгорания изменяется химический состав рабочего тела и, следовательно, газовая постоянная 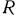 ; происходят потери теплоты с лучеиспусканием и при трении. Типичным примером необратимого процесса является трение. Работа, затрачиваемая на преодоление трения, необратимо превращается в теплоту, выделяющуюся при трении.
; происходят потери теплоты с лучеиспусканием и при трении. Типичным примером необратимого процесса является трение. Работа, затрачиваемая на преодоление трения, необратимо превращается в теплоту, выделяющуюся при трении.
Таким образом, необратимые процессы могут протекать только в одном направлении: в этом случае возвращение системы в исходное состояние невозможно.
После совершения необратимого процесса рассматриваемая система может быть возвращена в первоначальное положение только при затрате энергии извне. Чем больше отклоняется необратимый процесс от обратимого, тем меньшая часть работы газа передается к приемнику механической энергии и больше тратится на необратимые потери (трение, теплообмен и т. п.).
Строго говоря, необратимые процессы нельзя изобразить графически, так как уравнение состояния  нельзя применять для неравновесных состояний. Однако опыт показывает, что при расчетах тепловых установок можно пренебречь неравновесностью состояний без грубых погрешностей и, принимая в качестве давления и температуры газа некоторые средние величины по объему, рассчитывать по ним термодинамические процессы.
нельзя применять для неравновесных состояний. Однако опыт показывает, что при расчетах тепловых установок можно пренебречь неравновесностью состояний без грубых погрешностей и, принимая в качестве давления и температуры газа некоторые средние величины по объему, рассчитывать по ним термодинамические процессы.
Результаты исследований обратимых процессов дают возможность выявить условия наивыгоднейшего проведения реальных процессов. Поэтому действительные необратимые процессы изучают, заменяя их такими обратимыми процессами, которые приводят к одинаковым с необратимыми конечным состояниям рабочего тела.
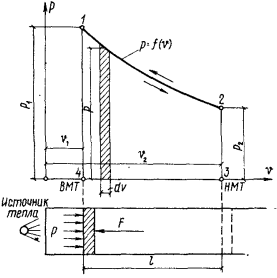
Вернемся теперь к решению поставленной выше задачи по определению работы газа при его расширении. В соответствии с предположением о бесконечно малой скорости перемещения поршня в цилиндре разобьем весь процесс расширения на бесконечно малые элементы с отрезком пути 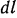 поршня в каждом (см. рис. 2.1). Тогда для каждого элементарного отрезка пути перемещения поршня
поршня в каждом (см. рис. 2.1). Тогда для каждого элементарного отрезка пути перемещения поршня 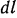 элементарная работа
элементарная работа 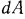 может быть определена как произведение силы на путь, т. е.
может быть определена как произведение силы на путь, т. е. 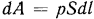 , но так как
, но так как 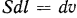 , то
, то

Работа, совершаемая 1 кг газа при его расширении, может быть найдена как сумма элементарных работ 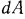 при перемещении поршня на всем пути
при перемещении поршня на всем пути 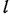 , т. е.
, т. е.

Работу, совершаемую при расширении газа, называют также технической.
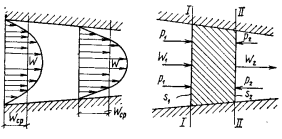
Для графического определения работы удобно пользоваться диаграммой, на которой по оси абсцисс откладывают значения удельного объема газа 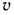 , соответствующие отдельным положениям поршня в цилиндре, а по оси ординат — устанавливающееся при этом давление
, соответствующие отдельным положениям поршня в цилиндре, а по оси ординат — устанавливающееся при этом давление 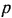 (см. рис. 2.1).
(см. рис. 2.1).
Если получившиеся на этой диаграмме отдельные точки, каждая из которых характеризует состояние газа в цилиндре при определенном положении поршня, соединить между собой плавной кривой то получится линия 1—2, характеризующая направление процесса изменения состояния газа в цилиндре при перемещении поршня.
Тогда элементарная работа 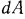 графически будет выражена заштрихованной площадкой элементарного прямоугольника с основанием
графически будет выражена заштрихованной площадкой элементарного прямоугольника с основанием 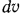 и высотой
и высотой 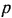 , а полная работа расширения газа
, а полная работа расширения газа 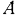 — площадью под кривой 1—2, равной сумме элементарных площадок, каждая из которых соответствует
— площадью под кривой 1—2, равной сумме элементарных площадок, каждая из которых соответствует 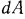 . Указанное положение непосредственно следует также из уравнения (2.2), в котором подынтегральное выражение представляет собой функцию
. Указанное положение непосредственно следует также из уравнения (2.2), в котором подынтегральное выражение представляет собой функцию 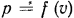 , графически изображаемую кривой 1—2. Следовательно, площадь под этой кривой является графическим выражением интеграла
, графически изображаемую кривой 1—2. Следовательно, площадь под этой кривой является графическим выражением интеграла 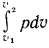 , т. е. работы
, т. е. работы 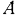 .
.
Система осей координат, представленная на рис. 2.1, называется 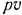 -диаграммой, широко используемой в термодинамике для анализа различных процессов изменения состояния газов. Поэтому работу расширения газа графически изображают в
-диаграммой, широко используемой в термодинамике для анализа различных процессов изменения состояния газов. Поэтому работу расширения газа графически изображают в 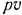 -диаграмме площадью, ограниченной кривой процесса 1—2, отрезком оси абсцисс 3—4 и двумя крайними ординатами процесса 2—3 и 4—1.
-диаграмме площадью, ограниченной кривой процесса 1—2, отрезком оси абсцисс 3—4 и двумя крайними ординатами процесса 2—3 и 4—1.
Если при изменении состояния газа объем его уменьшается, т. е. совершается сжатие (процесс идет от точки 2 к точке 1, см. рис. 2.1), то работу 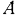 определяют по тому же уравнению (2.2), но при подсчете она получается отрицательной, так как начальный объем в этом случае
определяют по тому же уравнению (2.2), но при подсчете она получается отрицательной, так как начальный объем в этом случае 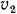 будет больше конечного
будет больше конечного 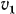 .
.
Физический смысл отрицательной работы состоит в том, что не газ совершает работу, а внешние силы, приложенные к газу, т. е. поршень в цилиндре будет перемещаться за счет внешнего усилия, которое на него действует. Естественно, что для аналитического вычисления работы газа по уравнению (2.2) нужно знать вид функции 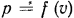 или, иначе говоря, путь процесса изменения состояния газа.
или, иначе говоря, путь процесса изменения состояния газа.
Возможно вам будет полезна эта страница:
| Методические указания по термодинамике |
Аналитическое выражение первого закона термодинамики
Первый закон термодинамики является основой термодинамической теории и имеет огромное прикладное значение при исследовании термодинамических процессов, так как позволяет установить их энергетические балансы.
Первый закон термодинамики фактически является законом сохранения и превращения энергии, отражающим особенности вечно движущейся и вечно изменяющейся материи. Впервые закон сохранения и превращения энергии в четкой форме был установлен М. В. Ломоносовым.
Сущность этого закона, как известно, состоит в том, что энергия не создается и не уничтожается, различные формы энергии могут превращаться одна в другую в строго эквивалентных соотношениях. Это позволило Ф. Энгельсу сформулировать закон сохранения и превращения энергии, а следовательно, и первый закон термодинамики, следующим образом: «… любая форма движения способна и вынуждена при определенных для каждого случая условиях превращаться прямо или косвенно в любую другую форму движения».
Это означает, что если 1 кг газа в рассматриваемой системе, которая находится в равновесии с окружающей, средой, сообщается 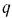 единиц теплоты и при этом изменение внутренней энергии 1 кг газа составляет
единиц теплоты и при этом изменение внутренней энергии 1 кг газа составляет 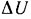 , то как бы «исчезнувшее» количество теплоты представится разностью
, то как бы «исчезнувшее» количество теплоты представится разностью 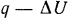 , и если этот килограмм газа совершает количество работы, равное
, и если этот килограмм газа совершает количество работы, равное 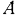 , то, согласно первому закону термодинамики, должно существовать равенство
, то, согласно первому закону термодинамики, должно существовать равенство
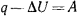 , или
, или 
Уравнение (2.3) является математической формулировкой первого закона термодинамики для любых процессов, по которому теплота, сообщаемая газу, расходуется на изменение внутренней энергии газа и на совершение газом работы расширения.
В дифференциальной форме, когда 1 кг газа сообщается бесконечно малое количество теплоты 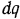 , уравнение первого закона термодинамики принимает вид
, уравнение первого закона термодинамики принимает вид

или

Каждый из трех членов написанных уравнений может быть положительной или отрицательной величиной, а в некоторых случаях равной нулю. Так, термодинамике принято, что если теплота сообщается рабочему телу, то 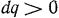 ; если же теплота отнимается от рабочего тела, то
; если же теплота отнимается от рабочего тела, то  .
.
При расширении газа, т. е. когда он совершает работу по преодолению сил внешнего сопротивления, 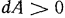 ; при сжатии газа конечный объем его меньше начального, а на это затрачивается работа извне и
; при сжатии газа конечный объем его меньше начального, а на это затрачивается работа извне и 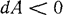 . Очевидно, при
. Очевидно, при 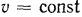
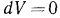 и
и 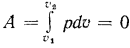 и вся теплота, сообщаемая газу, расходуется только на увеличение его внутренней энергии, а отвод теплоты возможен только вследствие уменьшения внутренней энергии, т. е.
и вся теплота, сообщаемая газу, расходуется только на увеличение его внутренней энергии, а отвод теплоты возможен только вследствие уменьшения внутренней энергии, т. е. 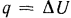 . Но по уравнению (1.29)
. Но по уравнению (1.29) 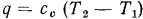 , тогда:
, тогда:

и

Поскольку изменение внутренней энергии не зависит от характера процесса и для идеального газа внутренняя энергия является функцией только температуры, то формула (2.5) будет общей для определения изменения внутренней энергии идеального газа во всех термодинамических процессах, в которых температура газа изменяется от 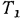 до
до 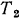 . Очевидно, что при
. Очевидно, что при 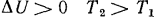 и при
и при 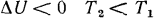 .
.
Интерес представляет изменение внутренней энергии, а не ее абсолютное значение. Поэтому начало отсчета внутренней энергии не имеет значения. Обычно его принимают или при 0 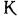 , или при 0
, или при 0 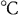 .
.
Изменение внутренней энергии реального газа при условии, когда нельзя пренебречь изменением потенциальной энергии молекул, можно определить по таблицам или специальным диаграммам, составленным для этой цели.
Величины 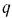 и
и 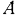 не являются параметрами состояния газа, как, например,
не являются параметрами состояния газа, как, например, 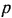 ,
, 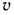 ,
, 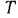 ,
, 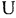 , так как характеризуют не состояние рабочего тела, а процесс его изменения и зависят от того, каким образом он совершается, т. е. от того, как газ переходит из начального состояния, характеризуемого точкой 1, в конечное состояние, характеризуемое точкой 2.
, так как характеризуют не состояние рабочего тела, а процесс его изменения и зависят от того, каким образом он совершается, т. е. от того, как газ переходит из начального состояния, характеризуемого точкой 1, в конечное состояние, характеризуемое точкой 2.
Действительно, 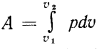 , т. е. работа определяется видом функции
, т. е. работа определяется видом функции 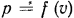 и, как указано в § 2.2, в
и, как указано в § 2.2, в 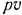 -диаграмме работа измеряется площадью, ограниченной сверху кривой этой функции. Таким образом, работа, совершаемая газом в любом процессе, будет определяться его направлением.
-диаграмме работа измеряется площадью, ограниченной сверху кривой этой функции. Таким образом, работа, совершаемая газом в любом процессе, будет определяться его направлением.
Что же касается количества теплоты 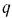 , подводимой к газу в процессе изменения его состояния, то из уравнения первого закона термодинамики
, подводимой к газу в процессе изменения его состояния, то из уравнения первого закона термодинамики 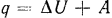 следует, что правая его часть, куда входит
следует, что правая его часть, куда входит 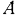 , зависит от направления процесса. Следовательно, и левая часть этого уравнения, т. е.
, зависит от направления процесса. Следовательно, и левая часть этого уравнения, т. е. 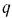 , также зависит от направления процесса изменения состояния рабочего тела. Следовательно, теплота
, также зависит от направления процесса изменения состояния рабочего тела. Следовательно, теплота 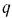 и работа
и работа 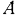 являются функциями процесса изменения состояния рабочего тела.
являются функциями процесса изменения состояния рабочего тела.
Уравнение первого закона термодинамики для газового потока и понятие об энтальпии газа. Основные уравнения первого закона термодинамики (2.3) и (2.4) были выведены для процессов, в которых работа расширения газа затрачивалась на преодоление внешних сил и была равна их работе.
Изменение кинетической энергии газа при расширении не учитывалось ввиду его незначительности. Такое расширение происходит, например, в поршневых двигателях внутреннего сгорания.
В турбинах, реактивных двигателях и других установках, в которых газ перемещается с большой скоростью, пренебрегать изменением кинетической энергии движущихся масс газа нельзя, так как оно является основным слагаемым в энергетическом балансе рабочего тела, и поэтому уравнения первого закона термодинамики (2.3) и (2.4) в этом случае принимают иной вид. Предположим, что по каналу переменного сечения под действием давления движется поток газа (рис. 2.2).
При этом будем считать, что:
1) движение газа по каналу установившееся и неразрывное. Это означает, что расход массы газа 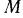 в единицу времени будет постоянным для любого сечения канала и для любого момента времени:
в единицу времени будет постоянным для любого сечения канала и для любого момента времени:
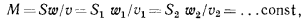
где 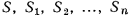 — площади отдельных поперечных сечений канала;
— площади отдельных поперечных сечений канала; 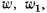
 —скорости газа в рассматриваемых поперечных сечениях;
—скорости газа в рассматриваемых поперечных сечениях; 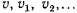
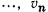 — соответствующие удельные объемы газа;
— соответствующие удельные объемы газа;
2) скорости по сечению, перпендикулярному оси канала, постоянны. Это допущение равносильно тому, что в каждом сечении берется средняя по расходу скорость;
3) трением частичек газа одна о другую и о стенки канала пренебрегаем;
4) поток газа при своем перемещении технической работы не совершает;
5) изменение параметров от сечения 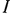 к сечению
к сечению 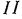 мало по сравнению с абсолютными их значениями.
мало по сравнению с абсолютными их значениями.
Очевидно, что количество подводимой теплоты 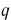 к 1 кг газа на участке между двумя произвольно выбранными сечениями
к 1 кг газа на участке между двумя произвольно выбранными сечениями 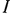 —
— 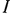 и
и 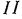 —
—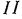 будет расходоваться на изменение внутренней энергии
будет расходоваться на изменение внутренней энергии 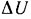 , на совершение газом работы (называемой здесь работой проталкивания) против внешних сил
, на совершение газом работы (называемой здесь работой проталкивания) против внешних сил 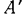 и на приращение кинетической энергии газа
и на приращение кинетической энергии газа 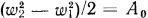 , т. е.
, т. е.
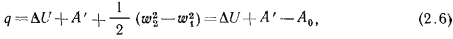
а в дифференциальной форме
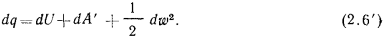
Уравнения (2.6) и (2.6′) являются математическим выражением первого закона термодинамики для газового потока.
Для определения работы проталкивания рассмотрим газ, находящийся между сечениями  и
и 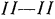 . На выделенный объем газа действуют массы газов, находящихся слева и справа от сечений
. На выделенный объем газа действуют массы газов, находящихся слева и справа от сечений 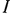 и
и 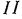 . Воздействие этих масс заменяем соответствующими силами, приложенными в указанных сечениях. В сечении
. Воздействие этих масс заменяем соответствующими силами, приложенными в указанных сечениях. В сечении  будет действовать сила
будет действовать сила 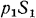 , а работа, совершаемая в единицу времени этой силой, составит
, а работа, совершаемая в единицу времени этой силой, составит 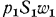 .
.
Поскольку работа производится внешними по отношению к выделенному объему газа силами, то, согласно принятым обозначениям, ее нужно считать отрицательной. В свою очередь выделенный объем газа сам совершит положительную работу по проталкиванию лежащих впереди слоев в сечении 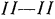 , равную
, равную 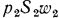 . Тогда, принимая во внимание знаки работ, работу проталкивания при перемещении 1 кг газа можно определить по уравнению
. Тогда, принимая во внимание знаки работ, работу проталкивания при перемещении 1 кг газа можно определить по уравнению 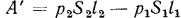 , где
, где 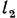 и
и 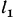 — пути, пройденные сечениями
— пути, пройденные сечениями 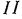 и
и 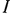 в 1 с;
в 1 с; 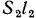 и
и 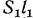 — секундные объемы 1 кг газа
— секундные объемы 1 кг газа 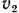 и
и 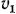 .
.
Тогда

или

Из уравнений (2.7) и (2.7′) следует, что работа проталкивания 1 кг газа представляет собой функцию только состояния газа, так как она не зависит от направления процесса и зависит лишь от начального и конечного состояний газа.
Подставляя выражение для 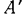 из уравнения (2.7) в уравнение (2.6), получим
из уравнения (2.7) в уравнение (2.6), получим
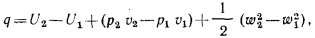
или
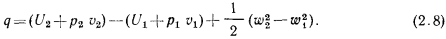
Выражение 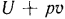 , входящее в это уравнение, является параметром состояния газа, поскольку
, входящее в это уравнение, является параметром состояния газа, поскольку 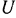 и
и 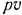 для каждого состояния газа имеют вполне определенные значения. Сумму
для каждого состояния газа имеют вполне определенные значения. Сумму 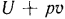 называют энтальпией газа и обозначают буквой
называют энтальпией газа и обозначают буквой 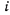 Энтальпия
Энтальпия 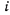 , так же как и
, так же как и 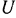 , измеряется в Дж/кг. Следовательно,
, измеряется в Дж/кг. Следовательно,
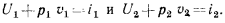
Тогда уравнение (2.8) примет вид
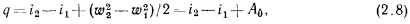
а в дифференциальной форме

Уравнения (2.8) и (2.9) наряду с уравнениями (2.6) и (2.6′) также являются аналитическими выражениями первого закона термодинамики в применении к газовому потоку и показывают, что теплота, сообщаемая движущемуся газу, расходуется на увеличение его энтальпии и внешней кинетической энергии.
В общем случае поток газа при своем перемещении может совершать и другие виды работ (например, вращать колесо турбины), которые называются техническими и обозначаются 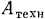 .
.
Техническая работа может не только отбираться от потока, но и подводиться к потоку (например, поток может нагнетаться центробежным вентилятором). Составной частью работы потока является также работа по преодолению сил трения на стенках канала 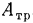 . С учетом этого уравнение (2.9) примет вид
. С учетом этого уравнение (2.9) примет вид
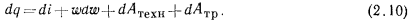
По своему существу уравнения (2.4) и (2.10) идентичны — они выражают первый закон термодинамики. Приравнивая правые части этих уравнений, получим
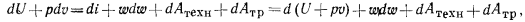
или
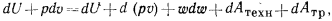
т. е.
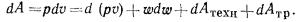
Таким образом, за счет работы расширения газа, движущегося в потоке 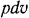 , осуществляются работы, расходуемые на проталкивание потока
, осуществляются работы, расходуемые на проталкивание потока 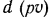 , изменение кинетической энергии потока
, изменение кинетической энергии потока 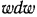 , техническая работа
, техническая работа 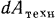 и работа по преодолению сил трения
и работа по преодолению сил трения 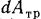 .
.
Если поток газа не совершает технической работы 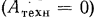 , то
, то 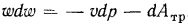 .
.
Для течения потока газа без трения 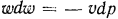 это важное соотношение используется при рассмотрении процессов истечения газа.
это важное соотношение используется при рассмотрении процессов истечения газа.
Следует отметить, что введение понятия «энтальпия газа» в значительной мере упрощает расчеты многих термодинамических процессов, вид и структуру некоторых формул и позволяет использовать графический метод исследования процессов, что исключительно широко применяется, особенно при расчете процессов изменения состояния водяного пара.
Остальные темы тут, они вам помогут подробнее понять термодинамику!
Как параметр состояния газа энтальпия является функцией любых независимых переменных (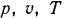 ), определяющих его состояние, т. е.:
), определяющих его состояние, т. е.: