Оглавление:

Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «сопротивление материалов».
Лекции подготовлены для студентов любых специальностей и охватывает полный курс предмета «сопротивление материалов».
В лекциях вы найдёте основные законы, теоремы, формулы и примеры задач с подробным решением.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Сопротивление материалов (разг. — сопромат) — это наука о прочности и надёжности деталей машин и конструкций. В её задачи входит обобщение инженерного опыта создания машин и сооружений, разработка научных основ проектирования и конструирования надёжных изделий, совершенствование методов оценки прочности. Является частью механики деформируемого твёрдого тела, которая рассматривает методы инженерных расчётов конструкций на прочность, жесткость и устойчивость при одновременном удовлетворении требований надежности, экономичности и долговечности. wikipedia.org/wiki/Сопротивление_материалов
Введение в сопротивление материалов
Все науки, изучающие поведение твёрдых тел, объединены в одно научное направление, которое называется механикой твердого деформируемого тела. Самой общей наукой этого направления, в которой изучается поведение не только твердых, но и газообразных и жидких тел, является реология. Механика твердого тела включает основные разделы: теоретическая механика; сопротивление материалов; строительная механика; линейная (классическая) теория упругости; нелинейная теория упругости; теория пластичности; теория ползучести; теория упругости анизотропного тела; теория упругости неоднородного тела и др.
Теоретическая механика — это наука изучающая взаимодействие абсолютно твердых тел и их движение. Появление внутренних сил и их распределение внутри твердых деформируемых тел не рассматривается.
Сопротивление материалов — это инженерная дисциплина изучает распределение внутренних сил в прямых (или кривых) брусьях. В основу исследований положена гипотеза плоских сечений. Изучаются вопросы прочности материалов при различных воздействиях на строительные конструкции, детали машин и механизмов.
Строительная механика (классическая) — занимается определением внутренних сил в сложных стержневых системах. В специальных разделах строительной механики изучаются пластины, оболочки, арки и др.
Линейная (классическая) теория упругости — изучает деформации и напряжения в линейно упругих телах: толстых брусьях, пластинах, оболочках, массивах. Линейная теория упругости основывается на предположении об идеальной упругости тела и законе Гука. В отличие от сопротивления материалов гипотеза плоских сечений не принимается.
Нелинейная теория упругости — изучает деформации и напряжения в телах с нелинейной диаграммой деформирования материала. При этом закон деформирования должен быть обратимым.
Теория пластичности — изучает деформацию тел, имеющих нелинейную диаграмму деформирования. При этом процесс деформирования может быть необратим.
Теория ползучести — изучает изменение деформаций и напряжений во времени в результате начального нагружения тела
Самой сложной наукой в механике твердого тела является реология.
Реология — это наука, устанавливающая общие закономерности образования и развития во времени деформаций любого вещества от различных причин и в различных термодинамических и физико-химических условиях.
Предметом исследования в сопротивлении материалов является брус (прямолинейные и криволинейные, постоянного и переменного сечений стержни).
Задачей сопротивления материалов и других родственных дисциплин является создание прочных, устойчивых, долговечных и экономически выгодных сооружений и механизмов.
История развития сопротивления материалов (науки о прочности)
Создание прочных, надежных конструкций издавна интересует человечество. Используя метод проб и ошибок, а также, заимствуя некоторые решения у природы, были достигнуты значительные практические успехи. Вместе с тем, этот путь был отмечен техническими катастрофами и гибелью людей.
Историческим началом науки о прочности принято считать пятнадцатое столетие. Век Великих Географических открытий был ознаменован бурным развитием кораблестроения, военной техники и астрономии. Это, в свою очередь, вызвало необходимость решения многих задач прочности. Так, известно, что Леонардо да Винчи занимался испытанием канатов на прочность и пытался решить задачу о прочности балок.
Однако, поскольку Леонардо никогда не публиковал своих работ, основателем сопротивления материалов как науки считается Галилео Галилей, который занимался испытанием деревянных балок на изгиб и написал об этом книгу.
Большой вклад в развитие науки о прочности внесло открытие интегрального и дифференциального исчисления Ньютоном и Лейбницем.
В 1676 году английский ученый Роберт Гук опубликовал закон деформирования упругих тел (каково удлинение, такова сила), являющийся основным законом сопротивления материалов.
В 1809 году Томас Юнг ввел понятие модуля упругости, а в 1822 Огюстен Луи Коши ввел понятие напряжения. Это дало возможность записать закон Гука в современном виде.
В 1829 году французский инженер и ученый Анри Навье издал первое руководство по сопротивлению материалов.
Дальнейшее развитие этой науки было вызвано бурным развитием промышленности и транспорта и связано с трудами таких ученых, как Эйлера, Кастилиано, Максвелла, Кулона, Мора, Журавского, Ясинского и др. Первый учебник «Сопротивление материалов» был написан великим русским ученым и инженером С.П . Тимошенко.
Внешние силы и их классификация
Характер приложения нагрузки (статические, динамические, вибрационные, мгновенно приложенные нагрузки) оказывают
существенное влияние на прочность и долговечность строительных конструкций. Поэтому оценке характера нагрузки следует придавать большое значение. Для того, чтобы такую оценку упростить нагрузку классифицируют.
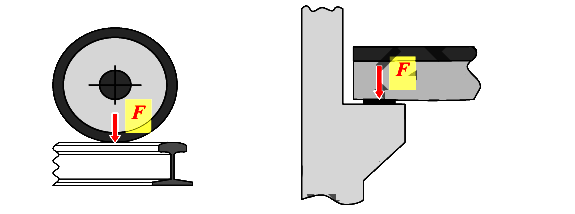
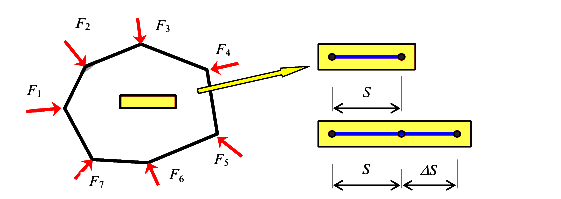
Сосредоточенные силы — это нагрузки, передающиеся на тело через площадку, размеры которой несравнимо малы по сравнению с размерами самого тела. Обозначается буквой F. Имеет размерность Н, кН.
Пример №1
Действие колеса локомотива на рельс, действие балки на консоль колонны (рис.1) и пр.
Распределенные нагрузки — это нагрузки, передающиеся на тело через площадки, размеры которых сравнимы с размерами самого тела.
Если нагрузка распределена по площади, то она обозначается обычно буквой р и имеет размерность 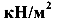 если нагрузка распределена по линии, то она обозначается буквой q и имеет размерность кН/м.
если нагрузка распределена по линии, то она обозначается буквой q и имеет размерность кН/м.
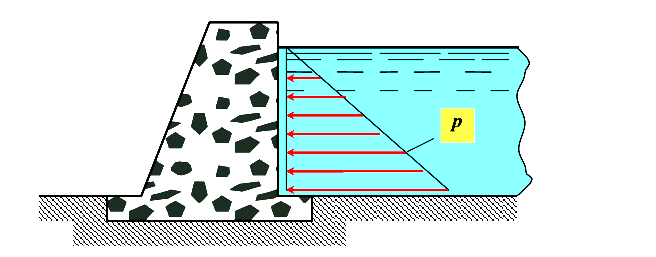
Пример №2
Действие напора воды на дамбу (рис.2).
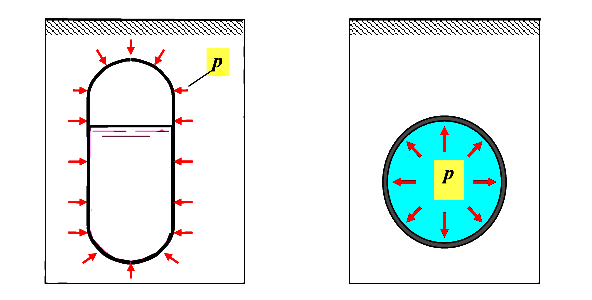
Поверхностные силы — это силы, возникающие в результате взаимодействия двух тел: твердого и твердого; твердого и жидкого; твердого и газообразного и приложены к их поверхностям.
Примеры поверхностных сил приведены на рисунке 3.
Объемные силы — это силы, возникающие в результате взаимодействия полей (гравитационного (собственный вес), силы инерции, центробежные силы, электромагнитные силы и пр.). Эти силы распределены по всему или по части объема тела. Размерность таких нагрузок — 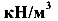
Пример №3 Действие сил на якорь электродвигателя, вес водонапорной башни, силы инерции при начале движения автомобиля и пр.
Постоянные нагрузки — это нагрузки, действующие на сооружение на протяжении всего срока службы самого сооружения.
Пример №4 Собственный вес сооружения.
Временные нагрузки — это нагрузки, действующие ограниченный срок, меньший, чем срок службы самого сооружения.
Пример №5 Нагрузка на кровлю от веса снега, нагрузка от давления ветра, нагрузка от технологического оборудования и др.
Статическая нагрузка — это нагрузка, изменяющаяся во времени настолько медленно, что ускорениями точек конструкции, а, следовательно, и силами инерции можно пренебречь.
Пример №6 Собственный вес конструкции, нагрузка от веса снега и др.
Динамические нагрузки — это нагрузки, изменяющие свою величину или положение достаточно быстро. Поэтому силами инерции пренебречь нельзя, так как они соизмеримы с силами, вызванными статическими нагрузками.
Пример №7 Движение мостового крана, действие кузнечного молота на заготовку, забивка свай и др.
Вид нагрузки устанавливается исходя из субъективных предпосылок конструктора или в соответствии с нормами проектирования при выборе расчетной схемы строительной конструкции.
Типы элементов строительных сооружений
Элементы сооружений по своей геометрической форме делятся на четыре типа — брус, пластина, оболочка и массив.
Брус — тело, у которого два основных размера малы по сравнению с третьим размером (рис.4)
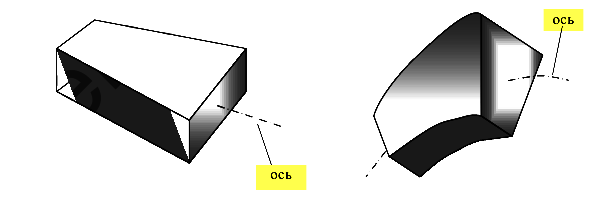
Осью бруса называется линия, соединяющая центры тяжестей всех поперечных сечений. Брус с прямолинейной осью называется стержнем.
Пример №1 Балки, стойки рам, колонны.
Пластина (пластинка) — это тело, ограниченное двумя плоскими поверхностями, расстояние между которыми мало по сравнению с прочими размерами (рис.5).
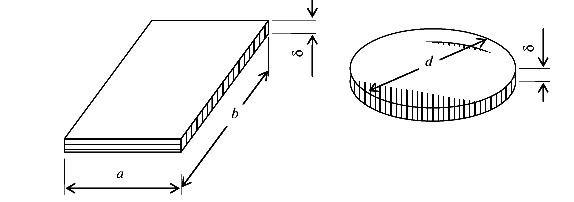
Пластины различаются по своей форме — прямоугольные, треугольные, круглые, эллиптические и др.
Оболочка — это тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с прочими (генеральными) размеры (рис.6, а)
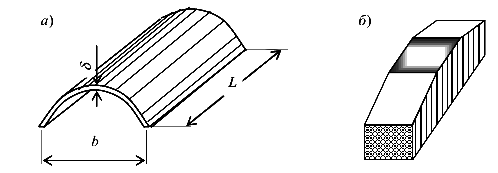
Оболочки различаются своей формой кривизны — цилиндрические, сферические, гауссовой кривизны и др.
Массив — это тело, у которого все три основные размеры одного порядка (рис.6, 6).
Основные гипотезы (допущении) в сопротивлении материалов
Как и во всякой науке в сопротивлении материалов реальная природа рассматривается односторонне и идеализируется. Это достигается введением понятий, принятием гипотез и допущений.
1.Материал тела имеет сплошное (непрерывное) строения, то есть не принимается во внимание дискретное, атомарное строение вещества.
2.Материал элемента конструкции однороден, то есть во всех его точках механические свойства одинаковые.
3.Материал тела изотропен, то есть в любой его точке по всем направлениям механические свойства совершенно одинаковые. У анизотропных тел, например, у древесины механические свойства по разным направлениям разные. Под механическими свойствами следует понимать прочность или жесткость. Отметим, что прочность древесины вдоль волокон значительно (в два три раза) больше чем прочность поперек волокон (рис.7).
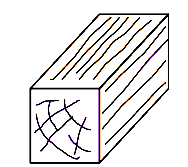
Рис. 7. Пример анизотропного материала (древесины)
4. В твердом теле до приложения нагрузки внутренние начальные силы отсутствуют. В действительности в элементах строительных конструкций или сооружения всегда имеются начальные внутренние силы, которые могут быть вызваны;
- неравномерным остыванием;
- неравномерной усадкой;
- неравномерным высушиванием;
- механической обработкой.
5.Принцип суперпозиций или принцип независимости действия сил. Результат действия на тело системы сил равен сумме результатов действия тех же сил, прикладываемых к телу последовательно и в любом порядке. Принцип независимости действия сил справедлив при соблюдении двух условий:
а) геометрической линейности — перемещения точек механической системы, вызванные деформацией, малы по сравнению с ее размерами;
б) физической линейности — перемещения, являющиеся результатом деформации системы, линейно зависят от нагрузки (то есть, если выполняется закон Гука).
6. Принцип Сен-Венана — в точках тела, достаточно далеко удаленных от места приложения нагрузки, величина внутренней силы весьма мало зависит от способа приложения нагрузки. А примером может служить разрезание стального листа ножницами (рис.8).
ножницами)
Понятие о деформациях
Изменение формы или размеров тела, вызванное нагрузкой, изменением температуры или другими воздействиями называется деформацией.
Деформация делится на два вида — линейные и угловые.
Изменение линейных размеров тела называется линейной деформацией. Линейную деформация тела разделяют на абсолютную 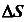 и относительную линейную
и относительную линейную 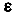 деформации.
деформации.
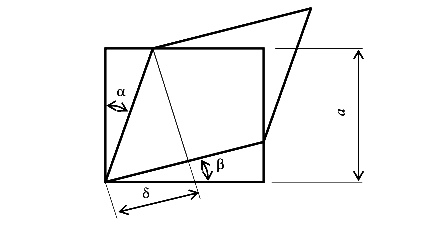
Относительная линейная деформация в точке тела равна пределу отношения абсолютной деформации отрезка волокна к длине отрезка, если длина отрезка стремится к нулю

где S — длина отрезка волокна; 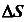 деформация (удлинение или укорочение) отрезка волокна (рис.9)
деформация (удлинение или укорочение) отрезка волокна (рис.9)
Изменение угловых размеров тела (рис.10) называется угловой деформацией.

где 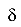 — абсолютная угловая деформация (обычно не употребляется в расчетах);
— абсолютная угловая деформация (обычно не употребляется в расчетах);
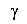 — относительная угловая деформация (угол сдвига), величина безразмерная.
— относительная угловая деформация (угол сдвига), величина безразмерная.
Основные свойства твердого деформируемого тела
Все материалы в сопротивлении материалов характеризуются тремя основными свойствами — упругость, пластичность и ползучесть.
Деформации, полностью исчезающие после разгрузки тела, называются упругими деформациями.
Свойства тела восстанавливать после разгрузки свою первоначальную форму и размеры называется упругостью.
Деформации, сохраняемые телом после снятия нагрузки, называются остаточными (пластическими) деформациями.
Свойство материала давать остаточные деформации называется пластичностью материала.
Для некоторых материалов при определенных условиях наблюдаются деформации во времени. Свойства таких материалов изучается теорией ползучести. В теории ползучести выделяют два понятия: релаксация и ползучесть.
Явление увеличения деформаций во времени при постоянной нагрузке называется ползучестью.
Явление уменьшения напряжений во времени при постоянной деформации называется релаксацией.
Пластичность материала проявляется обычно при больших механических напряжениях, а ползучесть — при большой температуре.
Внешние и внутренние силы. Метод сечений
В сопротивлении материалов различают внешние и внутренние силы.
Внешние силы — это силы взаимодействия между отдельными телами.
Внутренние силы — это силы взаимодействия между частями одного и того же тела.
Внутренние силы передаются через межатомарные или межмолекулярные связи, которые всегда присутствуют в твердых телах.
Разрушение тел происходит за счет внутренних сил. Поэтому одной из главных задач сопротивления материалов является определение внутренних сил в конструкциях.
Для определения внутренних сил используется метод сечений. Суть метода сечений состоит в следующем.
1) Тело мысленно разделяется на две части в том месте, где требуется определить внутренние силы.
2) Одна часть вместе с приложенными к ней внешними силами, отбрасывается, а к оставшейся части, кроме приложенных к ней внешних сил, прикладываются внутренние силы, то есть силы действия отброшенной части на оставшуюся.
3) Считается, что оставшаяся часть вместе с приложенными к ней внутренними и внешними силами находится в состоянии равновесия. Используя уравнения равновесия, определяют внутренние силы.
4) По законам теоретической механики система внешних сил, приложенных к рассматриваемой части, приводится к главному вектору сил Р и главному вектору момента М. Так как рассмотренная часть находится в состоянии равновесия, то главные вектора Р и М внешних сил должны быть равны главным векторам силы и момента внутренних сил.
5) Главные вектора внутренних сил можно разложить на составляющие
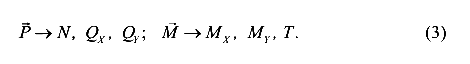
6) Для определения составляющих внутренних сил используются уравнения равновесия рассматриваемой части стержня (4).
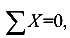 определяется составляющая
определяется составляющая 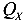 ;
;
2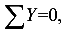 , определяется составляющая
, определяется составляющая 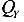 ;
;
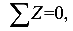 определяется составляющая N;
определяется составляющая N;
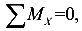 определяется составляющая
определяется составляющая 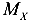 ;
;
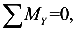 определяется составляющая
определяется составляющая 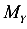 ;
;
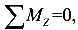 определяется составляющая Т.
определяется составляющая Т.
Отметим, что каждое уравнение содержит только одну составляющую внутренних сил, Поэтому для их определения даже не приходиться решать систему уравнений.
Дадим определения.
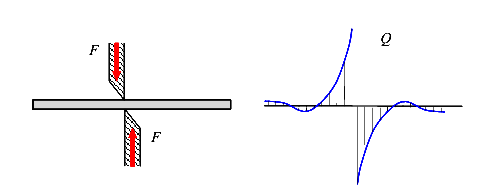
Продольная сила (N, кН) — это внутренняя сила численно равная сумме проекций всех внешних сил, приложенных по одну сторону от сечения, на продольную ось стержня.
Поперечная сила (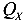 или Q, кН) — это внутренняя сила, численно равная сумме проекций всех внешних сил, приложенных по одну сторону от сечения, на соответствующую поперечную ось X или Y.
или Q, кН) — это внутренняя сила, численно равная сумме проекций всех внешних сил, приложенных по одну сторону от сечения, на соответствующую поперечную ось X или Y.
Крутящий момент (Т, кНм) — это внутренняя сила, численно равная сумме моментов всех внешних сил, приложенных по одну сторону от сечения, относительно продольной оси стержня.
Изгибающий момент 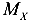 или
или 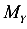 кНм) — это внутренняя сила, численно равная сумме моментов всех внешних сил, приложенных по одну сторону от сечения, относительно соответствующей поперечной оси X или Y, проходящей через центр тяжести этого сечения.
кНм) — это внутренняя сила, численно равная сумме моментов всех внешних сил, приложенных по одну сторону от сечения, относительно соответствующей поперечной оси X или Y, проходящей через центр тяжести этого сечения.
Виды простых деформаций (сопротивлений) бруса
В сопротивлении материалов различают четыре вида простых сопротивлений бруса.
1 .Центральное растяжение (сжатие) — вид сопротивления, при котором во всех поперечных сечениях участка стержня появляются только продольные силы N. Пример центрально сжатой колонны приведен на рисунке (рис. 11, а).
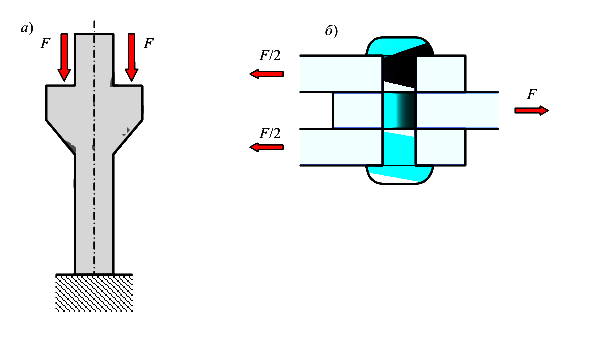
2.Сдвиг (срез) — вид сопротивления, при котором в поперечных сечениях появляются только поперечные силы 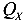 или
или 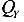 . Действие среза испытывают стержни заклепки (рис. 11,6)
. Действие среза испытывают стержни заклепки (рис. 11,6)
3.Кручение — вид сопротивления, при котором во всех поперечных сечениях участка стержня появляются только крутящие моменты Т.
Примеры: Работа вала машины (механизма), иногда элементов пространственных конструкций. Чистый сдвиг можно также получить и при кручении тонкостенной трубки.
4.Чистый изгиб — это такой вид сопротивления, при котором во всех поперечных сечениях участка стержня появляются только изгибающие моменты 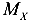 х или
х или 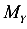 .
.
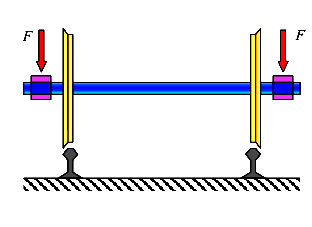
1.1.10. Понятие о напряжениях
Внутренние силы N, 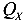 ,
, 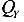 ,
, 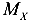 ,
,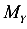 и Т в поперечном сечении стержня в действительности не являются сосредоточенными силами. Они распределены по площади сечения по некоторым законам. Определение этих законов является одной из основных задач сопротивления материалов.
и Т в поперечном сечении стержня в действительности не являются сосредоточенными силами. Они распределены по площади сечения по некоторым законам. Определение этих законов является одной из основных задач сопротивления материалов.
Распределение внутренних сил характеризуется их интенсивностью, которая измеряется напряжениями (механическими напряжениями). Введем понятие о напряжениях. Рассмотрим поперечное сечение стержня и напряжения в его точке.
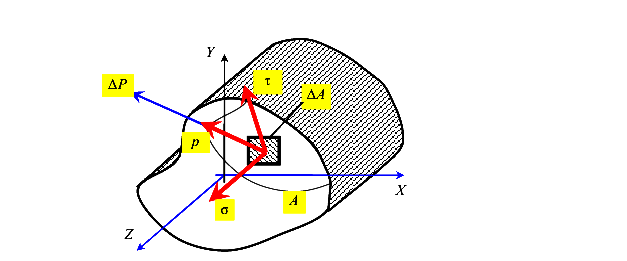
Около произвольной точки выделим малую площадку 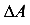 , через которую передается малая внутренняя сила
, через которую передается малая внутренняя сила 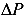 (рис.13).
(рис.13).
Полным напряжением р (МПа) в точке называется величина, характеризующая интенсивность внутренней силы, равная пределу отношения внутренней силы 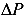 , передающейся через площадку
, передающейся через площадку 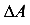 , если площадь
, если площадь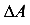 площадки стремится к нулю
площадки стремится к нулю

В расчетах полное напряжение редко используется. Обычно используются нормальное и касательное напряжения.
Нормальным напряжением 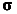 (МПа) в точке называется величина, равная проекции полного напряжения на нормаль рассматриваемой площадки. Если нормальное напряжение вызывает сжатие, то оно считается отрицательным, если вызывает растяжение — принимается положительным.
(МПа) в точке называется величина, равная проекции полного напряжения на нормаль рассматриваемой площадки. Если нормальное напряжение вызывает сжатие, то оно считается отрицательным, если вызывает растяжение — принимается положительным.
Касательным напряжением 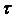 (МПа) в точке называется величина, равная проекции полного напряжения на плоскость рассматриваемой площадки. Правило расстановки знаков для касательного напряжения будет рассмотрено позже.
(МПа) в точке называется величина, равная проекции полного напряжения на плоскость рассматриваемой площадки. Правило расстановки знаков для касательного напряжения будет рассмотрено позже.
Такое разложение полного напряжения на нормальное и касательное сложилось исторически и вполне обосновано. Опыты показывают, что материалы по-разному сопротивляются растяжению (сжатию) и сдвигу.
Связь напряжений и внутренних сил
Для исследований характера распределения внутренних сил по площади сечения установим связь между внутренними силами и напряжениями. Полагаем, что распределение напряжений в пределах сечения выражается непрерывными функциями (рис.14).
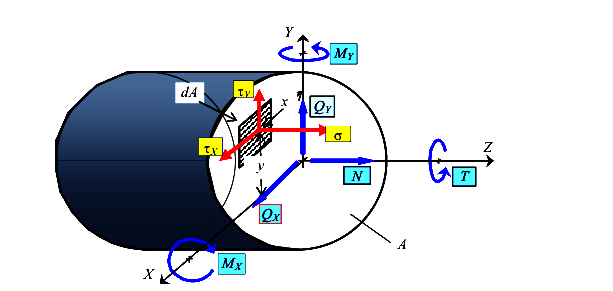
Элементарная продольная сила, передающаяся через площадку dA равна

Предполагается, что в пределах элементарной площадки из-за ее малости напряжения 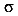 распределены равномерно. Проинтегрируем левую и правую части записанного выражения (6) и получим
распределены равномерно. Проинтегрируем левую и правую части записанного выражения (6) и получим

Элементарный момент относительно оси X, вызванный элементарной силой 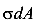 , передающейся через площадку dA, равен
, передающейся через площадку dA, равен
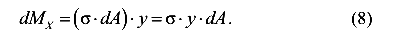
Проинтегрируем левую и правую части выражения (8) и получим

Остальные четыре связи напряжений и внутренних сил рекомендуется получить самостоятельно.
Центральное растяжение (сжатие)
Общие понятия. Определение продольных сил при центральном растяжении (сжатии)
Центральное растяжение (сжатие) появляется в тросе при буксировке или подъеме груза, в колоннах промышленных и гражданских зданий и пр.
Для удобства условимся всегда продольную ось обозначать буквой Z, а поперечные оси, то есть оси расположенные в плоскости поперечного сечения, буквами X и Y.
Центральное растяжение (сжатие) — это такой вид сопротивления, при котором в поперечных сечениях стержня появляются только продольные силы.
Продольная сила принимается положительной, если она вызывает растяжение материала или отрицательной — если сжатие.
В тех случаях, когда знак продольной силы неизвестен заранее, ее следует принимать положительной. В результате расчета знак силы уточняется.
Для вычисления продольной силы используется метод сечений.
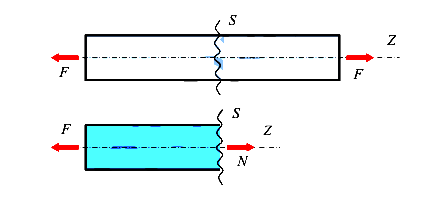
Разделим стержень, показанный на рисунке 15, поперечным сечением S на две части — левую и правую. Отбросим правую часть и рассмотрим левую часть с левой силой F и продольной силой N, которую прикладываем так, чтобы она растягивала материал оставшейся левой части стержня, то есть была положительной. Составим уравнение равновесия оставленной левой части стержня, которое будет содержать силу F и продольную, силу N
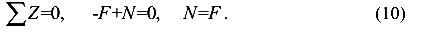
Решение уравнения (10) дает положительное значение продольной силы Nчто подтверждает предположение о том, что продольная сила растягивающая.
В последствие будем полагать, что нагрузка, какая бы она не была, всегда положительная, а ее действие определяется направлением.
Эпюрой продольной силы N называется график, каждая ордината которого равна значению продольной силы в данном сечении. Эпюры и не только продольных сил отличаются от других графиков тем, что они построены по специальным правилам.
Основные правила построения эпюр:
- ординаты откладываются перпендикулярно к линии отсчета;
- эпюры всегда строятся в удобном масштабе и так, чтобы они легко читались, то есть без наложений и без затенения самой конструкции;
- значения подписываются без указания знака и размерностей;
- знаки проставляются на знаковых полях эпюры обычно в кружочках;
- вся эпюра подписывается наименованием той величины, для которой она построена, и там же указывается размерность этой величины.
Дифференциальная зависимость между продольной силой и нагрузкой
Пусть дан стержень (рис.16), загруженный распределенной по некоторому закону нагрузкой q(z)
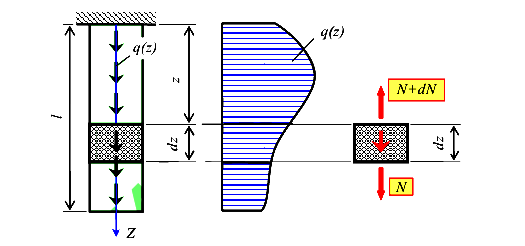
Рассмотрим элементарный участок стержня длиной dz. Учитывая условие равновесия
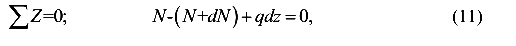
получим
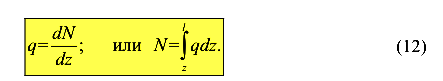
Таким образом, производная от продольной силы N равна интенсивности распределенной нагрузки q. Полученная зависимость
используется для проверки эпюры N, а так же для вывода некоторых формул.
Напряжения в поперечном сечении бруса при центральном растяжении (сжатии)
Рассмотрим длинный стержень, испытывающий центральное растяжение, (рис.17).
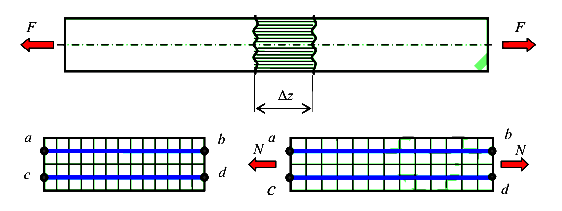
Опыты показывают, что сечение b-d в результате деформации выделенного участка стержня переместиться параллельно само себе, оставаясь при этом плоским. Это означает, что волокна а-Ь и c-d удлиняются одинаково. Отсюда следует утверждение.
Гипотеза Бернулли (гипотеза плоских сечений). Поперечные сечения плоские до деформации остаются плоскими и после деформации.
На основании гипотезы Бернулли все продольные волокна стержня деформируются одинаково. Следовательно, напряжения в них также одинаковые, а значит напряжения и по всей площади поперечного сечения распределены равномерно.
Опыты показывают, что сечение b-d в результате деформации выделенного участка стержня переместиться параллельно само себе, оставаясь при этом плоским. Это означает, что волокна а-Ь и c-d удлиняются одинаково. Отсюда следует утверждение.
Гипотеза Бернулли (гипотеза плоских сечений). Поперечные сечения плоские до деформации остаются плоскими и после деформации.
На основании гипотезы Бернулли все продольные волокна стержня деформируются одинаково. Следовательно, напряжения в них также одинаковые, а значит напряжения и по всей площади поперечного сечения распределены равномерно.

Используя зависимость (7) между напряжениями о и продольной силой N, получим
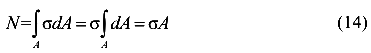
или

Здесь N — продольная сила в поперечном сечении стержня; А -площадь поперечного сечения.
Напряжения в наклонном сечении стержня при центральном растяжении (сжатии)
Рассмотрим длинный центрально растянутый стержень. В средней части стержня проведем сечение под углом а к поперечному сечению
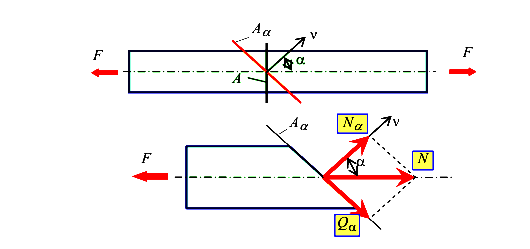
На рисунке 18 отмечены А — площадь поперечного сечения; 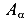 -площадь наклонного сечения;
-площадь наклонного сечения; 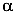 — угол наклона сечения; N- продольная сила в растянутом стержне;
— угол наклона сечения; N- продольная сила в растянутом стержне; 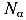 — нормальная сила в наклонном сечении;
— нормальная сила в наклонном сечении; 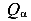 -поперечная (сдвигающая) сила в наклонном сечении.
-поперечная (сдвигающая) сила в наклонном сечении.
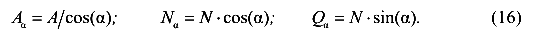
Отсюда выразим нормальное напряжение
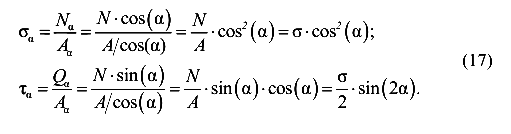
Окончательно имеем

Здесь 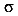 — нормальное напряжение в поперечном сечении стержня. Проведем анализ напряженного состояния стержня:
— нормальное напряжение в поперечном сечении стержня. Проведем анализ напряженного состояния стержня:
Очевидно, что максимальные нормальные напряжения появляются при а=0° , то есть в поперечном сечении стержня. Максимальные касательные напряжения появляются в наклонном под углом  сечении и равны половине нормального напряжения.
сечении и равны половине нормального напряжения.
Продольные и поперечные деформации центрально растянутого (сжатого) бруса. Закон Гука
Рассмотрим длинный стержень, подвергнутый центральному растяжению (рис.19)
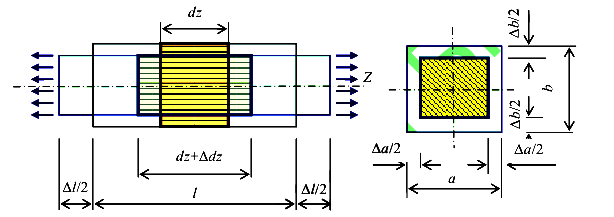
Согласно определению относительная продольная деформация волокна равна

Здесь длина волокна S равна длине элементарного участка dS. Поэтому

Предел не записывается, потому что дифференциал dz и так стремится к нулю. Из полученной формулы следует

Согласно гипотезе Бернулли все волокна находятся в одинаковых условиях. Кроме того, будем полагать, что по всей своей длине волокна
деформируются одинаково, так как рассматривается длинный стержень. Поэтому 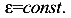
Проинтегрируем (то есть просуммируем) деформации по длине волокна и получим
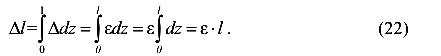
Окончательно имеем

Аналогичные рассуждения для поперечных деформаций приводят к выражениям
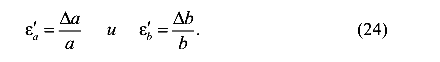
Если материал изотропен, то

Отношение относительной поперечной деформации к относительной продольной деформации, взятое по абсолютной величине называется коэффициентом поперечной деформации или коэффициентом Пуассона.

Здесь 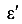 — относительная линейная поперечная деформация, то есть деформация по направлению перпендикулярному к направлению действия силы или нормального напряжения;
— относительная линейная поперечная деформация, то есть деформация по направлению перпендикулярному к направлению действия силы или нормального напряжения;
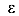 — относительная линейная продольная деформация, то есть деформация по направлению действия силы или нормального напряжения.
— относительная линейная продольная деформация, то есть деформация по направлению действия силы или нормального напряжения.
Коэффициент Пуассона v — величина безразмерная и теоретически для изотропных материалов может принимать значения

Если известен коэффициент Пуассона v, то, зная продольную деформацию, всегда можно найти поперечную деформацию

Продольная и поперечная деформации всегда имеют разные знаки.
Коэффициент Пуассона характеризует способность материала давать поперечные деформации.
Справка.

Закон Гука. Для некоторых материалов экспериментально установлено, что до некоторого предела деформации изменяются упруго и прямо пропорционально напряжениям.

Здесь Е — модуль упругости первого рода или просто модуль упругости, измеряется в Па, МПа, ГПа.
Справка.

Модуль упругости характеризует жесткость материала, то есть является мерой сопротивления материала продольному деформированию.
Физические коэффициенты Е и v могут быть найдены только испытанием материала.
Деформация 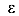 и
и 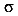 — относительные величины
— относительные величины

Подставим их в закон Гука (29)

Отсюда имеем закон Гука при центральном растяжении (сжатии) в абсолютных величинах

где N— продольная сила на рассматриваемом участке стержня;
l — длина участка стержня;
Е — модуль упругости материала стержня;
А — площадь поперечного сечения на рассматриваемом участке стержня.
Полученная формула справедлива, если стержень на рассматриваемом участке постоянного сечения и продольная сила во всех его поперечных сечениях постоянная.
Величина ЕА называется жесткостью стержня при центральном растяжении (сжатии).
Перемещения сечений бруса
Перемещение (смещение) сечения бруса равно деформации части бруса, расположенной между защемлением (опорой) и рассматриваемым сечением.
Перемещения, совпадающие с положительным направлением продольной оси Z, считаются положительными.
Если начало координат всегда располагать в защемлении бруса, а ось Z направлять в сторону самого бруса, то знак перемещения будет совпадать со знаком суммы деформаций участков стержня, расположенных между защемлением и рассматриваемом сечении.
Особенности расчета плоских стержневых систем
Ограничимся рассмотрением механических систем, содержащих хотя бы один абсолютно жесткий (очень жесткий) и шарнирно прикрепленный к неподвижной опоре стержень (элемент). Это ограничение упрощает ее расчет. Кроме того, также для упрощения расчета сделаем следующие предположения:
- абсолютно жесткий стержень может только поворачиваться около неподвижного шарнира;
- все точки диска, за исключением точки в неподвижном шарнире, движутся по дугам окружностей с центром в неподвижном шарнире;
- перемещения точек диска малы по сравнению с размерами самого диска, поэтому для упрощения расчета принимаем, что точки движутся не по дугам окружностей, а по касательным к ним;
- считаем, что стержни системы деформируются по закону Гука;
- зависимости перемещений точек и радиусов, описываемых ими дуг, имеет вид

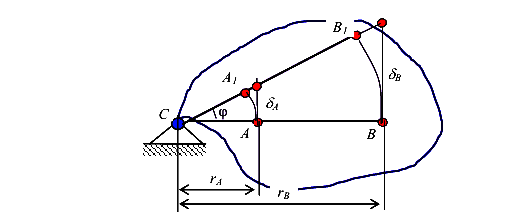
Здесь 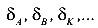 перемещения точек диска;
перемещения точек диска; 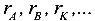 радиусы дуг, по которым движутся эти точки при повороте диска около неподвижного шарнира С (рис.20).
радиусы дуг, по которым движутся эти точки при повороте диска около неподвижного шарнира С (рис.20).
Деформация стержня от собственного веса
Рассмотрим стержень, загруженный собственным весом (рис. 21)
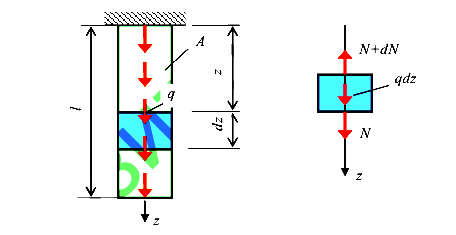
Пусть р — плотность материала; g — ускорение свободного падения; А — площадь поперечного сечения. В этом случае интенсивность распределенной нагрузки равна весу стержня длиной в один метр

Составим уравнение равновесия выделенного элементарного участка стержня
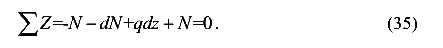
Отсюда имеем

Найдем продольную силу в выделенном сечении стержня. Эта продольная сила создается весом части стержня, расположенной ниже выделенного сечения. Для этого проинтегрируем левую и правую часть уравнения (36) на отрезке от l до z.
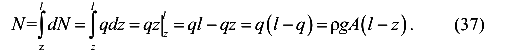
Окончательно имеем

Найдем нормальные напряжения, вызванные собственным весом
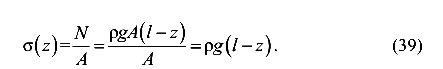
Имеем

Найдем деформации стержня от собственного веса. Вначале выразим относительную линейную деформацию
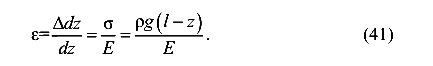
Отсюда получаем абсолютную деформацию элементарного участка стержня

Проинтегрируем левую и правую части выражения (42) по всей длине стержня
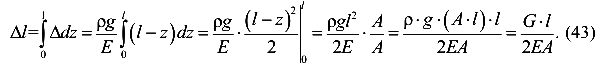
Окончательно имеем

Здесь G — вес стержня.
Возможно эта страница вам будет полезна:
| Сопромат — решение задач и примеров |
Механические характеристики материалов
Механические характеристики материалов делятся на две группы -характеристики прочности и характеристики пластичности.
Механические характеристики прочности
К механическим характеристикам прочности материалов относятся предел пропорциональности, предел текучести и предел прочности.
Пределом пропорциональности (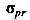 ,
, 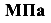 ) называется механическая характеристика прочности равная максимальному напряжению, до которого еще справедлив закон Гука.
) называется механическая характеристика прочности равная максимальному напряжению, до которого еще справедлив закон Гука.
Пределом текучести (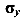 , МПа) называется механическая характеристика прочности равная напряжению, при котором происходят большие деформации без заметного изменения нагрузки.
, МПа) называется механическая характеристика прочности равная напряжению, при котором происходят большие деформации без заметного изменения нагрузки.
Пределом прочности (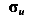 , МПа) называется механическая характеристика прочности равная отношению максимальной нагрузки, которую способен выдержать образец, к первоначальной площади поперечного сечения.
, МПа) называется механическая характеристика прочности равная отношению максимальной нагрузки, которую способен выдержать образец, к первоначальной площади поперечного сечения.
Обратите внимание, что предел прочности — это не напряжение, а условная величина, равная отношению максимальной нагрузки и первоначальной площади поперечного сечения, но обозначается она так же, как и напряжение буквой 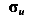 . Это объясняется тем, что при испытании площадь поперечного сечения может меняться, особенно у пластичных материалов. Однако при расчете элементов строительных конструкций изменение площади их поперечных сечений не учитывается. Поэтому для определения предела прочности приходиться силу относить к первоначальной площади поперечного сечения до испытания.
. Это объясняется тем, что при испытании площадь поперечного сечения может меняться, особенно у пластичных материалов. Однако при расчете элементов строительных конструкций изменение площади их поперечных сечений не учитывается. Поэтому для определения предела прочности приходиться силу относить к первоначальной площади поперечного сечения до испытания.
Иногда в качестве механических характеристик принимают касательные напряжения — 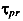 ,
, 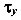 и
и 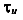 , если речь идет о сдвиге.
, если речь идет о сдвиге.
Механические характеристики пластичности
Обычно выделяют две основные характеристики пластичности материалов — это относительное остаточное удлинение 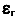 и относительное остаточное сужение
и относительное остаточное сужение 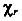 Выражаются эти характеристики в процентах.
Выражаются эти характеристики в процентах.
Относительным остаточным удлинением 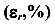 называется механическая характеристика пластичности равная отношению абсолютного остаточного удлинения к длине образца до испытания, выраженная в процентах
называется механическая характеристика пластичности равная отношению абсолютного остаточного удлинения к длине образца до испытания, выраженная в процентах

Относительным остаточным сужением 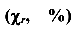 называется отношение разности площадей поперечного сечения до испытания и после испытания к площади сечения до испытания, выраженной в процентах.
называется отношение разности площадей поперечного сечения до испытания и после испытания к площади сечения до испытания, выраженной в процентах.

Методы расчета на прочность
В истории развития науки о прочности можно выделить три основных метода — это метод разрушающих нагрузок, метод допускаемых напряжений и метод предельных состояний.
Метод разрушающих нагрузок
В качестве условия прочности ставится требование, чтобы наибольшая нагрузка на сооружение не превышала некоторой допускаемой нагрузки 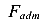 которая равна разрушающей (опасной) нагрузки, деленной на коэффициент запаса прочности
которая равна разрушающей (опасной) нагрузки, деленной на коэффициент запаса прочности

Коэффициент запаса прочности n принимается с учетом:
- разброса механических характеристик материала;
- отклонения величины нагрузок;
- качества и степени однородности материала;
- долговечности и назначения сооружения.
Разрушающая нагрузка при центральном растяжении (сжатии) для упругопластических материалов принимается с учетом диаграммы Прандтля (рис. 22).
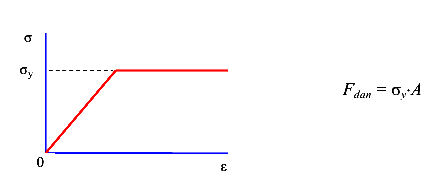
Разрушающая нагрузка при центральном растяжении (сжатии) для хрупких материалов вычисляется по формуле (48), а для упругопластических материалов по формуле (49)

Здесь А — площадь поперечного сечения стержня;
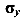 — предел текучести;
— предел текучести;
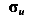 — предел прочности (временное сопротивление).
— предел прочности (временное сопротивление).
Этот метод использовался при расчете строительных конструкций, машин и механизмов до 50-х годов прошлого столетия.
Метод допускаемых напряжений
На смену методу разрушающих нагрузок пришел другой метод -метод допускаемых напряжений. В этом методе ставится требование, чтобы наибольшее напряжение не превышало допускаемого напряжения

Допускаемое напряжение равно опасному напряжению, деленному на коэффициент запаса

Для хрупких материалов опасным напряжением является предел прочности 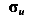 для пластических материалов — предел пластичности
для пластических материалов — предел пластичности 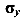 Коэффициент запаса прочности принимается из тех же соображений, что и для метода разрушающих нагрузок.
Коэффициент запаса прочности принимается из тех же соображений, что и для метода разрушающих нагрузок.
Метод предельных состояний
Начиная с 60-лет прошлого столетия, в строительной отрасли при расчете конструкций перешли к более детальному методу — методу предельных состояний. Этот метод учитывает каждый фактор воздействия на сооружение в отдельности. Прежде всего следует объяснить, что такое предельное состояние.
Предельным состоянием называется такое состояние конструкции, при котором она перестает удовлетворять заданным эксплуатационным требованиям.
Целью этого метода является не допустить предельных состояний при эксплуатации и возведении сооружений. В нормах предельные состояния делятся на две группы:
- По потере несущей способности.
- По непригодности к нормальной эксплуатации вследствие недопустимых перемещений, колебаний и трещин.
Условие прочности имеет вид

Здесь R — расчетное сопротивление материала (сопротивление, принимаемое при расчете данной конструкции). Расчетное сопротивление равно

где R» — нормативное сопротивление материала, устанавливаемое нормами проектирования (R» может быть равно пределу прочности 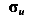 или пределу текучести
или пределу текучести 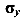 );
);
К — коэффициент безопасности по материалу, устанавливается нормами проектирования и принимается не менее 1,0);
N— расчетное усилие, определяемое при расчете сооружений
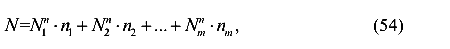
где 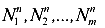 — внутренние силы, возникающие в элементах конструкции от различных видов нормативных нагрузок — собственный вес, вес снега, давление ветра и пр.
— внутренние силы, возникающие в элементах конструкции от различных видов нормативных нагрузок — собственный вес, вес снега, давление ветра и пр.
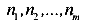 коэффициенты перегрузки, учитывающие случайные отклонения нагрузки от нормативных значений (вследствие изменчивости нагрузки);
коэффициенты перегрузки, учитывающие случайные отклонения нагрузки от нормативных значений (вследствие изменчивости нагрузки);
А — геометрическая характеристика поперечного сечения, соответствующая виду сопротивления элемента (площадь, осевой и полярный моменты сопротивления поперечного сечения).
Возможно эта страница вам будет полезна:
| Онлайн помощь по сопромату |
Геометрические характеристики плоских сечений
Основные понятия и определения геометрических характеристик плоских сечений
Рассмотрим два случая изгиба пластины прямоугольного сечения.
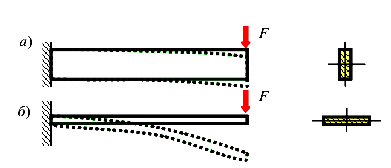
Очевидно, что прогиб в случае (рис.23, б) гораздо больше прогиба в случае (рис.23, а). При этом материал стержней и площадь поперечного сечения в обоих случаях одинаковые, а прогибы разные. Следовательно, площадь сечения не может полностью характеризовать сопротивление стержня изгибу. Поэтому при изгибе, кручении и других видах сопротивления следует использовать иные более сложные геометрические характеристики.
Дадим определения некоторым геометрическим характеристикам плоских поперечных сечений.
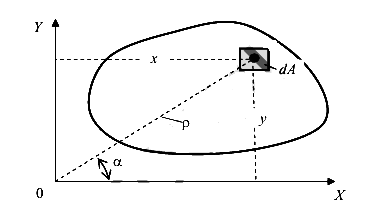
Статическим моментом 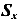 (
(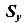 ) плоского сечения относительно оси X(Y) называется геометрическая характеристика равная интегралу
) плоского сечения относительно оси X(Y) называется геометрическая характеристика равная интегралу
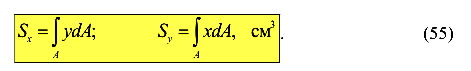
Статический момент может быть равным нулем, меньше или больше нуля.
Центром тяжести плоского сечения является точка, координаты которой вычисляются по формулам
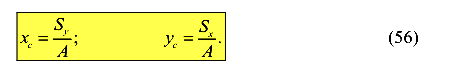
Здесь X, Y- произвольные оси координат.
Отметим, что названые этой очень важной в механике точки имеет ограниченный смысл. Ведь она (эта точка) существует и в том случае, когда тяжести нет. Но отдавая дань всей истории механики, оставим и будем пользоваться этим названием и впоследствии.
Отсюда следует, что статические моменты плоского сечения можно вычислить по формулам

Очень важным выводом является то, что если оси X и Y являются центральными, то координаты центра тяжести сечения равны нулю 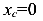 ,
, 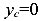 . А это значит, что статические моменты относительно центральных осей всегда равны нулю
. А это значит, что статические моменты относительно центральных осей всегда равны нулю
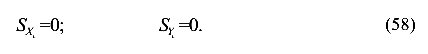
Центр тяжести всегда располагается на оси симметрии, если она имеется у сечения. К такому выводу можно прийти, рассуждая чисто логически. Например, пусть сечение имеет ось симметрии, и центр тяжести лежит не на оси симметрии, а где-то слева или справа от нее. Тогда по законам симметрии такая же точка должна располагаться по другую сторону от оси симметрии. Отсюда следует, что сечение имеет два центра тяжести, что невозможно по условию.
Осевым (экваториальным) моментом инерции сечения называется геометрическая характеристика численно равная интегралу
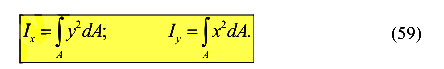
Отметим, что 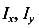 — всегда величина положительная и измеряется в
— всегда величина положительная и измеряется в 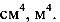
Полярным моментом инерции сечения называется геометрическая характеристика равная интегралу

Полярный момент инерции всегда величина положительная, измеряется в 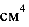 ,
, 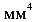 .
.
Между полярными координатами и декартовыми координатами существует связь

Подставим зависимость (61) в выражение для полярного момента инерции (60)
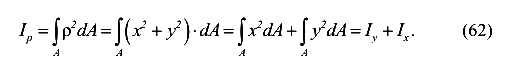
To есть, имеем связь полярного и осевых моментов инерции при условии, что оси X и Y взаимноперпендикулярные, а полюс расположен в точке пересечения этих осей

Центробежным моментом инерции сечения геометрическая характеристика равная интегралу

Центробежный момент инерции может быть положительным, отрицательным или равным нулю, а измеряется в 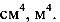 и пр.
и пр.
Зависимость между моментами инерции относительно параллельных осей
Пусть для сечения произвольной формы (рис.25) заданы значения А,  и известно положение центра тяжести. Требуется найти (выразить) моменты инерции этого сечения относительно осей
и известно положение центра тяжести. Требуется найти (выразить) моменты инерции этого сечения относительно осей  ,
,  , проведенных параллельно осям Х, У на расстоянии, соответственно,
, проведенных параллельно осям Х, У на расстоянии, соответственно,  и
и  .
.
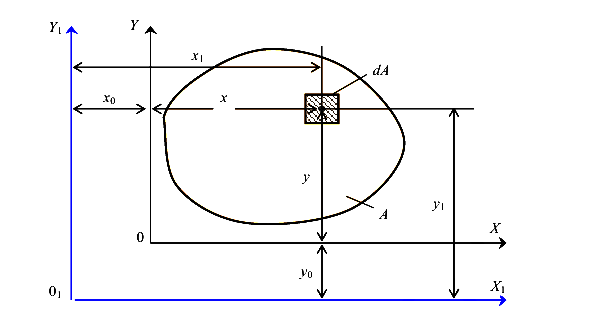
координатных осей
Очевидно, что между координатами выделенной точки существует связь
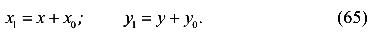
Найдем моменты инерции сечения относительно осей 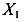 и
и 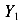
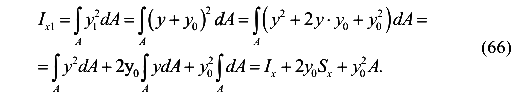
Аналогично для момента инерции 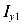 . Найдем связь для центробежных моментов инерции
. Найдем связь для центробежных моментов инерции
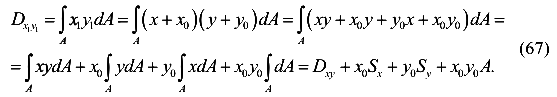
Окончательно имеем
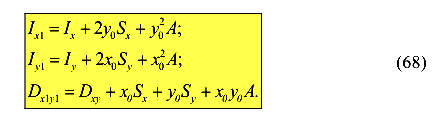
Пусть оси X и Y будут центральными. Тогда статические моменты сечения относительно этих осей будут равны нулю 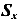 =0 ,
=0 , 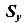 =0. Зависимости между моментами инерции (75) в этом случае упрощаются и принимают вид
=0. Зависимости между моментами инерции (75) в этом случае упрощаются и принимают вид
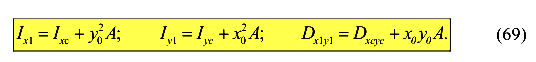
Здесь 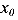 и
и 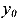 являются расстояниями между соответствующими осями координат
являются расстояниями между соответствующими осями координат  и
и 
Из полученных зависимостей можно выразить моменты инерции сечения относительно центральных осей координат.
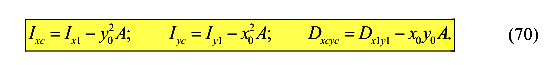
Очевидно, что осевой момент инерции относительно центральной оси всегда меньше осевого момента инерции относительно любой нецентральной оси параллельной центральной.
Возможно эта страница вам будет полезна:
| Сборник задач по сопротивлению материалов |
Моменты инерции сечений простых геометрических форм
Наиболее часто употребляемые формы сечений элементов конструкций являются сечения прямоугольной, треугольной и круглой форм.
Получим формулы для определения моментов инерции сечения прямоугольной формы (рис.26, а)
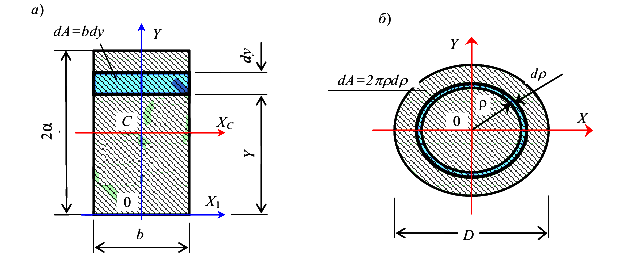
Согласно определению (66) выразим момент инерции относительно оси 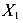
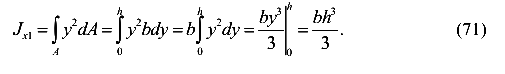
Таким образом, момент инерции прямоугольного сечения относительно оси, проходящей через его основание, равен

Получим формулу для момента инерции прямоугольного сечения относительно центральной оси, параллельной его основанию. Для этого используем зависимость моментов инерции относительно параллельных осей (76).
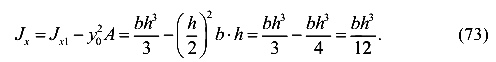
Окончательно имеем

В формулах (72) и (74) в куб возводится размер той стороны, которая перпендикулярна оси, относительно которой вычисляется момент инерции.
Получим формулы для вычисления моментов инерции сечения круглой формы (рис.26, б)
В качестве элементарной площадки здесь удобно выбрать кольцо толщиной равной дифференциалу dр. Тогда полярный момент инерции равен по определению (67)
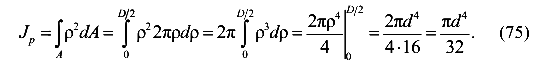
Окончательно имеем

Выведем формулу для вычисления осевого момента инерции круглого сечения, используя ранее полученные зависимости между полярным и осевыми моментами инерции (70),
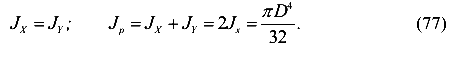
Отсюда следует, что осевой момент инерции сечения круглого сечения равен

Получим формулы для вычисления моментов инерции сечения треугольной формы (рис.27)
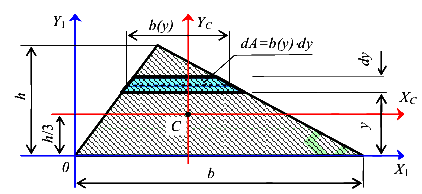
Ширина элементарной полоски меняется в зависимости от ее положения, то есть является функцией от у.

Проверим, так ли это при
при у=0, 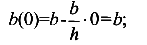
при y=h, 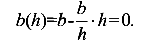
Очевидно, что выбранная функция подходит. Момент инерции относительно оси 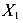 равен
равен
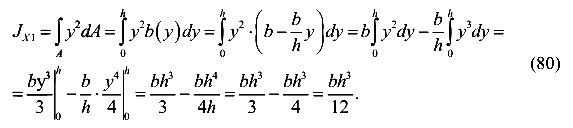
Окончательно имеем формулу для вычисления момента инерции треугольного сечения относительно оси, проходящей через его основание.

Используя зависимость моментов инерции относительно параллельных осей (70), получим
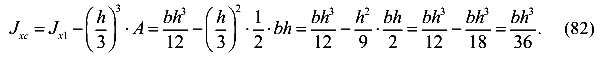
Окончательно имеем

Обратим внимание, что ось 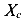 является центральной осью, параллельной основанию треугольника.
является центральной осью, параллельной основанию треугольника.
Зависимость моментов инерции при повороте осей
Пусть для сечения произвольной формы (рис.28) известны 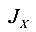 ,
,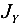 ,
,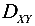 и А. Требуется выразить моменты инерции сечения относительно осей
и А. Требуется выразить моменты инерции сечения относительно осей 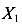 и
и  , повернутых по отношению к осям Х , Y на угол
, повернутых по отношению к осям Х , Y на угол  . Отметим, что оси Х и У могут быть и не центральными
. Отметим, что оси Х и У могут быть и не центральными
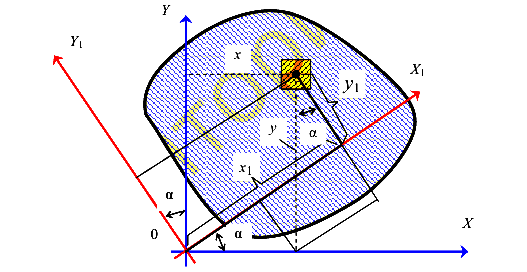
координатных осей
Связь между координатами двух систем координатных осей установим по рисунку 28.
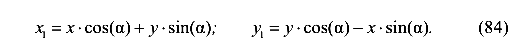
Осевой момент инерции относительно оси 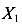 равен
равен
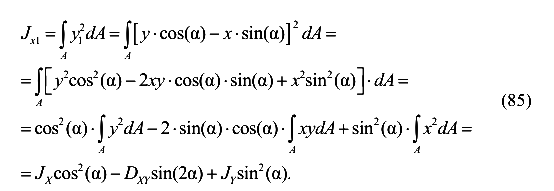
Аналогично получим выражение для момента инерции относительно оси 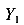 ,
,
Центробежный момент инерции сечения относительно осей 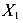 и
и 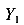 равен
равен
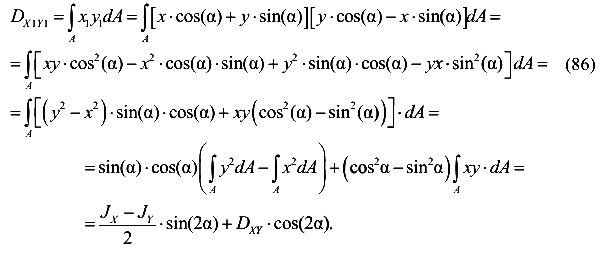
Окончательно имеем
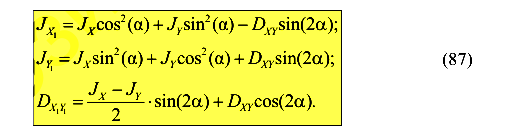
Сложим моменты инерции относительно произвольных взаимно перпендикулярных осей 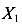 и
и 
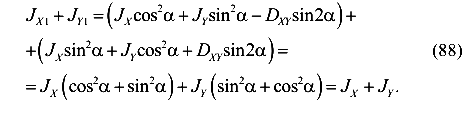
Таким образом, выражение (88) подтверждает, что сумма моментов инерции относительно любой пары взаимно перпендикулярных осей, пересекающихся в одной и той же точке (не обязательно в центре тяжести сечения), является величиной постоянной и равной полярному моменту сечения относительно точки пересечения этих осей.
Главные оси и главные моменты инерции
Рассмотрим сечение произвольной формы. Пусть оси поворачиваю-тся около неподвижной точки С (рис.29)
При изменении угла а изменяются и моменты инерции сечения относительно поворачивающихся осей. Так как моменты инерции выражаются непрерывными функциями (94) с аргументом 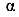 , то они должны иметь экстремальные значения. Обозначим оси, относительно которых моменты инерции принимают экстремальные значения буквами U и V. Причем условимся — ось с максимальным моментом инерции обозначать буквой U, а ось с минимальным моментом инерции буквой V. Найдем положение этих осей, то есть угол
, то они должны иметь экстремальные значения. Обозначим оси, относительно которых моменты инерции принимают экстремальные значения буквами U и V. Причем условимся — ось с максимальным моментом инерции обозначать буквой U, а ось с минимальным моментом инерции буквой V. Найдем положение этих осей, то есть угол 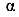
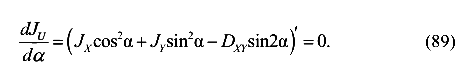
Отсюда получим уравнение
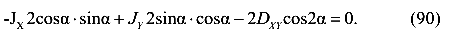
Преобразуем и получим
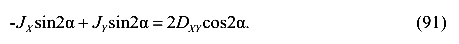
Разделим на 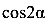 и получим
и получим
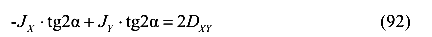
или
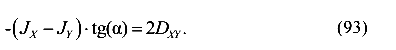
Отсюда получаем формулу для определения положения двух взаимно перпендикулярных осей, относительно одной из которых момент инерции принимает максимальное значение, а относительно другой — минимальное.

Покажем, что центробежный момент относительно этих осей равен нулю. Для этого найдем угол поворота осей, относительно которых центробежный момент становится равным нулю.
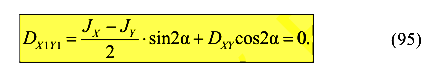
Разделим уравнение (95) на 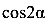 на
на 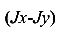 и умножим на 2. В результате получим
и умножим на 2. В результате получим
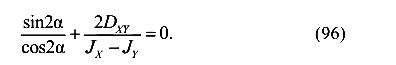
И окончательно получим выражение для угла наклона этих особенных осей инерции по отношению к первоначально взятым осям координат

Очевидно, что угол наклона осей с экстремальными моментами инерции и угол наклона осей, относительно которых центробежный момент инерции равен нулю одинаковые. Следовательно, высказанное предположение справедливо. Дадим название этим особенным осям инерции.
Главными осями инерции называются две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения.
Моменты инерции относительно главных осей называются главными моментами инерции.
Если главные оси проходят через центр тяжести сечения, то они называются главными центральными осями инерции, а моменты относительно этих осей — главными центральными моментами инерции.
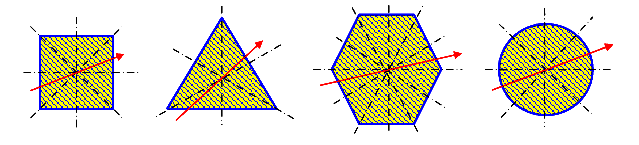
Если сечение имеет ось симметрии, то эта ось и ей перпендикулярная ось, неважно является ли она сама осью симметрии или нет, будут главными осями инерции.
Если сечение имеет более чем две оси симметрии, то согласно определению, любая центральная ось является главной центральной осью инерции. Примеры приведены на рисунке 30.
Главные моменты инерции плоского поперечного сечения вычисляются по формуле (без вывода)
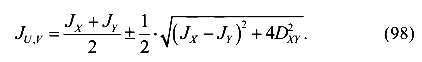
Здесь 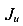 — больший главный момент инерции;
— больший главный момент инерции; 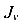 — меньший главный момент инерции, то есть
— меньший главный момент инерции, то есть 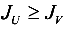 .
.
В некоторых случаях для определения знака или положения объектов удобно использовать правила построения и знаки квадрант координатной плоскости. Отметим, что квадранты образуются разделением координатной плоскости координатными осями на четверти. Квадранты ограничены с двух сторон координатными осями и неограниченны с двух других сторон (рис. 31).
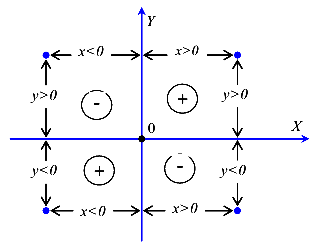
Примем правило расстановки знаков квадрант. Будем считать, что если произведение координат точки величина положительная, то квадрант, в котором расположена эта точка, считается положительным, если произведение координат отрицательное, то квадрант считается отрицательным.
Правило построения главных осей инерции
Ось V с меньшим главным моментом инерции 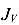 всегда откладываем на угол
всегда откладываем на угол 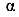 от оси X или Y с меньшим моментом инерции так, чтобы ось V проходила через квадранты, имеющие знак, совпадающий со знаком центробежного момента инерции
от оси X или Y с меньшим моментом инерции так, чтобы ось V проходила через квадранты, имеющие знак, совпадающий со знаком центробежного момента инерции 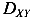 .
.
Очень часто в составных сечениях встречаются элементы в виде равнополочных и неравнополочных уголков. На рисунке 32 показаны положения главных центральных осей инерции V с меньшим главным моментом инерции 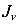 .
.
Центробежный момент инерции прямоугольного треугольника
При поиске положения главных осей инерции и значений главных моментов инерции сечений сложной геометрической формы требуется определять центробежный момент инерции. А для этого требуется знать центробежные моменты инерции частей сечения простых геометрических форм. Для сечений прямоугольного и круглого сечений центробежный момент равен нулю. А вот для сечения треугольной формы его необходимо найти. Рассмотрим сечения в виде прямоугольного треугольника (рис.33).
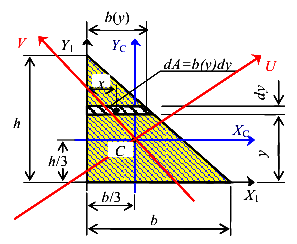
Зависимость ширины элементарной полоски от ее положения, то есть от у, имеет вид

Зависимость координаты центра тяжести элементарной полоски от ее положения, то есть у, имеет вид
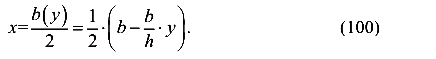
В этом можно убедиться подстановкой у = 0 и у = h. По определению
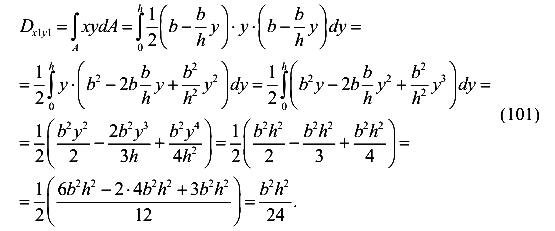
Воспользуемся зависимостью центробежного момента относительно параллельных осей и получим
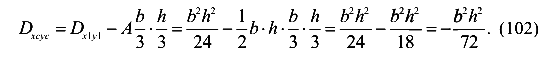
Окончательно имеем формулу для вычисления центробежного момента инерции сечения треугольной формы относительно центральных осей, параллельных катетам треугольника.

Примерное положение главных центральных осей инерции для сечений в виде прямоугольного треугольника показано на рисунке 34.
Возможно эта страница вам будет полезна:
| Учебники по сопротивлению материалов |
Геометрические характеристики сечений сложной формы
Сечения сложной формы делятся на части, имеющие простые геометрические формы — прямоугольники, треугольники, круги и др. К сечениям, имеющим простые формы, относятся те сечения, для которых легко можно указать положение центра тяжести, площадь, значения осевых и центробежного моментов инерции.
Статические моменты и моменты инерции сечения сложной формы вычисляются по формулам
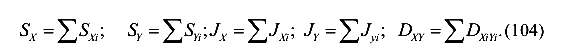
ВНИМАНИЕ. Суммирование статических моментов и моментов инерции относительно разных осей не допускается.
Построение круга инерции
Закон изменения моментов инерции при повороте осей может быть представлен графически в виде круга (окружности) инерции. Координаты каждой точки круга (окружности) инерции равны осевому и центробежному моментам инерции сечения. На самом то деле, мы имеем дело с окружностью, выражающую графическую зависимость осевых и центробежного моментов инерции. Но исторически так сложилось, что эту окружность назвали кругом инерции. Поэтому будем и мы ее так называть.
Круг инерции строится на координатной плоскости, образованной горизонтальной осью, где откладываются значения осевых моментов инерции, и вертикальной осью, на которой откладываются значения центробежных моментов инерции.
В связи с тем, что сейчас в распоряжении инженера имеются достаточно совершенные вычислительные средства, графические методы потеряли свою актуальность, так как и положение главных осей инерции и значения главных моментов инерции можно легко найти по формулам с помощью калькулятора. Однако, мы все равно рассмотрим этот метод, так как он дает нам иллюстрацию к формулам (94) и (98).
ЗАМЕЧАНИЕ. Центр круга инерции всегда расположен на горизонтальной оси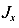 . Круг инерции всегда располагается справа от вертикальной оси
. Круг инерции всегда располагается справа от вертикальной оси 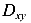 .
.
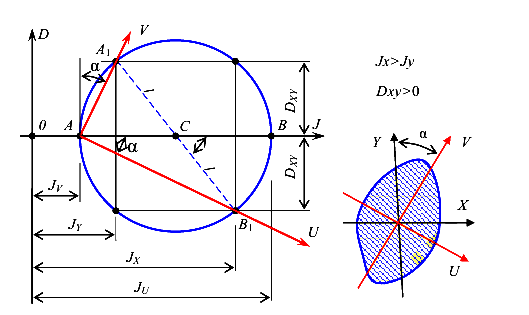
Применение графического метода можно разделить на две задачи -прямую и обратную.
Прямая задача — определение моментов инерции относительно заданной оси, когда известны положения, то есть угол наклона а главных осей инерции к выбранным осям, и значения главных моментов инерции.
Отложим на горизонтальной оси J точки соответствующие значениям 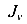 и
и 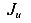 (рис.35). Так как эти точки расположены диаметрально противоположно, то координату центра круга С получим как среднее арифметическое значение величин
(рис.35). Так как эти точки расположены диаметрально противоположно, то координату центра круга С получим как среднее арифметическое значение величин 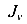 и
и 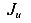 . Нарисуем окружность с центром в точке С с радиусом, равным полуразности значений
. Нарисуем окружность с центром в точке С с радиусом, равным полуразности значений 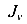 и
и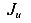 . Из точки А проведем луч X под углом
. Из точки А проведем луч X под углом 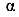 . Координаты точки пересечения луча X и окружности будет являться осевым
. Координаты точки пересечения луча X и окружности будет являться осевым 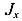 и центробежным
и центробежным 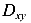 моментами инерции рассматриваемого сечения. Затем под углом 90° проведем второй луч У. Координаты точки пересечения этого луча и окружности будут соответственно равны значениям осевого момента инерции
моментами инерции рассматриваемого сечения. Затем под углом 90° проведем второй луч У. Координаты точки пересечения этого луча и окружности будут соответственно равны значениям осевого момента инерции 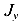 и центробежного момента инерции
и центробежного момента инерции 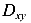
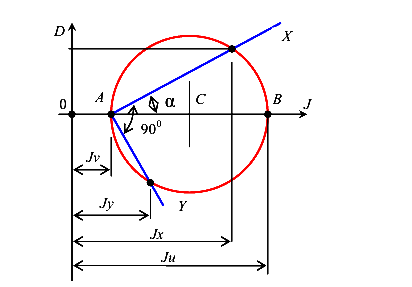
Обратная задача — определение положения главных осей инерции и значения главных моментов инерции поперечного сечения, если известны осевые и центробежный моменты инерции относительно произвольных осей.
Для построения круга инерции отложим на оси J значения момента инерции 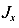 а на оси D значение центробежного момента инерции
а на оси D значение центробежного момента инерции 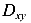 . Используя указанные координаты, нанесем точку
. Используя указанные координаты, нанесем точку 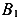 . Затем отложим на оси J значение осевого момента инерции
. Затем отложим на оси J значение осевого момента инерции 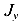 , а на оси D значение центробежного момента инерции
, а на оси D значение центробежного момента инерции 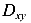 взятого с противоположным знаком и получим точку
взятого с противоположным знаком и получим точку 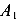 . Построим отрезок
. Построим отрезок 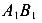 пересечение которого с осью J дает нам центр окружности С. Учитывая, что центр окружности расположен на оси J, найдем его координаты как среднеарифметическое значений величин
пересечение которого с осью J дает нам центр окружности С. Учитывая, что центр окружности расположен на оси J, найдем его координаты как среднеарифметическое значений величин 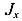 и
и 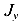 . Радиусом, равным
. Радиусом, равным 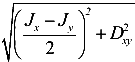 проведем окружность с центром в точке С. В результате получим точки пересечения окружности с горизонтальной осью J — А и В. Координаты этих точек на горизонтальной оси и будут значениями главных моментов инерции
проведем окружность с центром в точке С. В результате получим точки пересечения окружности с горизонтальной осью J — А и В. Координаты этих точек на горизонтальной оси и будут значениями главных моментов инерции 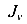 и
и 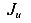 . Направление оси U совпадает с направлением луча, проведенного через точки А и
. Направление оси U совпадает с направлением луча, проведенного через точки А и 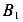 а направление оси Vсовпадает с направлением луча
а направление оси Vсовпадает с направлением луча 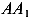
Покажем на рисунке 36, как графическое изображение — круг инерции иллюстрирует формулу (98) для вычисления значений главных моментов инерции. Кстати дополнительная теория из учебников по сопромату тут.
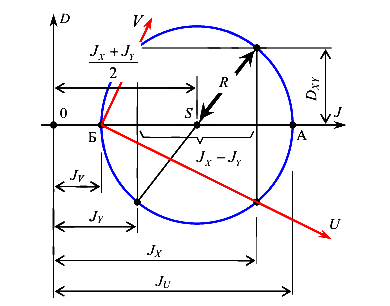
Используя такой же порядок действия, как и при решении обратной задачи, построим круг инерции (рис. 36). Положение центра круга инерции определим как полусумма осевых моментов инерции 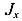 и
и 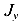

Радиус круга инерции
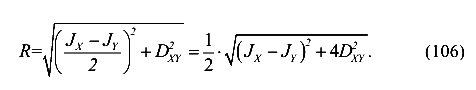
Отсюда следует, что координаты точки А или значение большего главного момента инерции вычисляется по формуле (107)
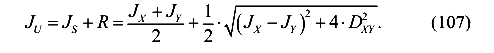
Координата точки Б или значение меньшего главного момента инерции вычисляются по формуле (108)
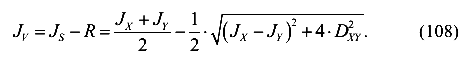
Таким образом, формула (98) графически имеет объяснение.

