Оглавление:












Предиссоциация
- Pre-диссоциация Основные предположения теории, объясненные в этой главе Двухатомные молекулы имеют волновые функции Молекула делится на электронно-волновые продукты Воющая функция (в зависимости от расстояния между ядрами, Параметр) и волновая функция движения ядер.
- Такие предварительно Позиция эквивалентна игнорированию точного Гамильтона. Некоторые молекулы с некоторыми маленькими членами, соответствующими Взаимодействие между ядерным движением и электронами. Учет этих терминов приводит при применении теории Появление переходов между различными электронными устройствами Государство. Кривая потенциальной энергии на рис. 30
Особенно физически важные переходы Между государствами, в которых участвует хотя бы один Для непрерывного спектра. Людмила Фирмаль
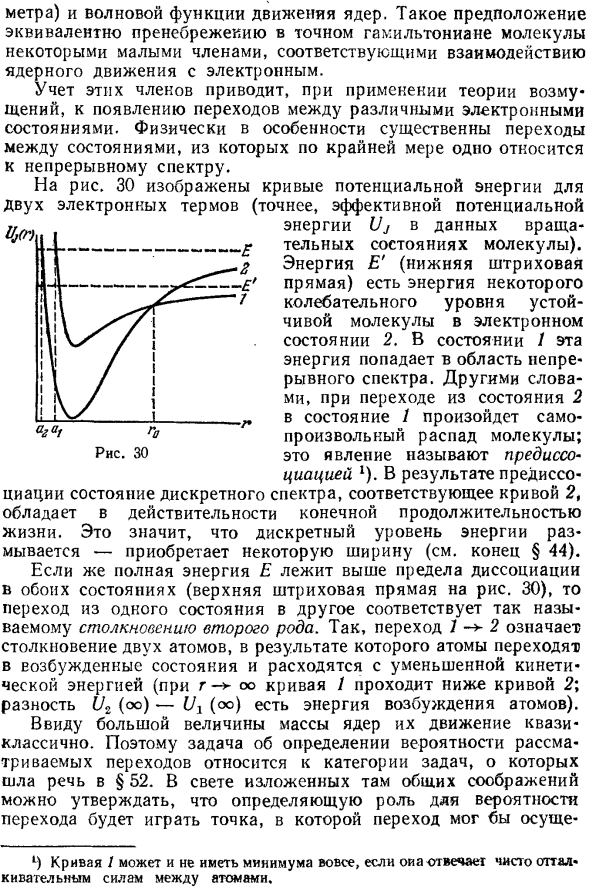
Два электронных термина (точнее, возможные возможности Энергия этих вращательных состояний молекулы Uj). Энергия E f — некоторая энергия Стойкая молекула Л 2. Электронное состояние НИИ 1, эта энергия попадает в область Непрерывный спектр. Другими словами При переходе из состояния 2 в состояние 1 самопроизвольно сломается Молекулы Pad, это явление Рисунок 3 Q1 по диссоциации.
В качестве предварительного результата Состояние дискретного спектра, Соответствует кривой 2 и является на самом деле конечной Ожидаемая продолжительность жизни. Это дискретный х) Если кривая 1 отвечает чисто, не может быть никакого минимума Сила отталкивания между атомами. § 90P R E D I S S O C I A C I Z 421 Уровень энергии эрозии набирает определенный диапазон (См. §44 конец).
Когда полная энергия E превышает предел диссоциации Переход из одного состояния в другое в обоих штатах Соответствует так называемому столкновению типа 2. Таким образом, переход 1 ^ 2 означает столкновение между двумя атомами. В результате атом становится возбужденным Уменьшить кинетическую энергию, чтобы расходиться (г Кривая 1 проходит ниже кривой 2. Разница [/ 2 (0 0) — Ui (oo) Атомная энергия возбуждения).
Из-за большой массы ядер их движение Классический. Поэтому проблема определения вероятности Принадлежит к категории переходных задач Смотри §52. В свете общих соображений, перечисленных там Можно утверждать, что это решающая роль вероятности Переходы воспроизводятся в точках, где возможны переходы 1) классическим способом.
Общая энергия Система двух атомов (молекул) в этом переходе сохраняется Условие «классической выполнимости», которая может быть признана Эффективная потенциальная энергия: Uj \ (r) = Uj 2 (r). Учитывая сохранение полного момента центральной молекулы Поскольку эффективная энергия одинакова в обоих состояниях, Это условие уменьшается, пока потенциальная энергия не станет равной.
Ui (r) = U2 (r), (90,1) Не включает размер момента. Если уравнение (90.1) не имеет реального корня в классе Коммерчески доступные участки (E> U j \, U j 2 зоны) Вероятность перехода согласно §52 экспоненциально мала 2). Пе Переход происходит с большой вероятностью, только если: Кривые потенциальной энергии классически пересекаются Площадь пня (как показано на рисунке 30).
такой Исчезает в случае показателя формулы (52.1) (так Эта формула конечно не применима) Вероятность перехода определяется неэкспоненциальным представлением Время жизни (получено ниже). Условие (90.1) г) Или точка r = 0, где потенциальная энергия = Руки и ноги. 2) Уникальная ситуация возникает в случае миграции с родинками Сотовые термины, которые могут быть реализованы из двух разных пар Состояние атома (см. Конец §85), т. Е.
Кривая потенциальной энергии Как будто расстояние gii разбито на две ветви в направлении увеличения. В таких ситуациях вероятность миграции значительно возрастает. примеров Кто бывает — А. И. Воронин, Е. См. Е. Никитин // Оптика и спектр. 1968. Т. 25. С. 803. 422 D U W X A T O M N A I M O L EK U L A GL. запад В то же время это четко интерпретируется следующим образом: В ОДИ Потенциальная (и полная) энергия одинакова Импульс.
Так что вместо (90,1) G1 = g2, P1 = P2, (90,2) Где р — импульс относительного радиального движения ядра, Индексы 1 и 2 указывают два электронных состояния. Там Так что в момент перехода, Ядерное расстояние и импульс не меняются (так называемый Принцип Фрэнка Кондона). Физически это Скорость электрона лучше ядра В ядре «электронного перехода» нет заметного времени Изменить положение и скорость.
- Установить правила выбора рас не сложно Отображаемый переход. Во-первых, два очевидных Точные правила. Не меняйте пол во время миграции Момент J и знак (положительный или отрицательный, См. § 8 6) терминологии. Прямо из того, что это след Совершенные моменты и свойства волновой функции Отношение инверсии системы координат — точное Конус системы замкнутых частиц.
Кроме того, правила, запрещающие очень точно Переход между переходами (молекулы одного и того же атома) Различные паритетные состояния. На самом деле, паритет Это явление однозначно определяется ядерными спинами и терминологией. Однако сохранение термина символов является строгим законом, и ядерный спин.
Очень точно сохранился благодаря взаимной слабости Действие с электронами. Людмила Фирмаль
Требования к пересечению потенциальной кривой Энергия означает, что термин должен быть другим Симметрия (см. § 79). Рассмотрим существующую миграцию Первое приближение теории возмущений (вероятность Движения, которые происходят в более высоких приближениях л). Гамильтонов термин Приводит к рассматриваемому переходу — вот и все Удвойте уровень.
Среди них Все члены, представляющие спин-орбитальное взаимодействие. Они Является произведением двух осевых векторов из У одного из них есть свойства вращения (то есть, Оператор электронного спина), остальные координаты. ниже Обратите внимание, однако, что эти векторы ни в коем случае не просты Векторы S и L.
Следовательно, он имеет ненулевой штейн. Ключевые элементы перехода, где S ‘и A меняются 0, ± 1 В то же время, если A S = AL = 0 (и Лф0), В этом случае тер симметрия Ма во время миграции вообще не изменилась. Две миграции goy-E-term (осевой вектор имеет матричные элементы См. §87 только для переходов между E + и E_.
Гамильтоновы члены, соответствующие взаимодействиям Вращение, пропорция молекул с орбитальным импульсом Лен Его матричный элемент ненулевой для повторного Spin (двигаться с AL = ± 1 без изменения матричных элементов Если AL = 0, вектор (только ^ -компонентный, т.е. L q По диагонали в зависимости от электронного состояния).
До сих пор с членами считается В результате оператор кинетической энергии ядра (Дифференцирование с ядерными координатами) не только в силе В дополнение к ядерным волновым функциям, электронные функции Зависит от r в качестве параметра. Связанные члены В гамильтониане он имеет ту же симметрию, что и не возмущен Гамильтониан.
Поэтому они могут привести к Перемещаться между электронными терминами с одинаковой симметрией, Поскольку пересечения нет, вероятность ничтожна Срок действия. Перейдем к конкретному расчету вероятности перехода Да я объясню второе столкновение для ясности Какой-то город.
Согласно общей формуле (43.1), требуемая вероятность Определяется выражением Где х яд = rfp — волновая функция радиального движения Ядро), V (r) — энергия интерференции (как величина Vf) Выберите энергию E в (43.1), Ее). Финальная волновая функция Hyad2 должна быть нормальной 5 функций энергии. Нормализация, как это Квазиклассическая функция (47.5) имеет вид Электронные термины возможны, когда один из них является электронным термином.
90.3 Hyad2 (90,1) (Коэффициент нормализации определяется в соответствии с указанными правилами § 2 последний му 1). Начальная волновая функция 424 D U V H A T O M N A I M O L EK U L A GL. запад Написать в форме Хая1 = ггС ° 8 {1 / P l d T ~ 4 I ‘(9 0’ 5) «CL1 Нормализовано, чтобы быть равным единице Плотность магнитного потока каждой из двух бегущих волн Стоячая волна разрешает (90,5); v \ и v ^ — лучевые скорости Относительное движение ядра.
Если вы хотите заменить эти функции (90.3) получает безразмерную вероятность перехода w. Это можно рассматривать как вероятность двух переходов Точка r = th (многопроходное ядро в точке пересечения) Уровень); несколько волновых функций (90,5) В некотором смысле соответствует этому двойному проходу Точка для включения как падения и отражения Бегущие волны.
Матричный элемент V (r) вычисляется с использованием функции Термины (90.4), (90.5), включенные в состав Оценка косинуса, которая может быть разбита на косинусы Сумма и разница аргументов. При объединении вокруг точек ki r = go, значим только второй косинус, поэтому 7G 4 W ~ P2 (Г г \ S n i r ~ l S 1 / затем 1 CL2 Интеграл быстро сходится при выходе из пересечения Ния.
Таким образом, вы можете расширить косинус аргументы в градусах £ = r- интеграция за пределы d £ в следующем диапазоне — От + к (заменяет медленно меняющиеся кратные Тело с косинусом со значением при r = r. С учетом Пересечение р \ = р 2, f p i d r-j K dr »S„ + аи а, 2 Где So — значение интегральной разности в точке r = r. производство Импульс воды может быть выражен как сила F = -DU / др.
Производная уравнения p \ / 2 (i + U \ = p ^ / ^ fi + U2 (^ — Масса данного ядра), dpi dp2 _ 7-r t-r Vi ——- V2 ~ —r \ -G2- доктор д Вот так грамм J P i d r-J p 2 dr w Sq + Fl 2 vF4 2 а я CL2 (V — сумма v \ и v2 на пересечении). Integrova Процедура выполняется с использованием известного выражения + оо J cos (a + β £ 2) d £ = y ^ cos (a + ^), — О И в результате S7TV2 2 f S o 7r \ / n n «\ w = ———— c o s —— h-. (90.6) HV \ F2-Fi | \ N 4U V J Sq / H большое и быстро меняется с изменением Энергия Э.
Поэтому маленький Квадрат космического косинуса энергии можно заменить его средним Значение. Результатом является выражение 4tg1 / 2 W = —-; ————— Hv | F2-Fi j {JI. Д. Ландау, 1932). Все величины справа от уравнения Раскопки на пересечении кривых потенциальной энергии. Интересует вероятность, применительно к предварительной диссоциации Коллапс молекул в единицах времени.
За единицу времени 2 • oi / 2 тг проходит, когда ядро изменяется во время вибрации Точка r = r0, поэтому вероятность предварительной диссоциации Умножить на w (вероятность двойного прохождения) А / 2 тр, т.е. равно __ 2 В Hvif2 Для расчета нужно Следующее замечание. Говоря об общих терминах, Учитывая «невозмущенные» собственные значения Гамильтона Однако движение электрона в молекуле Введен термин V, который приводит к рассматриваемому переходу.
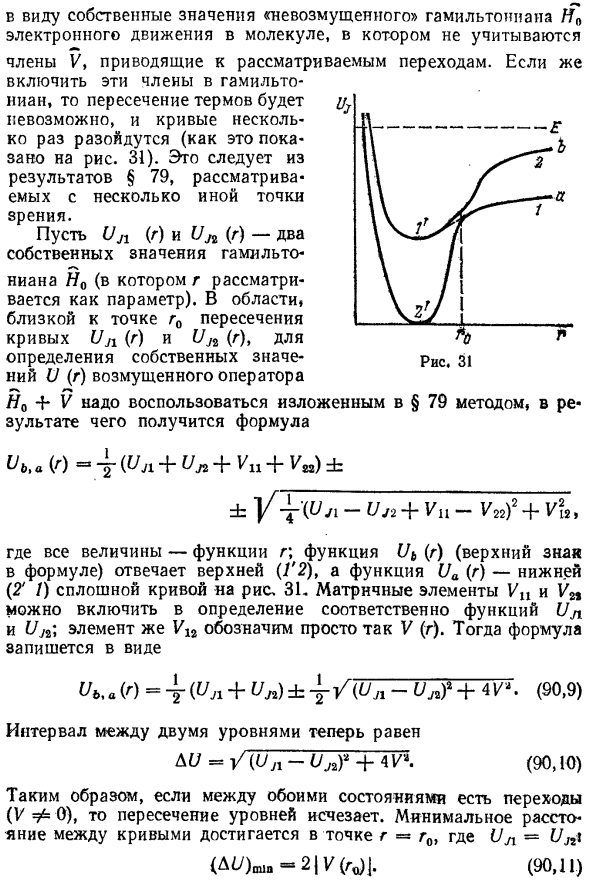
Когда эти термины включены в гамильтониан, Термин невозможен и кривая отделяется несколько раз (Как показано на фиг. 31). Это основано на результатах §79. Рассматривается с несколько иной точки зрения. (90,8) (90,7) 426 D U V H A T O M N A I M O L EK U L A GL. запад Пусть Uji (r) и UJ2 (Y) два собственных значения Гамильтона nian H0 (r считается параметром).
В регионе Вблизи пересечения кривой Uj \ [r) и C / j2 (r), E Определение собственного значения U (г) Мне нужно восстановить оператор возмущения H $ + V Используйте метод, описанный в § 79. И стать выражением Ub, a (r) = \ φn + Uj 2 + Vu + V22) ± ± -Uj 2 + Vu-V2 2) 2 + V? 2 Где все величины являются функциями от r. функция Ub (r) (символ в верхней части выражения) соответствует вершине (I 7 2) и функции Ua (r) -Нижняя часть рисунка (2’1) Сплошная кривая 31.
Матрич Элементы Vu и V2 2 могут быть включены в определение Для функций Uji и [7/2 элемент Vi2 просто обозначен V [r). Тогда выражение записывается в виде Ub, a (r) = \ {U n + Uj2) ± \ V (U j i-U j 2) 2 + 4V2. (90,9) Расстояние между двумя уровнями теперь равно l u = y / (u l до Uj 2) 2 + 4 V 2. (90.10) Так что, если есть переход между обоими состояниями (V f 0) пересечение уровня исчезает.
Минимальное расстояние Разница кривых достигается в точке r = r. Где Uj = V3 2 ‘- (AU) Min = 2 \ V (r0) . (90.11) Вблизи этой точки разница Uj \ -Uj 2 равна Штраф с небольшой разницей Uj 1-U j 2 = Ul-U 2 до {i (Fl-F l), Где F = — (dV / dr) ro. тогда A U = y / (F2-F ) 2 ^ 2 + 4F2 (r0). (90.12) О справедливости полученных формул (90.11) и (90.12) Маленькие (AC /) минуты, если рассматриваются только два состояния Сравните с расстоянием до других терминов.
юстиция Выполнение требуется для формулы вероятности перехода (90,7) Следующие условия (90.19), вообще говоря, более строго Go. Если это условие не выполняется, оно все еще приемлемо Рассмотрим только два условия, но, вероятно, рассчитать Для переходов нормальная теория возмущений неприменима. такой В этом случае требуется более общее рассмотрение.
Ограничиться возле перекрестка, Может быть измерен путем измерения движения ядра полуклассическим способом Системная гамильтонова нить y и координата i являются функциями времени и определяются Это называется классическим уравнением dr / dt = v, т. Е. £ = r-rq = vt. После этого проблема расчета вероятности перехода уменьшается Решить электронное волновое уравнение Функции с нестационарными гамильтонианами: m ^ = [H0 (t) + v (t)] *. (90.13)
Ветхий Завет Соответствующие φ и φ волновой функции электронного состояния Соответствует кривым a и ft. Они являются решениями уравнений (Но + V) lpafi = Ua, b (t) i> a, b, Где т служит параметром. Решение уравнения (90.13) Посмотреть в форме Ф = а (б) фа + б (т) ИПБ (90,14) Решение уравнения с граничными условиями a = 1 и ft = 0 t-) ► — oc, затем | b (oc) | Когда ядро проходит точку r = r, числитель Постоянный φ, что означает переход от кривой а к кривой фут.
анальный Естественно, что | a (os) | 2 = 1- | b (a) | 2 молекулы могут оставаться А на кривой. Переход от кривой А к кривой Ф в двойном Проход через точку перемещения (при приближении и после) Ядерная циркуляция может осуществляться двумя способами: -) ►ft-) ►ft (При приближении происходит переход 1-) ►I 7, В случае расхождения числитель остается на кривой 1’2). a-) ►a-) ►b (1 2 f при приближении, 2 f-) при отклонении ►2).
Следовательно, желаемая вероятность такого перехода w = 2 | b (os) | 2 1- | b (os) | 2 (Здесь рассматривается вероятность перехода при прохождении через точку R-U Go, очевидно, не зависит от направления движения). Значение ft (os) может быть определено, как описано в §53.
Бомба, не полагаясь непосредственно на уравнение (90.13) d). X) В §53 каждый процесс предполагался полностью адиабатическим Причина, по которой вероятность была найдена экспоненциально мала. здесь В этом случае это условие может быть нарушено при прохождении ядра напрямую Близость точки r (когда скорость v недостаточно мала).
Od Однако из выводов, изложенных в §52 и 53, ясно, что применимо следующее: Изоляция для больших \ t \ и возможность только метода Ограничено только двумя уровнями системы. 428 D U W X A T O M N A I M O L EK U L A GL. запад По этой причине вы заметите, что кривые Ua (t) и Ub (t) пересекаются. В воображаемой точке D ±) (90,16) \ F2-Fi \ v Если абсолютное значение отрицательного значения велико т, коэффициент а (т) (90,14).
Время просмотра Г т х дт Далее двигаемся от левой реальной полуоси плоскости Комплексная переменная t к правой полуоси вдоль линии контура «Квазиклассические» условия рома встречаются повсеместно. с того времени Если Ua <Ub, переход должен происходить в верхней половине полосы Кость, которая обходит точку (ср. § 53).
После обхода функции а (т) Перейти к б (т) | B (a) | 2 = exp <-lm -GTO 11 J Ua (t) dt + Jllb (t) d t ^ 1 гто = e x p i-f i I m GTO H J A U dt, Где вы можете выбрать любую точку на действительном числе как т \ Ось, например, t \ = 0. Согласно (90.12), A U = y / (F2-Fi) 2 v 2 t 2 + 4 V2 И требуемый интеграл (с помощью замены t = rm) Перейти я j ^ 4 V 2- (F2-F ) 2v 2t 2 др = я (90.17) n V 2 Я Fa-F я |
Так что в конце вы найдете Вероятность перехода: w = 2 exp 2ttV 2 hv \ F2-Fi | -e x p (—hv \ F2-Fi | (90.18) (C. Zener, 1932). Вероятность перехода Маленький в обоих предельных случаях. Когда V 2 HV \ F2-Fi \ ее Экспоненциально маленький (если адиабатический), и V 2 <hv \ F2-Fi | (90,19) Выражение (90.18) становится (90.7). (90,17), м ^ | V | / 1F2-Fi \ v — это «время ядерного транзита» после точки Пересечение, соответствующая частота iot ~ 1 / т.
Следовательно, оса Появление двух показанных случаев ограничения определяется Связь между Nit и характеристической энергией задачи. Наконец, давайте подробнее рассмотрим соответствующую предиссоциацию. Так называемые возмущения в двухатомном молярном спектре. Два крутых молекулярных уровня Ei и E 2 Поддерживает два электронных термина, которые пересекаются Потенциал друг друга и переход между Элеком Трон ведет к сдвигу уровня.
По словам Общая формула теории возмущений (79.4) Уровень выражения Где V \ 2yad — матричный элемент возмущения для перехода между Молекулярные состояния 1 и 2 (матричные элементы ^ Span и U22yad, очевидно, должны быть включены в E1 и E2. от Эта формула показывает, что оба уровня удаляются и сдвигаются Противоположное направление (по мере увеличения более высоких уровней, Меньше будет уменьшаться).
Размер расширения большой Чем меньше разница, \ E \ -E 2 1. Матричный элемент V \ 2aa рассчитывается точно так: Это было сделано выше при определении вероятности столкновения Второй вид феномена. Разница лишь в том, что корова Новые функции Hyad1 и Hyad2 принадлежат дискретному спектру, Поэтому их нужно нормализовать до единства.
Согласно (48.3) У нас есть И то же самое для x яд2 — сравнение с формулой (90,3) — (90,5) Матричные элементы мент Y \ 2yad связан с вероятностью перехода w в два раза. Передать пересечение по отношению Ei + E2 2: яд | 2, (90,20) (90.21) 430 D U W X A T O M N A I M O L EK U L A GL. запад Z a z h 1. Определите полное поперечное сечение второго типа столкновения как функцию Из кинетической энергии E атома столкновения перехода Взаимодействие ny и спиновых орбиталей [Л. Д. Ландау, 1932).
Может быть введен с учетом квазиклассического движения ядра решения Понятие расстояния столкновения p (расстояние, пройденное ядром) Если между ними нет взаимодействия, они будут проходить друг друга) Разделив площадь поперечного сечения da на вероятность, как произведение площади удара 2npdp Переход w (p) в одном столкновении (ср. I, §18).
Весь раздел Получено интегрированием по р. Для спин-орбитального взаимодействия матричный элемент V (r) независим С момента импульса М сталкивающихся атомов. Скорость записи v Точка r = пересечение кривых в виде K e — „- M. L \ = J i (e — £ e ‘/ 1 \ ЕU 2, “•}) ВДЯУ РС Где U — сумма d и ft на пересечении, а p уменьшается Атомная масса и момент M = ppvoo (voo — относительная скорость атома На бесконечности).
Энергетической точкой отсчета является энергия Начальные состояния атомных взаимодействий были бесконечно нулевыми Глупости; E = p v ^ / 2. Подставляя (90.7) 8tg2! / 2 pdp да = 2 тр дп fi | F2 “Fl1 1 2 (E _ и _ 1 F Интегрирование по дп должно выполняться в диапазоне от нуля до значения Скорость v исчезает. В результате _ 4 года / 2 года Джин 2V 2r 20 с j E-U fi | F2-F i | E 2.
То же самое верно для переходов, связанных с взаимодействиями вращения молей Класс с орбитальным импульсом [Л. Д. Ландау, 1932). Формат элемента V матрицы решений V (r) = MD / pr 2. Здесь, D (r) — матричный элемент орбитального импульса электрона. Таким же образом Итак, как и в задаче 1, _ 1bU2tg2-P2 (E-U) s / 2 a ~ 3Hh1 / 2 / F2-F i | E 3.
Определить вероятность перехода энергии E, близкую к значению Uj потенциальной энергии на пересечении. Если значение решения E-Uj мало, формула (90.7) не применяется Поскольку скорость ma и ядра v нельзя считать постоянной вблизи точки перехода Поскольку это раздел, его невозможно извлечь из-под интегрального символа.
Сделано в заключении (90,7). Заменить кривые Uji, U j 2 прямыми возле пересечения Uj i = Uj-Fj i £, Uj2 = Uj-Fj2 £, £ = r-ro Волновые функции Khad1 и Khad2 в этой области совпадают с волной Функция одномерного движения в однородном поле (см. § 24).
Рассчитать Удобно проводить расчеты с использованием волновых функций с импульсами Настройка. (5-волновая функция, нормированная на энергетическую функцию, Иметь форму (см. § 24 выпусков) 1 A2 =: опыт y j 2i7T f l \ F j 2 | A I {—I H F j 2hFn (E-U j) p -% — 6 футов. } ■
Функция нормирована на равную единицу плотности магнитного потока при падении Отраженная волна, полученная умножением l / 27gK: И 1 =: exp (.E-U j) p-f v / fF / i | I hFji 6 / i. Интегрируя энергию возмущения (матричные элементы), вы можете: Однако уберите снизу знак интеграла и замените значением балла пересечения: о W = 2 тг V J a \ a2dp В результате 4 Вт V 2 (2 / х) 2/3 n4 / 3 (F j 1F j 2) 1/2 (Fj2-Fj i) 2 / ‘3 x «G- (E-U j) 1/3 P2) \ F J2 Z j t \ f j __ M F j i) 2/3 ‘ (90.22) Где Φ (ξ) — функция Эйри (см. Математическое приложение §b).
мучительный Их E-Uj, эта формула идет к (90.7). 4. Определите вероятность зарядки с гораздо меньшей скоростью (отн. Относительная скорость и C 1) Столкновение между атомом водорода и ионом водорода Йоко (О.Б. Фирсов, 1951) г). Определить H + H + систему как молекулу Ион водорода (см. Проблему в §81).
Перезарядка состоит из электронных переходов Приближенное состояние φ2 из состояния φ1, локализованного в первом ядре Второе ядро. Эти состояния Движущееся ядро; устойчивое состояние Фе, и = — ^ = (ф1 ± ф2). Энергия как функция расстояния R между ядрами: Ug: U (R). отрава Ра совершает указанное медленное движение (это Классическая), эти энергии медленно меняющиеся функции.
Зависимость времени от времени и волновых функций Чувствительные ко времени факторы exp r J Ug, u (t) dt ^ j (См. § 53). Суперпозиция обоих состояний, которые соответствуют ψ при t = —∞ F = V2 T «/ t /) g exp-i Ugdt I + fi exp I —g / Uu dt T ■ / 1) Эта проблема использует атомные единицы. 432 D U V H A T O M N A I M O L EK U L A GL.
запад Для t-oo эта функция представляет собой линейную комбинацию вида C r f r + C2F2, а вероятность перезарядки w = | C2 12- , 2 W = s i n 00 h, v = l j (u u-ug) dt Столкновение р с большим расстоянием столкновения При достаточно низкой скорости v) движение ядра можно рассматривать как прямое Линейный, т. Е.
Разница для R = \ / p2 + v 2t2 равна Ug от U-R 1 Он задается уравнением (4) из задачи в §81. тогда 4 ф R 2e-R ~ 1 l = — (IR. V J ^ / R 2- р Для интеграла p »1 область значений R близка ко дну Предел; настройка R = p (1 + x) о _ 2 ^ 2 2-р (е ~ р х Дж 2 / 27г 3 / а n ~ —— p с I ——- даже = ——— p ‘e.
Смотрите также:
| Λ -удвоение | Преобразования симметрии |
| Взаимодействие атомов на далеких расстояниях | Группы преобразований |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

