Оглавление:

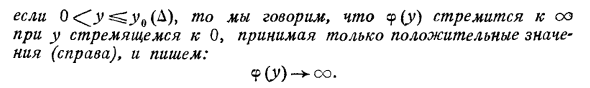

Пределы при x стремящемся к 0
- Ограничение по л. Есть тенденция к 0. Пусть 9 (x) — функция от x,lim 9 (a 🙂 = / и> = — ~. Put С х-л Когда х имеет тенденцию быть со, у стремится к пределу 0 и стремится к пределу /. Здесь мы удалим x из рассмотрения и предположим, что ty (y) является функцией от y. Только большие положительные значения x, то есть значения y, соответствующие небольшим положительным значениям y, обрабатываются.
Точнее, это предложение можно сформулировать следующим образом: (G 🙂 = / означает, что для любого небольшого положительного числа S вы можете найти x0 как .y (x) — для всех значений x, равных x0 Или равно, но это означает, что вы можете Выберите i = 11 <«o для всех позитивов lg0 Значение у составляет у0 или меньше.
Функция (y) обладает свойством, что, если y достаточно мало, значение может быть изменено с / на любую величину. Людмила Фирмаль
Поэтому определение таково. A. Вы можете найти y0 (8) для любого небольшого положительного числа a. | 900- / | D, Если это 0 (D), y (y) имеет тенденцию быть oo. Когда у становится О и принимает только положительное значение (справа), напишите следующее. 90) — * с.
Точно так же, определите значение фразы: «90>) имеет тенденцию быть ограничением I, что у становится 0 и принимает только отрицательные значения (левая сторона)» или «limqp (Y) = / для y — ** — O «. Для этого просто замените неравенство 0 <^ y в определении A неравенством -y0 (g) ^ y 0. Конечно, есть определение, аналогичное соответствующему аналогу в определении B. 9 вс) — * — 00 Для y-0 или y-co. Если lim 9 (y) = 1 и lim 9 (») = /, просто напишите y- + + o y — * — o lim 9 (y) = /. у-> 0 Этот случай настолько важен, что мы рекомендуем вам создать другое определение.
| Символы | Пределы при х стремящемся к а |
| Пределы при х стремящемся к бесконечности | Монотонно возрастающие или убывающие функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Для любого небольшого положительного числа c, если вы можете найти v0 (S) со всеми значениями ur, отличными от 0, и по модулю, не превышающему y0 (o), значение 9 (y) равно 9 O ‘), который меньше этого, имеет тенденцию становиться пределом I, потому что у становится 0, и записывается следующим образом. lim 9 (y) = 1. Аналогично, если 9- (y) -> co — это y -> — 0 и y-0, скажем, 9 0>) -> co, как y- + 0. Утверждение 9Cv) -> — 00 определяется так же, как γ- + 0. Наконец, 9 (y) колеблется относительно y (ограниченный или неограниченный в зависимости от ситуации), если 9 (y) не имеет тенденцию быть либо конечным пределом, либо никнеймом y + 0 Скажите — ► + (); операторы определяются аналогичным образом. 9 (y) изменяется как y — + — 0y.
Предыдущее определение было сформулировано в терминах переменной, обозначаемой у. Однако ясно, что обозначение переменных не играет никакой роли, и во всех этих определениях можно предположить, что буква y заменена на x.

