Оглавление:



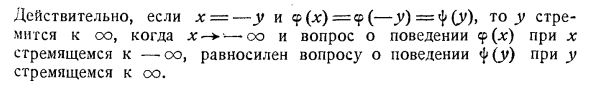
Пределы при х стремящемся к бесконечности
- Предел х, который стремится к co. Далее вернемся к функции непрерывной вещественной переменной. Ограничение только функцией с одним значением, 1) показать такую функцию следующим образом: x принимает все значения, соответствующие точке главной линии A, и начинается в определенной точке этой линии. Предположим, вы всегда двигаетесь вправо. В этих условиях x имеет тенденцию быть бесконечным или со, и записывает x- + oo. Единственная разница между этим «стремлением x к oo» и «стремлением lxco», описанным в предыдущей главе, состоит в том, что x принимает все значения при стремлении к co.
То есть точка P, соответствующая x}, является точкой на прямой A справа от начальной позиции I. С другой стороны, я склонен быть резко бесконечным. Как уже объяснялось в начале предыдущей главы, между функциями x и n существует очень тесная связь. Каждую функцию n можно рассматривать как выбор некоторых значений функции x. В предыдущей главе мы исследовали поведение функции φ (π), где n стремится к ω.
Эта разница показывает, что l: постоянно стремится к oo. Людмила Фирмаль
Здесь мы имеем дело с той же проблемой для функции 9 (^. Определения и теоремы, которые здесь приводятся, по существу являются повторениями соответствующих определений и теорем в предыдущей главе. Следовательно, согласно определению 58 в пункте 58, Определение 1. Функция cp (x 🙂 предназначена для любого небольшого положительного числа I, все значения x равны π0 (S), ср. (Lg)
Это отличается от меня на б, то есть Когда x> x0 (3). В этом случае напишите: Иш 9 (х) = /, L «—► и Или, если вы не можете понять это неправильно, просто lim 9 (x) = / или 9 (x:) — * — /. Точно так же, Определение 2. Функция 9 (x) стремится к нулю с x. Для любого большого числового значения Δ, если мы можем найти числовое значение η: 0 (Δ), 9 (*)> D в Тогда пиши 9 (х) — * оо. Определяется аналогично 9 (n:) — ►— oo1).
| Геометрическая прогрессия 1+f+z++…c комплексным z | Пределы при x стремящемся к 0 |
| Символы | Пределы при х стремящемся к а |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Наконец, есть следующее: Определение 3. Скажем, что 9 (l;) колеблется, потому что x имеет тенденцию быть oo, если не выполняется ни одно из условий в предыдущем определении. В то же время 19 (x) | 9 (x 🙂 колеблется с границей, потому что он остается меньше постоянной K для всех x> x0 * K, в противном случае -9 (x) не имеет границы Говорят, что он будет колебаться. Читатель напоминает, что в предыдущей главе мы подробно рассмотрели различные неформальные выражения утверждения 9 (l) -> f, 9 (l) —►co. Конечно, если вы думаете прямо сейчас, применяется аналогичное выражение.
Слова «маленький», «почти» и «большой» относятся к разделу IV. Пример XXXIV. 1. Рассмотрим поведение следующих функций l: -v s: 1, 1 + 1, X *, X *, IX], x- [x], [X] + V ^ -H ‘Первые четыре функции точно соответствуют функции n. Ч об этом. Внутривенно Последние три функциональных графика были созданы гл. P (ex. XVI. 1, 2, 4), читатели немедленно меняют [l *] — * oo, * — [l *] на ограниченный диапазон, [x] — {- ^ x— [x ] — * оо. Давайте сделаем простое заявление здесь. Функция <$ (x) = x— [x] изменяется от 0 до 1, как вы можете видеть на графике. Поскольку целое число x равно нулю, соответствующая функция (n) всегда равна нулю и поэтому стремится к нулю.
Таким образом, мы можем сказать, что 9 (*) мало, почти равно / или велико, если х велико. Людмила Фирмаль
То же самое относится и к функциям у (. * •) = грех хр. Где
— oo) сопровождается соответствующим свойством <f («), но обратное часто Не правда 2. Рассмотрим функцию таким же образом. -, * Синьжен, (x sin tg.vr, acos2лгп-f ^ sin2 *;: График этих функций показывает результаты обзора. 3. Дайте геометрическое описание определения 1, аналогичное приведенному в разделе 1. IV, стр. 59. 4. <f (x) cos xx, если tp (x -) — v / и / отличны от нуля. И <p (A-) sin.v- вибрировать в ограниченном диапазоне. Если <p (.c) -co или <p (l:) — oo, он будет колебаться бесконечно.
График для каждой из этих функций представляет собой волнистую кривую, которая колеблется между кривыми y = zy (x) и y = -y (x). О программе. Рассмотрим поведение функции x-b-c y = f (x) cos2 dg- + F (x) sin2 xt. , Где f (x *) и F (x) — любые две простые функции (например, xχ2). [График y — это кривая, которая колеблется между кривыми y = / (g). 91. Предел x имеет тенденцию быть -oo. Читатели могут легко сформулировать определение значения выражения «х нацелен на -co» или «x -►-oo» lim qp (x) = 1, φ (;;) — соω, φ (:):) — оо X — * — ооНа самом деле, x = —y и cp (x) =? Когда (-y) = ty (y) t, y стремится к ω. Это эквивалентно проблеме операции ^ (^ y), потому что у стремится стать со.

