Оглавление:
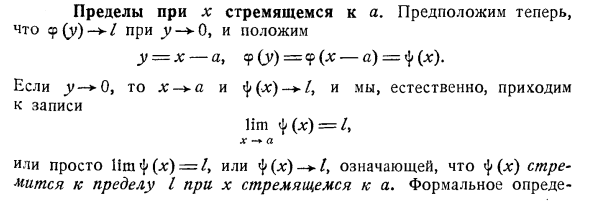

Пределы при х стремящемся к а
- Предел х стремится к. Где .y -> — O y = x-a, cp 0 ‘) = 9- = ΦC ^ — Если y-> 0, запись достигается естественным образом с помощью x- + a и φ (g:) — ► / Lim = х а Или только один! фφ (・ *) = / или ^ (a:) — ► означает, что ty (x) стремится к пределу I при переходе x к a.
- Формальное определение Утверждение для этого утверждения: X- »О Определение утверждения, которое ограничивается значениями x, большими, чем a, то есть неравенство 0 | a: неравенство ax ^ a + e (2), «9 (x;) склонен / Λ: склонен вправо»
Если е (5) может быть дано для любых 8, / | <« 0-а я е (б), то lim 9 (*) = /. Людмила Фирмаль
| Пределы при х стремящемся к бесконечности | Монотонно возрастающие или убывающие функции |
| Пределы при x стремящемся к 0 | Верхний и нижний пределы и принцип сходимости |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Получается. lim 9 (n 🙂 = /. х- * а — \ — о Аналогично, определите отношения lim 9 (jc) = L х-а-О Таким образом, предложение lim 9 (x) = I эквивалентно двум предложениям х а Denia: lim 9 (x) = /, lim 9 (*): = /. * a + O x ~ * a-O
Кроме того, 9 (x;) -> oe или 9 (x) — * — co имеет тенденцию быть a, где x — большое значение, небольшое значение, a, но теперь эти определения объясняются более подробно. Там нет необходимости делать.
Они полностью аналогичны определениям, определенным в особом случае a = 0 выше, установите x-a = y и y-> 0. Людмила Фирмаль

