Предельный переход в неравенствах
Рассмотрим последовательности 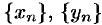 и
и 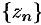 .
.
Теорема 15.1. Если 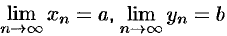 и, начиная с некоторого номера, выполняется неравенство
и, начиная с некоторого номера, выполняется неравенство 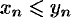 , то
, то 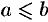 .
.
Допустим, что 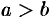 . Из равенств
. Из равенств 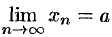 и
и 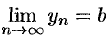 следует, что для любого
следует, что для любого 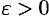 найдется такое натуральное число
найдется такое натуральное число 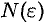 , что при всех
, что при всех 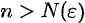 будут выполняться неравенства
будут выполняться неравенства 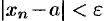 и
и 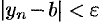 , т. е.
, т. е. 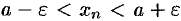 и
и 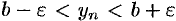 . Возьмем
. Возьмем 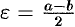 . Тогда:
. Тогда: 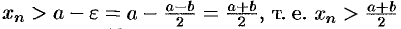 и
и 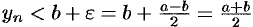 , т. е.
, т. е. 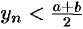 . Отсюда следует, что
. Отсюда следует, что 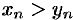 . Это противоречит условию
. Это противоречит условию 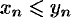 Следовательно,
Следовательно, 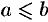 .
.
Теорема 15.2. Если 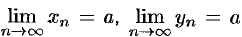 и справедливо неравенство
и справедливо неравенство 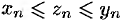 (начиная с некоторого номера), то
(начиная с некоторого номера), то 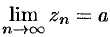 .
.
(Примем без доказательства.)
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Числовые множества |
| Числовые промежутки |
| Предел монотонной ограниченной последовательности |
| Непрерывность функции в точке |

