Предельные точки числового множества. Открытые и замкнутые множества
Множество вещественных чисел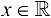 
, удовлетворяющих неравенству 
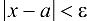, т. е. 
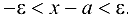, называется 
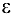-окрестностью точки 
.
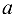Множество вещественных чисел 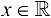, удовлетворяющих неравенству 
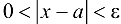, называется проколотой 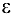-окрестностыо точки 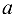(точка 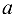исключена из своей 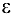-окрестности).
Геометрически 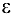-окрестность точки 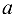есть интервал 
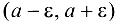длиной 
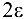, серединой которого является точка 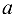числовой прямой.
Точка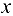 
называется предельной точкой множества X, если в любой 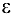-окрестности точки 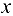находятся точки из X, отличные от 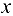. Предельная точка может как принадлежать, так и не принадлежать множеству X.
Точка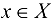 
называется изолированной точкой этого множества, если в достаточно малой ее 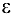-окрестности нет точек из Z, отличных от .
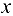Точка 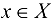называется внутренней, если существует некоторая 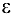-окрестность этой точки, целиком содержащаяся в множестве X.
Множество, все точки которого являются внутренними, называется открытым’, множество, содержащее все свои предельные точки, называется замкнутым. Открытым множеством является, например, интервал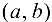 
, замкнутым множеством — отрезок 
.
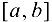Точка 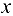называется граничной точкой множества X, если любая 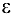-окрестность этой точки содержит точки, как принадлежащие множеству X, так и не принадлежащие ему. Множество всех граничных точек множества X называется границей этого множества. Например, если
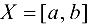, то все точки интервала 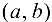являются внутренними точками множества X, а граница этого множества состоит из двух точек: 
.
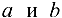Если множество X представляет собой область (открытое множество), то множество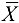 
, полученное присоединением к X всех граничных точек этого множества, называется замкнутой областью.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Логические символы в теории множеств |
| Грани числовых множеств |
| Функция |
| Способы задания функций с примерами |
