Оглавление:
Предел последовательности
а) Число а называется пределом последовательности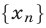 
, если для каждого 
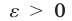существует номер 
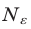такой, что для всех 
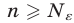выполняется неравенство
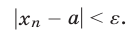
Если а — предел последоват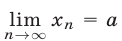
льности 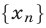, то пишут 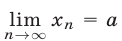или 
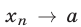при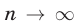 
. Последовательность, имеющая предел, называется сходящейся, а последовательность, не имеющая предела, называется расходящейся.
б) Свойства сходящихся последовательностей.
1°. Если последовательност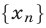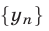и , 
и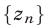 
таковы, что для всех 
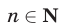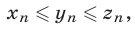
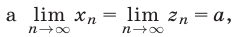справедливо неравенство 
то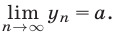 
2°. Если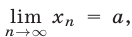 
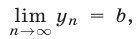то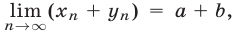 
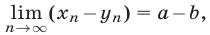
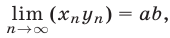
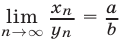(при условии, что 
).
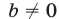в) Примеры сходящихся последовательностей.
1°.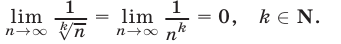 
2°.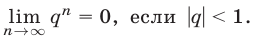 
3°. Если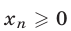 
при всех 
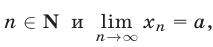то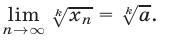 
4°.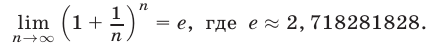 
Пример №33.
Найт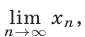и 
если:
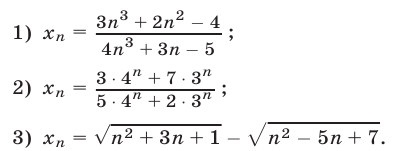
Решение:
1) Разделив числитель и знаменатель дроби на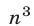 
, получим 
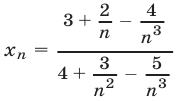. Так как 
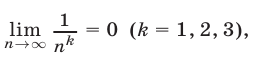то числитель имеет предел, равный 3, а предел знаменателя равен 4. Поэтому 
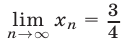в силу свойств пределов.
2) Разделив числитель и знаменатель дроби на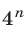 
, получим 
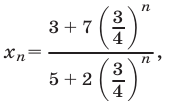откуда следует, что 
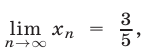так как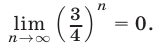 
3) Используя формулу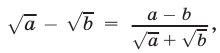 
запишем 
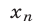в следующем виде 
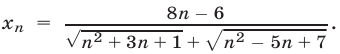Разделив числитель и знаменатель на n, получим 
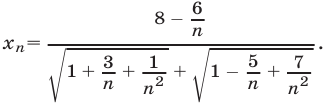Если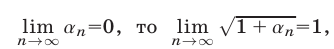 
и поэтому предел знаменателя равен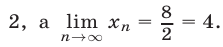 
Ответ.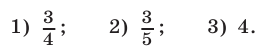 
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
