Предел монотонной ограниченной последовательности. Число e. Натуральные логарифмы
Не всякая последовательность имеет предел. Сформулируем без доказательства признак существования предела последовательности.
Теорема 15.3 (Вейерштрасс). Всякая монотонная ограниченная последовательность имеет предел.
В качестве примера на применение этого признака рассмотрим последовательность 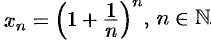 .
.
По формуле бинома Ньютона
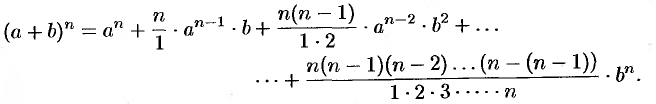
Полагая 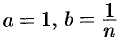 , получим
, получим
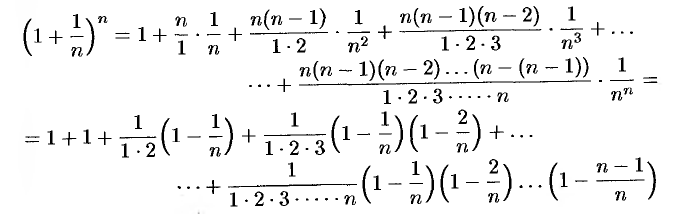
или
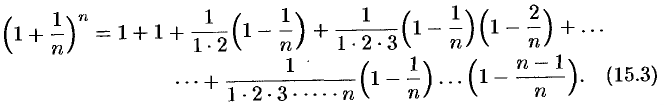
Из равенства (15.3) следует, что с увеличением 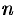 число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении
число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении 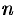 число
число 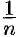 убывает, поэтому величины
убывает, поэтому величины 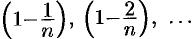 возрастают. Поэтому последовательность
возрастают. Поэтому последовательность 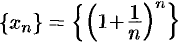 — возрастающая, при этом
— возрастающая, при этом

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства (15.3) на единицу; правая часть увеличится, получим неравенство
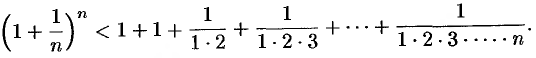
Усилим полученное неравенство, заменив числа 3, 4, 5,…, стоящие в знаменателях дробей, числом 2:
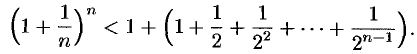
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
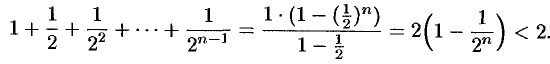
Поэтому
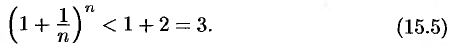
Итак, последовательность ограничена, при этом для 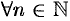 выполняются неравенства (15.4) и (15.5):
выполняются неравенства (15.4) и (15.5):
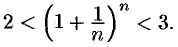
Следовательно, на основании теоремы Вейерштрасса последовательность 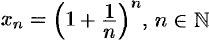 , имеет предел, обозначаемый обычно буквой
, имеет предел, обозначаемый обычно буквой 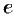 :
:

Число 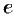 называют неперовым числом. Число
называют неперовым числом. Число 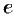 иррациональное, его приближенное значение равно
иррациональное, его приближенное значение равно 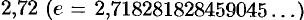 . Число
. Число 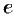 принято за основание натуральных логарифмов: логарифм по основанию
принято за основание натуральных логарифмов: логарифм по основанию 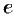 называется натуральным логарифмом и обозначается
называется натуральным логарифмом и обозначается 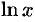 , т. е.
, т. е. 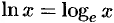 .
.
Найдем связь между натуральным и десятичным логарифмами. По определению логарифма имеем 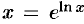 . Прологарифмируем обе части равенства по основанию 10:
. Прологарифмируем обе части равенства по основанию 10:
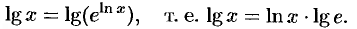
Пользуясь десятичными логарифмами, находим 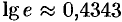 . Значит,
. Значит, 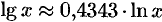 . Из этой формулы следует, что
. Из этой формулы следует, что 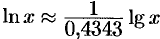 , т.е.
, т.е. 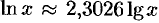 . Полученные формулы дают связь между натуральными и десятичными логарифмами.
. Полученные формулы дают связь между натуральными и десятичными логарифмами.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Числовые промежутки |
| Предельный переход в неравенствах |
| Непрерывность функции в точке |
| Непрерывность функции в интервале и на отрезке |

