Оглавление:

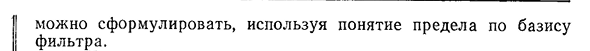

Предел интегральных сумм по базису фильтра
- Предел суммы интегрирования на основе фильтра. Рассмотрим множество всех разделов{x&}в сегменте[a, b]. Обозначим это M *
множество всех возможных разбиений символом P*.
Таким образом, вы получаете отображение на набор интегральных сумм для набора Людмила Фирмаль
разделов. Выберите в P * основу фильтра (base) * B={VA}с элементами= * {{Xfe}eP:d<8}. Эта запись означает, что элемент
B6*является разделом{XY}, диаметр d которого меньше B., Но Здесь предел означает предел числовой функции a (интегральная сумма
- функции f (x)), основанной на фильтре(d- » -0). Из-за свойств базового предела этот предел является единственным пределом. Если диаметр
разбиения стремится к нулю, то все теоремы из предыдущего абзаца, в которых использовался предел суммы,
очевидны..370Ч 9. Очистить Людмила Фирмаль
Интеграл Римана Он может быть сформулирован с использованием концепции ограничений на основе фильтров.
Смотрите также:
Методическое пособие по математическому анализу
| Краткие сведения о комплексных числах | Первый замечательный предел |
| Второе достаточное условие перегиба | Второй замечательный предел |

